Таким образом, если линейная часть системы устойчива, то условия существования субгармонических колебаний принимают вид:

1. Условия надлежащих моментов переключения: ЛГо (v2k - ф) - г, (-) = - / + Ко -f yW (0).

Л/о (Y.v2k - ф) - г, (у, = - f - Ко + г/о^о (0). ]

2. Условия надлежащих направлений переключения:

Лvf(v2л-ф)--jg-vfj (Y,v2n -ф)-z-

\ СОо /

2п

СОо

<0.

(7.280

Кроме того, x{t) не должно иметь дополнительных переключений. Эти условия переключения определяют неизвестные Yi и ф.

Если же линейная часть нейтральна, то условия существования субгармонических колебаний принимают такой вид: 1. Условия надлежащих моментов переключений:

Лfo(v2я -ф) -z,p

СОо

= - fn + 2о + Ко,

(7.29)

(7.290

Afo (у,Г2я - ф) - 22 IYi -j = - /п + Zo -. Ко.

. 2. Условия надлежащих направлений переключения: А^%{2п-)-М-[)>0,

Лvf(Y,2я-ф)-iz7(Y,--)<0.

Кроме того, хЦ) не должно иметь дополнительных переключений. Эти условия переключения определяют неизвестные Zo и ф. Условия существования субгармонических колебаний при V = 1 обращается в уже известные нам условия существования вынужденных колебаний основной частоты.

Глава VIII

ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В РЕЛЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМАХ

§ 8.1. Релейные системы без зоны нечувствительности

При исследовании вынужденных колебаний в релейной системе без зоны нечувствительности частота их соо является заданной величиной, а искомой величиной является сдвиг фаз ф между вынужденными колебаниями и внешним периодическим воздействием. Величина ф должна быть действительной и удовлетворять условиям существования вынужденных колебаний (7.6) и (7.7).

Для фактического определения ф воспользуемся годографом релейной системы, который применялся выше при исследовании автоколебаний.

Введем комплексиозначную функцию

(я - ф) = Л [foin - ф) + По (п - ф)] (8.1)

и рассмотрим сумму этой функции и годографа релейной системы

/ (ш) = Re / (ш) -f л m / ((О) = - (] - jz {), (8.2)

т. е. рассмотрим функцию

(я-ф)-Ь/(со). (8.3)

Мнимая и действительная части этой суммы

Im {S (я - ф) + / (со)} - Лfо (я - ф) - г . Re {{n-) + J (со)} = Afo (я - ф) - k (-j)

(8.4)

при со = СОо тождественны левым частям условий надлежащих моментов переключений и направления переключений (7.6), (7.7).

Следовательно, условия существования вынужденных, колебаний частоты СОо можно представить в форме

1т{32-(я-ф) + /(соо)} = -Ко, I

Ре{5(я-ф) + /(соо)}<0. J -

jlm/(u)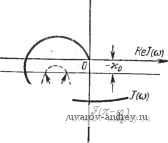

Этим условиям можно придать удобную геометрическую интерпретацию. ,

Изобразим на плоскости J годограф релейной системы и проведем прямую -(рис. 8.1) аналогично тому, как это делалось при исследовании автоколебаний.

Пусть со = СОо есть частота внешнего периодического воздействия. Отметим на годографе /(со) точку со = соо и, выбирая ее в качестве начала координат О', построим кривую, описываемую концом вектора (я -ф) при А - const и изменении ф от О до я*).

Вектор, проведенный из начала координат О к построенной кривой, равен сумме /(со) и (я -фо) при со = СОо. Условия (8.5) будут удовлетворяться лишь для тех значений ф, при которых кривая (п - ср) пере- -Sji.t секает прямую - щ в левой полу- \ о i

плоскости. Значения ф, которые удовлетворяют условиям (8.5), определяются как отметки на кривой {п - ф) в точках пересечения ее с прямой -Ко. лежащих в левой полуплоскости.

Число найденных таким образом значений ф определяет число периодических решений, соответствующих возможным вынужденным колебаниям. Эти вынужденные колебания z{t) отличаются лишь сдвигом фаз.

Рассмотрим влияние изменения величины А на наличие и число возможных вынужденных колебаний, частота которых отлична от частоты автоколебаний. Величина А изменяет масштаб кривой б^(я -ф). При достаточно малых А точка пересечения кривой {л - ф) и прямой -Ко отсутствует (рис. 8.2,а). Это значит, что вынужденные колебания частоты ©о, которые бы подавили автоколебания, отсутствуют, и в системе может иметь место режим биений либо субгармонический режим.

При достаточно больших значениях А появятся точки пересечения кривой (зт -ф) с прямой -Ко (рис. 8.2,6 или в).

Значения ф, которые соответствуют точкам пересечения, лежащим в левой полуплоскости, и определяют соответствующие периодические решения, а следовательно, и режим вынужденных колебаний.

Рис. 8,1. Определение условий существования вынужденных колебаний по годографу / (и).

*) В силу условия (8.1) достаточно изменять ф от О до л, так как изменению ф от п до 2эт будут соответствовать значения ff (п - ф), отличающиеся лишь знаками.

Режим биений и режим захватывания (при соо = const) переходят один в другой при прохождении величиной А некоторых критических значений, которые будем обозначать через Л1кр и Лгкр.

Если Л = Лцр, то кривая (я -ф) при некотором значении Ф = ф1о касается прямой -ко в левой полуплоскости (рис. 8.2,г).

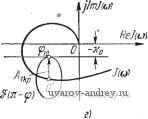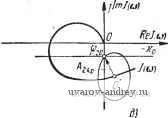Tin-а)

Рис. 8.2. Влияние А на число возможных вынужденных колебаний: А мало (а), Л велико

(б. е). Л=Л,ф (г. а).

Если Л - Лгкр, то кривая - ф) при некотором значении Ф = Ф20 пересекает прямую -хо лишь в точке, где эта прямая пересекает мнимую ось (рис. 8.2,).

Эти значения Л1кр, Лгкр можно найти и в аналитической форме. Непосредственно из рис. 8.2, г имеем

11т5(?с-ф,о) = Im/(a)o) + K (8.6)

Воспользовавшись (8.1), находим

(8.7)

л Г1т/(соо) +Хо1

Го(п-ф,о)

Аналогичным образом из рис. 8.2, й имеем

I (и - ф2о) 1 = 1 /(соо) + / <о I. откуда после подстановки в правую и левую части этого выражения действительных и мнимых частей У (со) и 9{п - фго) получим

2 кр -

К 1 о( -

(соо)]2 + [Im/(coo)p

Ф2о)Г + [Го( -ф20)]

(8.8)

При А > Ащ) искомый сдвиг фаз ф определяется из уравнения, подобного (8.7):

Го(л-ф)==-121/(+,

или, на основании (8.7),

I /о (я - ф) I = f о (я - ф,о).

(8.9) (8.10)

Отсюда следует, что при изменении А сдвиг фаз изменяется по закону, определенному функцией, обратной функции fo-

В табл. 8.1 приведены графики функций fatt) и соответствующие им законы изменения сдвига фаз.

ТАБЛИЦА 8.1 Графики функций f{t) и законы изменения сдвига фаз

Число значений искомого сдвига фаз ф при превышении величиной А критического значения зависит от формы внешнего воздействия l{t) = Afo{f})t - ф). Так, если оно имеет несколько экстремумов внутри полупериода, например, два (рис. 8.3,а), то кривая 5(я -ф) будет иметь вид, показанный на рис. 8.3,6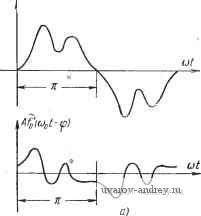

Рис. 8.3. Внешнее периодическое воздействие, его производная (а) и соответствующая

им функция of (л-Ф) (б).

И, следовательно, наибольшее число возможных значений ф не превышает четырех. Формулы (8.4), (8.5) остаются справедливыми и в этих, более сложных, случаях.

Если внешнее воздействие гармоническое, то определение Лкр и ф существенно упрощается. Действительно, предположим, что

ЦтШ f{t) = AfoM - (i>) =

= Л81п(а)/ -ф). (8.11)

Тогда

fo (л - ф) = sin (я - ф), fo (St - ф) = cos (я - ф).

Следовательно, функция 5(я-ф) будет равна

(я - ф) = Л [COS (я - ф) +

+ / sin (я - ф)] = Ае (8.13)

Отсюда заключаем, что 5(я - ф) соответствует окружности радиуса Л. Точки пересечения этой окружности с прямой -ко в левой полуплоскости / определяют возможное значение ф. Фазы Ф можно определять непосредственно из рисунка, не производя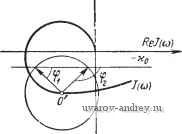

(8.12)

Рис. 8.4. Определение фазы ф при внешнем гармоническом воздействии.

разметки окружности. Для этого нужно из центра окружности (находящегося на кривой / в точке, соответствующей юо (точка О')) провести радиусы А к точкам пересечения ее с прямой -хоь расположенным в левой полуплоскости. Углы ф1 и ф2, образованные этими радиусами с прямой -яоь будут равны искомым значениям (рис. 8.4). Если о (точка О') находится ниже прямой -Хо, то ф1 и ф2 положительны, если же соо (точка О') находится выше прямой -Ко, то ф1 и фа отрицательны.

Критические значения амплитуды внешнего воздействия Л„р определяются весьма просто. Если щ находится в левой полуплоскости, то Лцф определяется длиной перпендикуляра, опущенного из точки О'и соответствующей щ, на прямую -ко

а) 01

Рис. 8.5. Определение Л^р по годографу 1 (со) при положительном (а) н отрицательном

(б) гисгерезисе.

(рис. 8.5, й) или на прямую ко (рис. 8.5,6). Если шо находится в правой полуплоскости, то Лгкр определяется длиной отрезка, проведенного из точки Of, соответствующей юо, в точку пересечения прямой -Ко с мнимой осью.

Таким образом, в данном случае, если

Л<Л, р, (8.14)

то вынужденные колебания частоты соо отсутствуют. При

Л,кр</1<Л2 (8.15)

существуют два периодических решения частоты юо с различными фазами ф1 и фг. Эти фазы связаны соотношением

ф, -Ьф2=±Я. . (8.16)

Л>Л2 (8.17)

(если точка юо лежит в левой полуплоскости) либо при

Л>Л2 р . (8.18)

(если точка юо лежит в правой полуплоскости) существует только одно периодическое решение частоты щ.

При

Критические значения могут быть также определены аналитически по формулам (8.7) и (8.8). В рассматриваемом случае

fo(n -ф) = 81Пф, f о (я - ф) = cos ф. (8.19)

Если точка, соответствующая юо, лежит в левой части плоскости /, то окружность радиуса А = /4,кр касается прямой -хо

слева при ф,(, = -. Следовательно,

Подставляя это значение в (8.7), находим

/1, р = 1т/(соо) + Хо. (8.20)

Если же точка, соответствующая юо, лежит в правой части плоскости /, то окружность радиуса А = Лгкр проходит через точку

пересечения прямой -хо с мнимой осью при ф2о<--- В этом случае

[fo(5t -Ф2о)Р + [Го(5г-Ф2о)Р = соз2ф2о + 8ш2фго=1. (8.21) и, следовательно, по формуле (8.8) находим

Лгкр = l/[Im/(a)) + KoF + [Re/(co)p = /(/со) + /хо . (8.22)

Величина Лг (см. рис. 8.5) определяется также соотношением (8.22). Что же касается сдвига фаз ф1 при Л>Л1кр, то, как следует из рис. 8.4, он определяется выражением

I Im / (ш) -Ь Хо I Л, кр 8тф, 1=-J-= (8.23)

Зная ф1, находим фг из (8.16). Зависимость Л1кр и Лгкр от частоты (О, получаемая непосредственно по годографу /(со) (см. рис. 8.5,(2), изображена качественно на рис. 8.6, с; при хо > О и на рис. 8.6,6 при Хо = 0. Если частота внешнего воздействия равна частоте возможных автоколебаний, то

/1,кр = 0. (8.24)

Следовательно, режим вынужденных колебаний на частоте, близкой к частоте автоколебаний, может иметь место при весьма малой амплитуде внешнего воздействия.

Так как с ростом со (начиная с некоторого значения со) годограф /(со) по модулю уменьшается, то отсюда можно заключить, что при достаточно высоких частотах внешнего периодического воздействия критическое значение амплитуды Лкр становится малым, и, следовательно, может быть выбрана и малая амплитуда внешнего воздействия, чтобы сорвать автоколебания и установить режим вы.нужденных колебаний частоты со. Нижняя граница этой амплитуды равна xq.

Выше мы рассматривали релейные автоматические системы с положительным гистерезисом. Нетрудно видеть, что в этом случае при уменьшении щ критические значения амплитуд для частот, лежащих выше прямой -ко, уменьшаются, а для частот, лежащих ниже прямой -ко, увеличиваются.

При наличии отрицательного гистерезиса прямая -ко заменяется на прямую Ко, проходящую теперь в верхней части плоскости / (см. рис. 8.5,6). В этом случае при уменьшении Хо критические значения амплитуд для точек годографа /(со), лежащих выше прямой Хо, увеличиваются, а для точек /((о), лежащих шже прямой Хо, уменьшаются. При отсутствии гистерезиса в релейном элементе прямая ±ко совпадает с действительной осью. Этот случай имеет свою специфику. Очевидно, что при Хо == О условие отсутствия дополнительных переключений не может выполняться. В этом случае простые периодические режимы сменяются сложными

периодическими режимами. Возможны также движения с остановками и так называемые частично-скользящие режимы (см. главу ХП).

Таким образом, годограф релейной системы /(и) позволяет определить условия существования и найти основные показатели не только автоколебаний, но и вынужденных колебаний.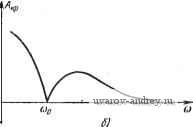

Рис. 8.6. Зависимость А^ от со при >0 (а) и } о=0 б).

§ 8.2. Релейные системы с зоной нечувствительности

При наличии зоны нечувствительности искомыми величинами, определяющими вынужденные колебания, являются фаза ф и относительная длительность у-

Для определения этих величин введем комплекснозначную функцию

{уп - ф) = Afo {уп - ф) -Ь If о (уп - ф), (8.25)

которая при Y= 1 совпадает с 5(я - ф).

Изменение у от О до 1 не влияет на форму кривой, соответствующей (уп - ф), а изменяет лишь оцифровку кривой. При О < Y < 1 значению фо будет соответствовать значение фо + я(1-у)-

Воспользовавшись годографами релейной системы

J, (со) = Re /, (со) + / Im /, (со) = - -4- g- - /2 (-) (8.26)

и

Jy (со) = Re Jy (со) + / Im (со) = - (v -) - /2(v -) (8.26)

составим их суммы с 5(я - ф) и 5(уя - ф), т. е.

5(я-ф)-Ь/1 (со), (уя-ф) + /(со).

(8.27)

Аналогично предыдущему мнимые и действительные части (8.27) при (О = (Оо тождественны левым частям условий надлежащих моментов переключений и направлений переключений (7.8) и (7.8). Поэтому условия существования вынужденных колебаний (7.8) и (7.8) можно представить в форме

I m {S (я - ф) + /, ((Оо)} = - Ко,

Не{5(я-ф) + /;((0о)}<0 -

Im (уя -4>) + Jy (сОо)} = Яко, Не{(ук-ф) + /,(сйо)}<0.

(8.28)

Эти условия можно также интерпретировать геометрически и при заданном значении (о определить ф и у.

Для этой цели воспользуемся семейством годографов /i(co) и Jy{(i)) по параметру у, которое применялось при исследовании автоколебаний.

Проведем на плоскости годографа /i((o) прямую -ко, а иа плоскости годографа /((о) - прямую Яко (рис. 8.7). На каждой кривой годографа отметим точки, соответствующие частоте внешнего воздействия (Оо. На рис. 8.7, а и б эти точки лежат па жирной кривой.

Из точки, соответствующей заданному значению (Оо, на годографе /i(co) при Y = 1 строим как из центра кривую, описываемую концом вектора 5(я - ф). Перемещая эту кривую так, чтобы центр скользил вдоль линии равной частоты, определяем значения ф как отметки на кривой 5(я - ф) в точках пересе-