делить, проводя прямую Рис. 6.41, а. Найденная та-

ким образом зависимость йо от дана на рис. 6.43. С увеличением ко или уменьшением хо относительная частота возможных автоколебаний повышается.

ijlmJiu)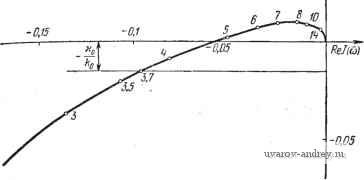

Рис. 6.4;!. Годограф / (col для системы регулирования температуры при йо = 1, Р=0.

oMofiz 0,03 ом oi

Рис. 6.43. Зависнмость бо от4-.

Для увеличения относительной частоты о автоколебаний введем жесткую внутреннюю связь, т. е. ускоряющий элемент с передаточной функцией

Функциональная схема системы с такой внутренней связью изображена на рис. 2.10. Передаточная функция линейной части системы теперь равна

а частотная характеристика

ИЛИ, после введения относительных величин.

где р =-г- , k = K , со = соГа.

Годограф У (со), соответствующий первому слагаемому, был уже ранее построен. Он воспроизведен на рис. 6.44 (кривая /).

Рис, 6,44. Влияние ускоряющего элемента (жесткой внутренней связи) на частоту

возможных автоколебаний.

как сле-

Годограф, соответствующий второму слагаемому

дует из табл. 6.4, равен -{} ~ у) имеет вид, показанный в табл. 6.4. Он изображен на рис. 6.44 (кривая 2) при р = 0,05. Складывая геометрически эти годографы, найдем годограф релейной системы при наличии ускоряющего элемента (кривая 5). Из рассмотрения этой характеристики видно, что частота возможных автоколебаний увеличивается. При р > 0,043 годограф релейной системы не пересекает действительной оси и, как было показано в § 4.8, при ио = О положение равновесия релейной системы в этом случае устойчиво. Если же ио > О, в системе появляются автоколебания, которые не могут быть

2 3 4 5 6 7 8 9 10 12 14

Значения годографа Ii ( )

Re /,

0,026 0,006 0,000 -0,002 -0,002 -0,003 -0,003 -0,002 -0,002 -0,001 -0.001

y=0,5

Re/,

Im/,

y=0,6

Re/,

Im/,

y=0,7

Re/,

Im /,

2 3 4 5 6 7 8 9 10 12 14

-0,053 -0.059 -0,051 -0.041 -0,034 -0,027 -0,022 -0,017 -0.015 -0,009 -0.006

-0,273 -0.115 -0,069 -0.041 -0,024 -0.015 -0,008 -0,005 -0.003 0,001 0.002

Y=0.8

Re/,

Ira /,

-0,172

-0.125 -0,092 -0,071 -0.054 -0.041 -0,032 -0.025 -0.021 -0.011 -0,007

-0.341 -0,143 -0.072 -0,031 -0.020 -0.010 -0,002 0.002 0,003 0,004 0.004

-0,141 -0,103 -0,073 -0,058 -0,045 -0.035 -0,027 -0.020 -0.018 -0.009 0.0ОЭ

0.287 -0,220 -0.061 -0.033 -0.016 -0,008 -0,002 0,000 0,001 0,004 0,003

V=0,9

Re/,

Im /,

Y=I.O

Re /,

Im/,

-0,128

-0.091 -0,065 -0.049 -0,037 -0,032 -0.022 -0.017 -0.015 -0.008 -0.004

-0.226 -0.093 -0.046 -0.024 -0.011 -0,005 -0.001 0.002 0.002 0,004 0.004

Значения годографа Jy( )

Y=0,1

Re/

Y=0,2

Y=0.3

Ira / ,

Y=0,4

Re/ ,

Im 7

2 3 4 5 6 7 8 9 10 12 14

-0,042 -0,014 -0,006 -0,002 0,000 0,001 0,001 0,002 0,002 0,001 0,001

0,046 0,026 0,017 0,013 0,009 0,006 0,005 0,003 0,003 0,001 0,001

-0,095 -0,037 -0,016 -0,008 -0,002 0,000 0,001 0,002 0,002 0,002 0,002

0,074 0,048 0,033 0,024 0,018 0,013 0,010 0,007 0,006 0,003 0,002

-0,156 -0,065 -0,032 -0,017 -0,008 -0,004 0,000 0,001 0,001 0,003 0,002

0,087 0,061 0,044 0,033 -0,025 0,019 0,015 0,011 0,009 0,005 0,003

-0,217 -0,095 -0,050 -0,030 -0,015 -0,003 -0,003 0,000 0,000 +0,003 0,003

0,079 0,064 0,051 0,039 0.031 -0,024 0,019 0,015 0,013 0,007 0,004

Y=0,5

V=0,6

Y=0,7

Re /

Re A,

Im /.,

2 3 4 5 6 7

0,273 0,125 -0,069 -0,041 -0,024 -0,015 -0,008 -0,005 -0,003 0,001 0,002

0,053 0,059 0,051 0,041 0,034 0,027 0,022 0,017 0,015 0,009 0,006

Y=0,8

Re /

Im /..

-0,380 -0,187 -0,110 -0,071 -0,044 -0,029 -0,018 -0,011 -0,009 -0,001 0,000

-0,031 0,031 0,042 0,041 0,036 0,030 0,026 0,022 0,014 0,012 0,008

-0,319 -0,151 -0,092 -0,058 -0,037 -0,025 -0,015 -0,010 -0,008 -0,001 0,000

-0,023 0,028 0,035 0,033 0,030 0,026 0,022 0,018 0,015 0,010 0,007

Y=0,9

Re/.,

Im/.

-0,258 -0,129 -0,076 -0,049 -0,031 -0,021 -0,014 -0,009 -0,007 -0,002 0,000

-0,026 0,015 0,024 0,024 0,023 0,019 0,017 0,014 0,012 0,008 0,006

-0,205 -0,106 -0,066 -0,043 -0,029 -0,020 -0,014 -0,010 -0,007 -0,003 -0,001

-0,064 -0,007 0,009 0,013 0,014 0,012 0,012 0,009 0,009 0,006 0,005

-0,163 -0,092 -0,060 -0,041 -0,029 -0,021 -0,015 -0,011 -0,009 -0.004 -0,002

-0,110 -0,333 -0,009 0,000 0.005 0,006 0.007 0,006 0,006 0,005 0.004

jlmJ,(o)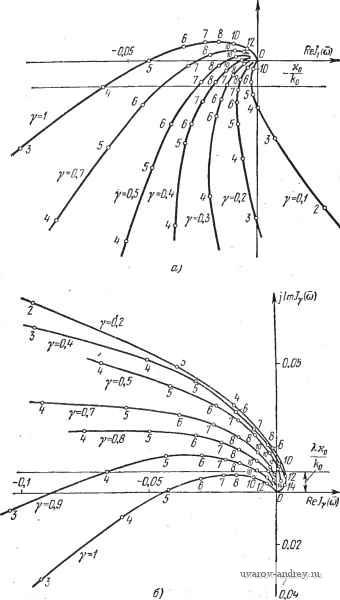

Рис. e.45. Годографы 1\ (и) (о) и /у (и) (б) при = 1 и О < у < 1.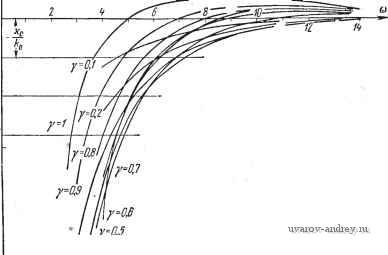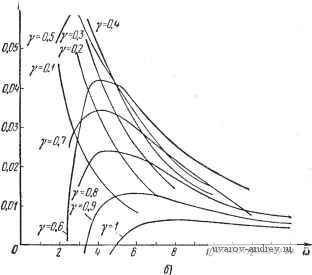

Рис. 6.46. Мнимые части Im 1 (и) (a), Im 1 (и) (б) годографов при = и О < ¥< 1*

К определению и Г^.

устранены никаким изменением линейной части системы. Но чем больше р, тем выше при этом частота возможных автоколебаний.

Рассмотрим теперь эту релейную систему автоматического регулирования температуры при наличии в релейном элементе зоны нечувствительности, полагая, что р = 0.

10 0.8

О

6 8 а)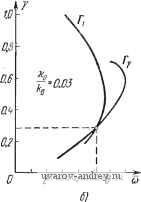

W 0,8 0,Б 0,4 0,2

О

1 I I L-

6 а

Рис. 6.47. Определение параметров автоколебаний и и V при различных по кривым Г]

Пользуясь формулами (6.61) и (6.62), вычисляем годографы релейной системы /i(cu) и /у(й).

Вычисленные значения этих годографов при у, изменяющихся от 0,1 до 1., приведены в табл. 6.5 для /i(c)) и в табл. 6.6 для /у(сй).

Годографы /i(cu) и /у(й), построенные по этим данным, изо-

бражены на рис. 6.45, с и б. Проводя прямые -и

находим, как это было описано ранее, зависимости у = (ю) и у = Гу(ю). Наиболее просто эти зависимости определяются по семейству кривых Im/i(©) и 1т/(ю) (изображенных на рис. 6.46 в диапазоне ю, для которого Re/i(c>) <:0 и Не/у(ю) <0 соответственно), если провести на этих графиках те же прямые, что и ранее. .Полученные таким образом зависимости

у = Г,(ю), у = Г^(ю)

при = 0,015, -g- = 0,03, -g-= 0,045 и А = 1 изображены на

рис. 6.47, а, б, в соответственно.

Точка пересечения кривых у = Г1(ю) и у = Гу(ю) определяет частоту автоколебаний щ и значение у.

Как видно из рис. 6.47, в, наличие достаточной по величине зоны нечувствительности приводит к устранению автоколебаний.

Графики рис. 6.47 показывают, что с ростом ~ частота

О

возможных автоколебаний увеличивается; кроме того, при этом возрастает и у. Начиная с некоторого значения ~ автоколебания устраняются.

Однако, как мы уже говорили, устранение автоколебаний здесь достигается уменьшением точности.

Глава Vn

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В РЕЛЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМАХ

§ 7.1. Понятие о вынужденных колебаниях

Предположим, что к релейной автоматической системе приложено внешнее периодическое воздействие t{t), такое, что

f(+t)=-f<>-

(7.1)

где--полупериод.

Внешнее воздействие может быть приложено к любой точке релейной системы и, в частности, ко входу релейного элемента.

Далее будем предполагать, что внешнее воздействие приложено ко входу релейного элемента, как это показано на рис. 7.1. Это предположение не является ограничительным, так

ис. 7.1. Релейная автоматическая система при наличии внешнего периодического

воздействия.

как, пользуясь приемами, описанными в §§ 2.1 и 2.5, можно всегда привести внешнее воздействие ко входу релейного элемента.

При наличии внешнего периодического воздействия в релейной системе возможны три режима.. Первый режим соответствует биению между автоколебаниями и вынужденными колебаниями, вызываемыми внешним периодическим воздействием. Этот режим в некотором смысле подобен режиму биений между собственными колебаниями и вынужденными колебаниями в линейных системах.

Второй режим, являющийся характерной особенностью нелинейных и, в частности, релейных систем, состоит в том, что внешнее периодическое воздействие навязывает системе свою частоту и подавляет автоколебания, возможные в системе.

в этом случае система автоматически синхронизируется частотой внешнего воздействия. В ней имеют место вынужденные колебания, частота которых равна частоте внешнего воздействия.

Это явление, наблюдавшееся еще Гюйгенсом на механических системах - двух часах, висевших на одной и той же стене, довольно подробно изучалось и использовалось в радиотехнике. Сейчас оно находит применение и в технике автоматического управления.

Режим, связанный с подавлением автоколебаний, часто называют принудительной синхронизацией или, наконец, захватыванием на основной частоте. В дальнейшем будем называть его реоюимом захватывания или режимом основных вынужденных колебаний, в отличие от режима биений, которому соответствует наличие автоколебаний наряду с вынужденными колебаниями.

Третий режим также подавляет автоколебания, но при этом навязывает системе вынужденные колебания, частота которых

г

не совпадает с частотой внешнего воздействия, а составляет -

часть от этой частоты, где v- целое положительное число. Такой режим, связанный также с подавлением автоколебаний, иногда называют принудительной синхронизацией на субгаю-мониках или захватыванием на частоте субгармоник. Будем называть такой режим по традиции субгармоническим, хотя и здесь речь идет не о гармонических колебаниях, а о сложных периодических колебаниях частоты, в v раз меньшей частоты внешнего воздействия. Режимы захватывания на основной частоте или частоте субгармоник являются периодическими режимами, тогда как режим биений, вообще говоря, является непериодическим режимом.

Все эти режимы определяются решениями уравнения релейной системы

Г {Z (t)} = W{p)L [Ф if (t) - г (ty, а)}, (7.2)

где f{t) - внешнее периодическое воздействие частоты а.

Если существует периодическое решение уравнения (7.2), изменяющееся с частотой шо = а>в, то это значит, что в релейной системе может иметь место режим вынужденных колебаний основной частоты и что при этом внешнее периодическое воздействие частоты шо подавляет возможные автоколебания в релейной автоматической системе.

Если существует периодическое решение уравнения (7.2),

СОв

изменяющееся с частотой 0 = -то это значит, что в релейной автоматической системе может иметь место режим вынуж-