системы. Так как рассматриваемая САУ с ЧИМ является нелинейной, то в ней возможны различные типы устойчивых автоколебательных процессов. Определение устойчивости № общем виде достаточно сложно. Правильно спроектированная система должна удовлетворять условиям устойчивости в малом с достаточным запасом.

Найдем рекуррентное соотношение, связывающее значения фазовых координат в моменты поступления двух соседних им пульсов/вьш, причем между этими двумя импульсами поступает один импульс /в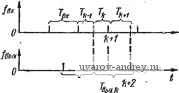

Рис. 40. К расчету устойчивости САУ

(рис. 40), как это происходит в установившемся режиме. Если в соотношении (61) заменить Т^у. - на Tk+\, то получим:

I Xk+2 = F {Tk+i) [F (П) X, + b (Г,) Хвх + с (Г,) +

+ b (П+i) д^вх + с (Tk+i) (Mft + d). (72)

Из рис. 40

Tk-i +П = Гвх-, Tk + Tk+x = Tyj,. (72а)

I Значения Ти-\ и Tk+\ связаны рекуррентным соотношением

Tft+l = Т'вых/г - Т^вх + Tft-1- (73)

Учитывая свойства матрицы F векторов bncF (Tj) F (Га) = = F (Г, + Т,); F (Г,) b (Г,)+Ь (Т,) = fc (Г^ + 7); F (Т,) X X с (Г^) -f с (Г2) = с (Ti -\- Tg) и подставляя соотношение (73) в выражение (72), получаем

I. Xk+2 = F (Гвыхб) Xk + b (Гвыхй) ЛГвх + С (Т^ыхк) Щ + + с (Гвыхй - Т^вх + Tft-i) d, (74)

де Т^выхА = ф (Xk, Tk-\) и определяется видом модуляции. Уравнения (73) и (74) образуют искомые рекуррентные соотношения порядка м -f Ь

Введем квадратную матрицу R порядка + 1. элементы которой rq являются частными производными t-й строки системы (73), (74) по % при / = I, п или по Tk-i при / =, = п + 1, причем П1 вычисляются в точке равновесия. Для устойчивой системы все собственные числа R по модулю меньше 1.

Пример 3. Пусть на рис. 37, б Wa = k, W p=fe (Гр-.1)-1 Воспользовавшись соотношениями (64) и (74), запишем

+ kXd (1 - е-вых*-вх+Гд-,)/7-з^

Продифференцируем правую часть этого равенства по х^, положив вых ~ *Р 7ft i). После подстановки в этот результат координаты точки равновесия Xk = л^ых выхй ~ вх- получим

-у- е (*вых з^вх 31 о)

Tk-1

J. - - (76)

Подставляя в выражение (76) = 7 - 7, а также e* из

соотношения (66), получаем

1 = 6--+ (d + + о - W*3) . (77)

Аналогично определяем

ги = [(1 + дТ/дТ 1) (Vsx + d + о - *1 W*3) -

- Г^ (*,л;ех + о - >*вых/*з)]/7з; (78)

a=57bb,xft/5ft-. =2=l+5rBb,xft/57ft l. (79)

Условия устойчивости запишем в виде [36]

1 11~*22~1~ 11 22 1221 О

is21 > 0; (80)

1 - llS2 + l2-21 > 0.

Ограничивающим является второе неравенство. Подставим в выражение (70) значение х^ 1 из выражения (64а), а также исключим Г^, и Tk с помощью соотношения (72а). Получим следующее неявное урав-ление, связывающее Т^, с Xk ч Т^ 1:

= АрЧ XkT (1 - g-ft/s) + (д, + k]-\) (Tk - Т'з +

- Гз + Гзе--,хй+=-=-1/з). (81)

Производные dTJdXk, дТдТ 1 находятся по правилам дифференцирования неявных функций:

I 5Гз, /Зл:б = >г^ ; ar3 x/57fc-l=-7-ft ,/7-Bb,x- (2)

Выполняя дифференцирование и подставляя координаты исследуемой точки из формул (66) и (71), получаем

т-вых^вых; ;=Гз(1-Г -:

-г /г (3)

ll7- , = - (1 - е ) №,- :вх + О - Мвых/з).

Подставляя выражения (82) и (83) в соотношения (77) - (79), а 1атем коэффициенты во второе неравенство (80), получаем условие остойчивости в виде

Приведенный выше анализ относится к цифровому интегратору с реверсивным счетчиком с ПКН на его выходе. При использовании цифрового интегратора с ШИМ анализ усложняется, однако следует иметь в виду следующее. Частота колебаний выходного триггера /тр выбирается значительно большей, чем частота среза системы, поэтому если /вых ~ /тр . то эффект квантования по времени можно не учитывать. Если же /вых < /тр. то учет квантования по времени можно произвести по приведенным выше формулам.

Особенностью САУ с цифровым интегратором с ШИЛ\ является наличие автоколебаний, вызванных квантованием по уровню. Структурная схема для расчета автоколебаний

показана на рис. 41, а, нелинейные характеристики звена НП - на рис. 41, б, е.

Передаточная функция линейной части

НП 4. РСр)

Ф(р) = 0,5о.р(р)(1 +

(85)

1,5 v[t]

где при отсутствии аналогового регулятора ~ 0. Эффектом квантования по времени при расчете режима автоколебаний пренебрегаем.

Для нахождения периода и амплитуды автоколебаний применим метод, описанный в работе [42]. В режиме установившихся колебаний у (t) имеет вид прямоугольных колебаний с амплитудой / и полупериодом 6. Если

Рис. 41. Структурная схема для расчета автоколебаний в САУ с цифровым интегратором (а), нелинейные характеристики (б, е)

Ф (р)1р = Ф (0)/р -f dk/iP + Pk), fc=l

(86)

то и (t) на отрезке [О, 6] в квазиустановившемся режиме (после затухания составляюших, вызванных начальными условиями) будет изменяться по закону

uit)Ф (0) (/ - 6/2) + 1 4 {1 [1 + th (р,е/2)] e-iypk.

Для определения 6 служит уравнение периодов

W (G) = Ф (0)

= 0,5,

фичем устойчивые колебания возможны только для таких

>о.

корней 0 уравнения (88), для которых -

Условия переключения имеют вид -р-

7ри правильном выборе параметров системы 6 Гтр. Следовательно, учесть квантование по времени, вносимое (ифровым интегратором, можно введением запаздывания г момента, когда и {t) станет равным 0,5, до момента пе-еключения. Это запаздывание не превосходит Гтр. При том уравнение (88) запишем в виде

(0 Гхр) = О,5, (89)

условия переключения

du(t)

>0.

Пример 4. Пусть lFp = fe/Tp+l, Wa(p) = О, тогда Ф (р) =

= 0,5kkidATp + 1) = k,/(Tp+ 1) и Ф {р}/р = fe, lp- -{р+ Т-)-]. Согласно формуле (88) (6/2 - ГШ е/2Г) = 0,5, или О.Б^Г = v = = г - th z (г = 6/(27)). Решение этого уравнения дано в табл. 3.

L Таблица 3

Зная В, подставляем это значение в соотношение (87), вычисляем значения и (/) при / =0и/ = Ои проверяем, не выходят ли колебания и {{) за пределы одного кванта . Если это явление происходит, то пользуемся более сложной нелинейной характеристикой рис. (41, е).

. Пусть Г = 1 с; fea = Ю; v = = 0,05. По табл. 3 г = 0,55, отку-

G= 1,1 с. Учтем теперь запаздывание Т^. Обозначив Т^/Т = (3

из соотношений (87) и (89), получим уравнение

Если Р = 0.05, то 2 = 0,65, 6=-1,3, а (6) 10 [0,65 - I + (1 + -Ь th 0,65) е~] = 0,78, т.е. меньше, чем 1,5, когда происходит пере-ход на следуюший участок нелинейности.

Кроме этого можно применить метод, предложенный в работе [42]. Для систем высокого порядка можно найти частоту автоколебаний графически без определения корней характеристического уравнения.

Глава пятая

ПРИМЕРЫ ВЫПОЛНЕНИЯ И РАСЧЕТА ЦИФРОАНАЛОГОВЫХ САУ

1. ЦИФРОАНАЛОГОВАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ

Электродвигатели некоторых производственных механизмов должны поддерживать и регулировать частоту вращения с точностью 0,1 % и выще. Особенно высокие требования к точности поддержания частоты вращения предъявляются в тех случаях, когда обрабатываемый материал находится одновременно в нескольких механизмах (непрерывные прокатные станы, бумагоделательные машины) и когда возникновение небольшого рассогласования может привести к порче материала. Такая точность не может быть обеспечена только аналоговыми системами регулирования, поэтому применяются цифроаналоговые системы (рис. 42).

Электродвигатель постоянного тока М получает питание от регулируемого источника напряжения-тиристорного преобразователя ТП. Частота вращения задается в виде частотного сигнала, частота импульсов которого пропорциональна заданной частоте со. В качестве датчика об-

ратной связи используется тахогенератор BP переменного тока ТТ-245. Напряжения каждой из его двух трехфазных обмоток выпрямляются с помощью мостовой схемы; затем выходные напряжения суммируются, так что напряжение 0.с имеет 12-фазные пульсации небольшой амплитуды, которые легко отфильтровываются фильтром с постоянной

ПЧН

ДТ{М)-\:\-

т

Рис. 42. Схема САУ частоты вращения электродвигателя с цифровым корректором

времени 5... 10 мс.

Аналоговая часть системы регулирования строится по принципу подчиненного регулирования параметров 134]. В контуре регулирования якорного тока двигателя находится операционный усилитель, имеющий передаточную функцию интегро-пропорционального звена = (Tgp + + \)/TjP, причем принимается равной электромагнитной постоянной времени якорной цепи двигателя (с учетом внутреннего сопротивления преобразователя). На входе этого усилителя сравниваются выходной сигнал усилителя. Выполняющего роль регулятора частоты вращения, и сигнал, пропорциональный току якоря.

при расчете контура частоты вращения предполагается, что в нем содержится некомпенсируемая постоянная времени Гц, равная сумме постоянной времени фильтра на выходе тахогенератора и эквивалентной инерционности замкнутого контура регулирования тока l/co, где - частота среза контура тока. Операционный усилитель регулятора скорости работает в режиме пропорционального звена, причем его коэффициент усиления /го.у выбирается таким, что частота среза контура скорости = 1/(27,

где Сй(, о-У ос-ком (Оиом/(Г„ X Ид.т.пом); о.сном - НаП-

ряжение на выходе аналогового датчика обратной связи по скорости при номинальной скорости вращения; (АОиом - относительное падение скорости вращения двигателя при изменении нагрузки от нуля до номинальной величины при отсутствии цифрового корректора, Ид.т.ном - напряжение на выходе датчика обратной связи по току ДТ при номинальном токе якоря; - электромеханическая постоянная времени двигателя с приводимым им механизмом. При этом реакция аналоговой части системы на толчок задания имеет перерегулирование 4,3%.

При появлении статического момента на валу двигателя возникает ошибка по скорости Асо, причем отношение величины этой ошибки к величине изменения скорости вращения без регулятора Асо': Асо/Асо' = 1/(а)(.Г„). Для ликвидации ошибки Асо, а также погрешностей аналоговых задающих устройств и датчиков обратных связей применя-егся цифровой корректор частоты вращения, основную часть которого образует цифровой интегратор разности частот ЦИ. В качестве на него поступает задающая частота /эт, а в качестве /2 - частота обратной связи /вых- Эта частота формируется из фазных напряжений тахогенератора. Число импульсов на оборот датчика равно 552, а максимальная частота /вых - 9,2 кГц (для ш = 105Vc). С помощью индикатора скорости ИС можно визуально наблюдать за точным значением частоты вращения. Выходной сигнал ЦИ поступает на вход усилителя регулятора

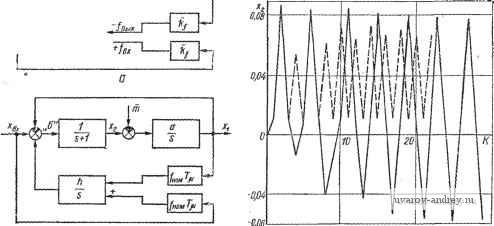6 Ъ

Рис. 43. САУ частоты вращения с цифровым корректором:

а - структурная схема для абсолютных параметров; б - структурная схема для относительных параметров; в - переходные процессы

скорости, складываясь алгебраически с напряжением задания 3. Поскольку напряжение ы„ будет изменяться до тех пор, пока не будег достигнуто равенство == /вых, то частота вращения двигателя будет точно равна заданной.

Рассмотрим основные соотнощения в цифроаналогоюй системе регулирования частоты вращения. Пусть система предельная непрерывная. Явлениями квантования во времени и по уровню пренебрегаем.

Структурная схема системы регулирования САУ частоты с цифровым корректором показана на рис. 43, а. Выходной величиной является ЭДС двигателя, а kf = hb/Esbn = /вх/вх; /стРя - падение напряжения в якорной цепи под действием статического тока (тока нагрузки) / ; / = dkkE ou/Uo.c.mu, h - отношение коэффициента усиления регулятора скорости по каналу ЦИ к коэффициенту усиления по каналу основной (аналоговой) обратной связи. Для получения более общих результатов введем относительные переменные a;i= £вых/£ном; =lRJ{TE,y)\ т = IctRJ (Т„а)Е„ом); h = £ ом, а также относительное время X = Из теории преобразования Лапласа известно, что при такой замене передаточная функция системы имеет прежний вид, но оператор р должен быть заменен на оператор s = рГ,.

Структурная схема рис. 43, а сводится к схеме рис. 43, б. Реальные частоты заменяются на относительные, имеющие периоды Ybx == Гвх/Гц; 7вых = Т^ъ^/Тц; а = ГцЮ^. Закон ЧИМ в абсолютных и относительных переменных записывается соответственно в виде

вых Увых

J £вых(0<= l/f. J ЛГЛО - 1/(/номТ)- (90)

и о

Если разомкнуть систему в точке б, то получим передаточную функцию разомкнутой системы в виде

W = a{l+ns)lns{s+l), (91)