тричных относительно плоскости ху точкам той же поверхности с отрицательными абсциссами.

3. Поверхность z - f (х, \у\) состоит из точек поверхности Z = f {х, у) с положительными ординатами и точек, симметричных относительно zx точкам той же поверхности с отрицательными ординатами.

При использовании положений 1, 2, 3 следует иметь в виду, что модулирование четных степеней переменных не приводит к преобразованиям поверхностей. Однако можно прибегать к модулированию слагаемых и множителей при этих переменных.

Пример 5. Пусть дано уравнение сферы, л: X -\- - fi. Преобразуем его к виду (xf + (2г/)2 -\- (22) = 4fi v. после этого осуществим операцию модулирования:

(ДГ + л:)2-4-({/4-j/)2 + (2 + 2)2 = 4/-2. -(28)

При л; О уравнению (28) соответствует полусфера + у^ -\- = fi, при x<Q - поверхность проецирующего цилиндра у^ X = fi. Таким образом, уравнению (28) соответствует обвод, составленный из указанных выше поверхностей.

Пример 6. Переведем уравнение (2xf -f (2yf + (22) = 4fi в уравнение (x+\x\f+(y + \y\f + Az = Afi. (29)

При X 0, {/ О уравнению соответствует четверть сферы х^ -\- у' -\- г' - = fi, заключенная между координатными плоскостями гх и zy; при О, {/ << О полуцилиндр х^ + 2 = fi, расположенной по одну сторону от плоскости zx; при О, х<0 уравнению соответствует полуцилиндр z = fi, распо-

ложенный по одну сторону от плоскости zy; при х^О, у<0 пара отсеков пло-. скостей г= 1 и г= -1, расположенных в квадранте плоскостей -гу и -гх.

Таким образом, уравнению (29) соответствует обвод пяти отсеков поверхнТ)-стей, указанных выше.

Пример 7. Уравнению

{x+\x\f-{y+\y\r = 8z (30)

при л;0, у^О соответствует .четвертая часть гиперболического параболоида х^ - у^ - 2г, заключенная в квадранте координатных плоскостей zx и гу; при х^О, у<0 - половина параболического цилиндра х^ = 2г, расположенная над плоскостью ху по одну сторону от координатной плоскости ху; при д; < О, у^ О - половина параболического цилиндра -у^ = 2г, расположенная под плоскостью ху по одну сторону от плоскости гх; при х <0, у <:0 - отсек плоскости 2=0, заключенный в квадрант плоскостей гх и гу. Таким образом, уравнению (30) соответствует обвод четырех отсеков указанных поверхностей.

Другой способ составления уравнений областей, получаемых непрерывным перемещением трехмерных фигур, основан на следующих положениях.

Пусть F (х, у, Z, /) есть уравнение какой-нибудь фигуры трехмерного пространства, С = (f (х,-у, z, t) есть параметр фигуры Ф, выраженный в явном виде, С^ах и Сп, - максимальное и минимальное значения параметра С, принимаемые этим параметром при непрерывном перемещении фигуры Ф. Тогда

фигура, получаемая при непрерывном перемещении в пространстве фигуры Ф, описывается уравнением

I ф (X, у, Z,. . ., О - С^ах 1 + I ф (Х, У, Z, t) - С„, I = С„ах

(31)

Справедливость этого положения вытекает из рассмотрения уравнения отрезка числовой оси, точки которой снабжены весами.

Пример 8. Пусть задана поверхность сферы -\- -\- = 25 с цилиндрическим отверстием, ограниченным цилиндром. Введем в рассмотрение кольцо с внешней границей в виде окружности Ух -\-У^= V2&~z и с внутренней границей в виде окружности Yx -\- = 2. При параллельном переносе этого кольца с переменной внешней границей получается внутренняя часть нашей сложной поверхности. Уравнение области, ограниченной этой поверхностью, имеет вид

\Ух-\-у^ )/25-г2 \ + \VJF+ -2\=V25-z -2.

Отметим еще одно положение, на основании которого можно составлять уравнения областей, ограниченных сложными поверхностями. Если в пространстве задана область Ф, уравнение которой записано по правилу (31), то уравнение общей области фигуры Ф и некоторой трехмерной фигуры, описанной уравнением 6 (х, у, Z, t) = О, записывается следующим образом:

ф + 6-Сп,ах + ф-С„1п|-Сшах + С„т = 0.

Пример 9. Уравнение отсека цилиндрической поверхности -\-(у - 5) -

- 25 = О, расположенного внутри сферы х^{/ + - 100 = О, имеет следующий вид:

\Vx+y + z +x + (y-5) - 35\ + \Vx + y + z 1-10 = 0.

Пример 10. Уравнение отсека сферы х^ + у^ z - 100 = О, ограниченного плоскостями х-\-у-{-г=0, iix-}-y-\-z - 10= О, записывается следующим образом:

- \x + y + z + x + y + z- 1104->;4-j/4-z-10 = 0.

Основаниями для алгоритмической записи сложных пространственных фигур могут являться следующие положения.

Введем в рассмотрение функцию двух переменных S IF (х, у)], которую определим следующим образом: f (х, у) > О - 5 [F (х, у)1 = -fl; F (х, у) < О - S [F (х, у)\ не определена в действительной области.

При записи уравнения поверхности z = f (х, у) в виде z = = S IF (х, у) I f (X, у) точки поверхности F (х, у) <0 не рассматриваются (удаляются с поверхности). В частности, уравнению

z = S ly-F{x)]f{x, у)

соответствует та часть поверхности z - f (х, у), для точек которой у F (х).

Уравнению

S [(y-Fxix)){y-F,ix))]iz~0)

соответствует та часть плоскости z = О, для точек которой ни у - Fi {х), ни у - F{x) не являются отрицательными величинами.

Пример П. На полусфере г= V-х^-у^ + при записи ее в виде г = = S [у - sin х] ]f -х^-у' + к рассмотрению остается только та ее часть, для точек которой у sin х.

Пример 12. Уравнению z = S [х^ -\-у^ ~ fi] ]f - х^ - {/* + соответствует та часть сферы, точки которой не проецируются внутрь окружности х^ + 1/2=/.

Пример 13. Пусть требуется записать уравнение области на плоскости ху, внешней границей которой является окружность Х^ + у^ = 16, имеющая четыре отверстия, границьг которых есть окружности

X--f (J/- 2) = Ц (;с - 2)2 4-{/2 = 1;

-Ь (г/-h 2)2 = 1; (л:-Ь 2)2 + {/2 = 1. ,

Искомое уравнение запишется так:

Si Ы + (У- 2}2 - 1] S2 [{X 2)2 + {/2 1] 5з [2 1] X

X[(a: + 2)2 + j/2 l]Sg [16 ;c2-j/2](2-0)=0. (32)

Пример 14. Уравнение области прямоугольника, ограниченного прямыми у = 2, у = Ъ, х~ 3, X - А, запишется так:

Si[y - 2]S[Z~y\Ss[x~2,\S[4-x]{z~(i) = (i. .

Пример 15. Допустим, что окружность с четырьмя отверстиями, рассмотренная в примере 13, заметает область от плоскости z = 2 до плоскости г = Б. Уравнение полученного при этом цилиндрического отсека с четырьмя цилиндрическими отверстиями, запишется следующим образом:

SSSsSSS [(г 2) (Б - Z)] (Z - Л) = О,

где Si, Sa, Sg, S4, Sg функции, взятые из-уравнения (32); h - переменный параметр.

Глава III. АВТОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ ПОВЕРХНОСТЕЙ И РЕШЕНИЕ ЗАДАЧ НА НИХ

1, АВТОМАТИЧЕСКОЕ ПОСТРОЕНИЕ

ИЗОБРАЖЕНИЯ КРИВОЙ ПОВЕРХНОСТИ

При автоматическом построении изображений поверхностей возникают специфические проблемы создания формальных моделей и алгоритмов для ЭЦВМ процессов вычерчивания множества линий, задающего поверхность на обратимом чертеже. В это множество в общем случае обычно входит каркас поверхности и очерк. Рассмотрим методы и формальные модели решения задач автоматического вычерчивания линий каркаса, заданных различным образом, а также линий очерка.

Автоматическое построение линии уровня. Пусть имеется функция F (х, у, z), в неявной форме выражающая некоторую поверхность. Тогда при задании одной из переменных, например z = = R, получим уравнение линии уровня этой поверхности. С помощью множества линий уровня можно получить изображение каркаса поверхности. Для того чтобы автоматизировать вычерчивание каркаса, необходимо уметь автоматически вычерчивать линии уровня. Рассмотрим эту задачу.

Пусть задано уравнение односвязной кривой линии в неявной форме: f (х, у) - R = 0. Требуется автоматически вычертить данную линию. При этом необходимо использовать стандартные ЭВМ, которые работают на дискретном цифровом принципе. Использо- вание такой техники приводит к решению следующих задач.

1. Преобразовать кривую, заданную уравнением, из непрерывной формы в дискретную.

2. Определить в дискретном образе те точки, которые на кривой являются смежными и подлежат соединению.

3. Определить последовательность соединения пар смежных точек и тип линии соединения.

Допустим, что форма кривой известна. При этом задана область существования функции: а х Ь; с < у < d.

Для работы графопостроителя необходимо непрерывную кривую представить в виде ряда точек. Введем прямые, параллельные

одной из осей координат (например, оси Оу) так, чтобы: х = а; й -f Д; а -f 2Д, Ь. Будем решать совместно исходное уравнение кривой и уравнение введенной прямой. В результате решения получим координаты точек кривой. Геометрически корни системы определяют точки пересечения вводимых прямых с заданной кривой. Подобным образом можно ввести прямые, параллельные оси Ох. Таким образом, поставленная задача решается наложением на область существования функции достаточно частой координатной сетки. Такой прием встречается в работах многих отечественных и зарубежных авторов. Однако здесь возникает проблема выбора шага такой координатной сетки. Задание слишком частой сетки требует большой машинной памяти и времени. Слишком редкая сетка может привести к потере информации об особенностях формы вычерчиваемой кривой и искажению ее изображения.

Рассмотрим алгоритм, в котором частота координатной сетки может автоматически изменяться в зависимости от особенностей кривой.

Описание алгоритма вычерчивания кривой с автоматическим выбором частоты координатной сетки в зависимости от особенностей кривой линии. Предлагаемый читателю алгоритм обеспечивает изменение величины шага А координатной сетки в случае возникновения признаков, сигнализирующих о появлении таких особенностей кривой, которые могут быть пропущены, если проходить поле с исходным постоянным шагом. Дано уравнение кривой линии

f {х, у) - R = 0; й < ж < fc; с < г/ < d.

Введем координатную сетку из прямых, параллельных оси Оу с некоторым шагом Д, величина которого назначается в зависимости от размеров области существования функции. Весь алгоритмический процесс выявления точек, принадлежащих данной кривой, и варьирование частоты координатной сетки в зависимости от выявляющихся особенностей линии, можно проследить на рис. 13. Из рисунка видно, что на границе области существования функции при X = а нет корней, т. е. прямая л; = й не пересекается с данной кривой (k = 0).

Введем вторую прямую сетки л; = а -f Д. Решение системы дает два корня, т. е. прямая пересекается с кривой в двух точках {kx = 2). Введем ситуацию возмущение . Как только возникает положение, что число корней на последующем шаге не равно числу, корней на предыдущем шаге, то возникает ситуация возмущения. Так как мы имеем дело с односвязной кривой, то ситуация возмущения означает, что между прямыми х = а и л; = й-1-Д ( подозрительная область) находится прямая, которая может быть касательной к данной кривой, т. е. пересечется с ней в двух бес-конечн9 близких точках. Иными словами, между рассматриваемыми прямыми имеется какая-то особенность кривой.

S. k\=0

-(Возмущение)

ki 2

(возмущение)

(Возмущение)

2 3Xi

<3---

Зона 1

Зона и

13 <3

Рис, 13, Алгоритмическое вычерчивание кривой

Для исследования области между этими прямыми применяется несколько модифицированный метод Кифера, Модификация заключается в выборе следующего промежутка, где сохраняется первоначальная ситуация (неравенство числа корней на смежных прямых координатной сети), Подозрительная область сначала делится пополам прямой х = а -\- 0,5Д, Эта прямая, как показывает решение системы, не пересекается с Данной кривой линией {k = 0), но она сузила область исследования вдвое. Теперь область между прямыми л: = а + 0,5Д и л; = с + Д является подозрительной на существование особенностей кривой. Разделим ее пополам прямой х = а -\- 0,75Д, Допустим, решение системы даст два корня, расположенных, очень близко и отличающихся на величину е, где е - принятая точность решения. Прямую X ~ а -\- 0,75Д можно принять за касательную в данной точке кривой. Назовем такую прямую границей зоны , а точки, общие для такой прямой и кривой, - двойными .

В памяти машины образуются два' массива: массив а -[- Д и массив а -\- 0,75Д, в которых точки располагаются по возрастанию ординаты. Двойная точка на прямой а -{- 0,75Д записывается дважды, в массив корней и в массив двойных точек. Это необходимо для того, чтобы выделить эти точки среди других, так как они играют несколько особую роль в работе алгоритма последо- . вательного соединения точек кривой. На рис. 13 сделан следующий

Рис. и. Алгоритмическое соединение смежных точек кривой

шаг: X = а -{- 2Д, и так как число корней на этом шаге равно числу корней на предыдущем шаге, то можно продолжать процесс.

Делается следующий шаг, на котором 4 Ф kg. Значит, можно предположить, что в пройденной области имеется какая-то особенность кривой. Тогда область исследуется более подробно методом, описанным для интервала й + Д. Таким образом, будут найдены имеются двойные точки. Эти точки Для выявления особенностей, кото-

границы зон, на которых также запишутся дважды, рые могут находиться между прямыми (например, л; = а -f Д и X = а -\- 2Д), предусматривается аналогичный пошаговый проход прямыми, параллельными оси Ох.

Описание алгоритма вычерчивания кривой. Для определения точек кривой, которые при вычерчивании являются смежными, используется принцип конкурирования точек, известный в начертательной геометрии и применяемый обычно при определении видимости. В качестве исходных данных для работы данного алгоритма имеем массивы точек, расположенных на линиях координатной сетки, т. е. имеющих, например, одинаковую абсциссу и расположенных по возрастанию ординаты. Имеются также метки точек, которые будут записываться дважды (двойные точки), и метки границ зон, проходящих через эти точки.

Выходом алгоритма являются массивы для вычерчивания.

Геометрическая модель формирования массивов вычерчивания реализуется в машине просмотром массивов точек, построенных на одной ординате.

Рассмотрим отдельные шаги алгоритма. Обратимся к рис. 14. Выберем некоторое направление S, параллельное Оу. Если посмотреть по прямой X = а -\- 0,75Д в направлении S, то видим точку которая имеет метку двойной точки. Эта точка записывается первой в массив вычерчивания, но так как она двойная, то из массива корней не вычеркивается. Смотрим в направлении S по следующей прямой, на которой имеются точки. Видимой оказывается точка 2. Она записывается второй в массив вычерчивания , а из массива корней вычеркивается (так как она не двойная). Затем просматривается прямая й + видимой на ней оказывается точка 3, которая также записывается в массив вычерчивания, а из массива корней вычеркивается, и т. д. до точки 7.

Следующей прямой идет вторая граница рассматриваемой зоны. Если посмотреть по ней в направлении S, то видимой оказывается точка, имеющая метку двойная. В алгоритм заложено правило, что двойная точка пишется как две точки в массив вычерчивания той зоны из двух смежных, в которой на прямой имеется больше точек. В данном случае, когда на прямой оказывается видимой двойная точка, алгоритм проверяет, К какой зоне эту точку отнести. Так как в зоне / на прямых имеются по две точки, а в зоне - по четыре (см. рис. 13), то эта двойная точка в массив вычерчивания зоны / не войдет. Она пропускается и берется следую--щая точка по видимости (точка 8), которая соединяется с точкой 7. Все недвойные точки на границе зоны (например, точка 8) обладают тем свойством, что они записываются в двух смежных массивах вычерчивания, поэтому при записи первый раз в массив вычерчивания точка 8 из массива корней не вычеркивается.

Переходим опять к первой границе зоны /. На ней имеется одна двойная точка /, которая была уже записана в массив вычерчивания один раз. Таким образом, для первой зоны будет формироваться второй массив вычерчивания.Первой точкой в него войдет точка /. Если посмотреть в направлении S по следующей прямой, то так как точка 2 уже вычеркнута, в массиве корней будет видима точка 9, которая войдет в массив вычерчивания, и т. д. до точки 13. Эта точка находится на границе зоны и по приведенным выше правилам алгоритма после записи в массив вычерчивания из массива корней не вычеркивается. После проверки, есть ли еще точки в массивах корней зоны /, можно переходить к зоне .

Если- посмотреть в направлении S по первой границе зоны , то мы увидим точку J. Алгоритм определяет, что эта двойная точка и что она относится к зоне (так как она лежит на границе зон / и , но в зоне на одной прямой больше точек, чем на одной прямой Б зоне. /). Точку / записывают в первый массив вычер- 1ивания, а так как она двойная и ее записали.в первый раз, то из массива корней не вычеркивается. По второй прямой видима точка 2. Она записывается в массив вычерчивания, а из массива корней вычеркивается. Таким образом, будет создано четыре массива вычерчивания во второй зоне: 2, 5, 4, 5; /, 6, 7, 9; 8, 10, 11, 12, 9; 13, 14, 15, 16. Аналогично будут сформированы два массива вычерчивания для третьей зоны: 5, 1, 2, 3, 4, 5, 6, 7; 13; 8, 9, 10, и, 12, 14, 7. Выходом алгоритма являются несколько массивов вычерчивания по зонам, которые и будут служить ис-ходными^данными для работы графопостроителя.

Возможности алгоритма. Алгоритм работает на жордановых кривых и некоторых многосвязных (рис. 15). Однако имеется картотека многосвязных кривых, на которых алгоритм не будет работоспособным, т. е. не полностью выявит характер кривой, хотя это возможно при использовании координатной сетки с прямыми, параллельными оси Ох. Алгоритм позволяет выявлять особенности кривой, заданной в неявной форме. В качестве исходной

(Г

л. о

Рис. 15. Примеры миогосвязных кривых

может быть задана кривая и в графической форме. Например, задан каркас поверхности в горизонталях в виде плана и требуется получить изображение этой поверхности в аксонометрии. В таких случаях на чертеже наносится координатная сетка, выявляющая только двойные либо особые точки кривых. После этого наносится сетка со стандартным шагом, дающая промежуточные точки кривой. В этом заключается ручное кодирование чертежа, по которому ведется работа. Исходными данными здесь, являются массивы ординат, имеющих одинаковую абсциссу. Эти массивы аналогичны тем, которые получаются при вычислении корней, когда кривая задана в неявной форме. В рассматриваемом случае массивы составляются с учетом возможности зрительно оценить особенности кривой. Работа алгоритма возможна и при автоматическом считывании чертежа.

Изложенный алгоритм обеспечивает автоматическое вычерчивание линий уровня, плоскость которых выражается уравнением Z = Л или у = А, -X = А. Меняя параметр Л и организуя цикл, можно вычертить каркас поверхности, состоящий из линий уровня. В уравнении поверхности F {х, у, z) за плоскость линий уровня можно принять г/ = В, тогда каркас обогатится еще одним семейством линий уровня, дополняющим семейство z = Л. Иногда бывает полезно с целью обогащения представления о поверхности перейти от каркаса линий уровня к каркасу из линий, находящихся в заранее выбранных параллельных плоскостях. Рассмотрим геометрическую модель построения такого каркаса.

Пусть поверхность задана каркасом из одного семейства линий уровня. Введем в рассмотрение однопараметрическое семейство взаимно параллельных плоскостей, в которых (рис. 16) должны лежать искомые линии каркаса. Рассмотрим одну из таких плос-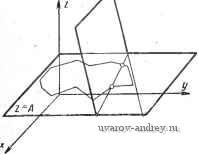

f>0

Рис. 16. Формирование семейства линий каркаса поверхности Рис. 17. Области значений функции f{t\, )

костей А X -\- Б^у + Cz + = 0. Она пересекается с каждой плоскостью линий уровня по прямой, точки пересечения которой с линией уровня легко найти. В каркасе из линий уровня таких точек будет множество. Соединив эти точки в определенной последовательности, получим искомую линию, которая обогащает каркас. В конечном итоге можно получить каркас из вновь введенных линий. Таким образом, алгоритм позволяет на поверхности, заданной каркасом, провести любую плоскую кривую, используя только массивы корней.

2. АЛГОРИТМ АВТОМАТИЧЕСКОГО ПОСТРОЕНИЯ ОЧЕРКА НА ИЗОБРАЖЕНИИ ПОВЕРХНОСТИ, ЗАДАННОЙ ДИСКРЕТНЫМ КАРКАСОМ

Очерк является опорным моментом в зрительном восприятии изображения, поэтому его наличие значительно увеличивает наглядность чертежа. Алгоритмы автоматического построения очерка каркасных поверхностей в литературе не описаны. Опубликованные в зарубежной литературе рисунки каркасов поверхностей, построенные по различным алгоритмам, либо не содержат очерка, либо имеют указания на ручную доработку рисунка при условии очень густого каркаса.

Предлагаемый алгоритм работоспособен при условии кусочно-линейной аппроксимации поверхности. Исходными данными слу--жат массивы вычерчивания линий каркаса. Выходными данными являются массивы для вычерчивания линии очерка, состоящие из точек (их координат), входящих в линии каркаса и расположенных на линии очерка. Линия очерка аппроксимируется кусочно-линейно.

В основу алгоритма нахождения точек очерка положены известные свойства функции / (rj, I), представляющей собой уравнение