Ротативные и спироидальиые поверхности

Ротативной принято называть поверхность, получаемую обкаткой некоторого торса плоскостью с нанесенной на ней образующей. В простейшем случае в качестве торса можно взять цилиндрическую поверхность, образующие которой перпендикулярны к плоскости ху. Уравнение такой поверхности можно записать как уравнение некоторой кривой т, расположенной в плоскости ху : у = у {х). Уравнения плоскостей, обкатывающих эту цилиндрическую поверхность, запишутся как уравнения касательных к кривой т:

У-Уг-{\(-г) (2)

где Xi и Ух - координаты точек касания и = tg

Возьмем в качестве геометрического места конечных точек векторов параллельного переноса кривую п, представляющую собой развертку кривой т, т. е. ее эвольвенту. Пусть, у равнение эвольвенты т имеет вид

y = F (X). . (3)

Решая совместно уравнения (2) и (3), получим непрерывное множество точек N ... (х', у'), каждую из которых можем принять за конечную точку вектора параллельного переноса r \х', у', 0\. В рассматриваемом случае поверхность будет ротативной, т. е. поверхностью обкатки. Поверхности, известные под названием спироидальных, получаются смещением обкатывающей плоскости вдоль прямолинейных образующих обкатываемого торса.

Квазиротативные и квазиспироидальные поверхности. Квази-ротативными мы будем называть поверхности, получаемые из ротативных поверхностей непрерывными смещениями их образующих. В нашем случае, когда обкатываемый торс представляет собой проецирующую цилиндрическую поверхность, квазирота-тивная поверхность образуется непрерывными смещениями ротативной поверхности по горизонтальным направлениям. Отсюда следует, что геометрическое место конечных точек векторов параллельного переноса теперь можно выбрать как произвольную кривую п плоскости ху, задавая ее уравнением.

Уравнения квазиротативной поверхности будут включать х' и у', которые получаются из совместного решения уравнений (2) и (3). Если образующие квазиротативной поверхности подвергнуть смещениям по направлению образующих обкатьшаемой цилиндрической поверхности, то можно получить поверхность, которую называют квазиспироидальной. Свобода выбора кривых тип обусловливает многообразие форм квазиротативных и квазиспироидальных поверхностей. Последнее способствует кон-

струированшо из этих поверхностей разнообразных технических форм.

Заметим, что разнообразие форм поверхностей можно добиваться с'помощью третьего переменного элемента геометрической части определителя, а именно, з*а счет выбора различных по форме исходных образующих I . Выбирая в качестве / прямые линии, будем получать линейчатые поверхности. Если в качестве / взята окружность, то будут получаться разнообразные циклические поверхности и т. д.

Итак, в основу образования поверхностей конгруентных сечений берется: 1) способ задания семейства плоскостей (параллельные плоскости; плоскость пучка; плоскости, касательные к проецирующему цилиндру; 2) способ задания мгновенных преобразований, размножающих начало координат в кривую г векторов г (горизонтальная кривая г, обобщенная винтовая, цилиндрическая винтовая, прямолинейная и т. д.); 3) способ задания исходной образующей / (прямолинейная образующая, круговая образую- щая и т. п.).

Легко усмотреть, что разнообразие условий выбора семейств плоскостей сечения, кривых г и образующих / не исчерпывает всего множества поверхностей с проецирующими конгруентными сечениями. Полученное нами множество поверхностей с проецирующими конгруентными сечениями можно расширить без существенного изменения схемы их образования путем выбора в плоскости XZ не одной исходной образующей I , а некоторого . однопараметрического множества исходных образующих I , ...

Каркасные поверхности зависимых сечений

Каркасными поверхностями зависимых сечений мы будем на- зывать поверхности, образуемые плоскими кривыми, которые можно разместить на плоскости в однопараметрическое семейство. Конструирование таких поверхностей осуществляется по следующей схеме.

1. В координатной плоскости, например в плоскости xz, выбирают некоторую кривую / . Затем эта кривая размножается в однопараметрическое семейство Ф кривых Ii, ... Если исходная кривая I задается уравнением z= f (х), то уравнение семейства кривых (/ ), ... будет включать в себя не только переменную X, но также еще переменный параметр p.

2 = / (Xi, Pi).

2. Каждую из кривых 1с, ... поворачивают вокруг оси г.. на некоторый угол t\ величина которого зависит от соответствующего значения параметра рК Таким образом, имеем равенство

t = {p). . , (4)

Этим вращением семейство Ф кривых (/ ), ... переводится в семейство Ф' сечений {1У, ... некоторой поверхности Ф'. Учитывая, что каждое сечение поверхности Ф' получается из соответствующей кривой семейства Ф вращением, мы можем записать параметрическое уравнение каркаса сечений поверхности Ф':

z=f(i/q,p),y=(tgo.

где t есть переменный параметр, вычисляемый по формуле (4).

3. С помощью некоторой кривой г задают однопараметрическое множество векторов так, чтобы координаты этих векторов

были функциями углов t, ...: г {х {t), у (t), z(t)\. Начало всех - >

векторов,/- выбирается в начале координат.

4. Сечения (), -. поверхности Ф распределяют в простран-

стве путем параллельного переноса на векторы r в поверхность Ф сечений 1\ соответствующих по форме кривым (/), ... поверхности Ф' и кривым {Гу, ... семейства Ф .

Легко записать параметрические уравнения каркаса сечений li поверхности Ф:.

z-zit)==f {Y[x-x{t)?-\-(y-y{t)]\ р);

У - У it) - {tg t) [х-X (t)].

Однопараметрические семейства кривых I могут быть различной природы В частности, если параметр р есть параметр положения, а кривые / получаются одна из другой движением без изменения формы, то будут получаться поверхности Ф конгруентных образующих /, ... От рассмотренных нами выше эти поверхности будут отличаться тем, что в результате обратных операций параллельного переноса и вращения их образующие I, ... переходят не в одну исходную кривую / , а в семейство кривых /,... Семейства кривых I , ... могут быть зависимы в силу того, что они получаются одно из другого некоторыми простейшими преобразованиями: подобия, родства, проективного, квадратичного соответствия и т. п. В соответствии с видом преобразования мы будем говорить о поверхностях подобных сечений, поверхностях родственных сечений, поверхностях коллинеарных сечений, поверхностях сечений квадратичного соответствия и т. д.

Семейства кривых / , ... могут образовываться не простейшими, т. е. алгебраическими преобразованиями, а более сложными, определяемыми изменением параметра р. В этом случае мы будем говорить о поверхностях сечений, зависимых по параметру р. Остановимся на характере линий хода поверхностей зависимых сечений. Зададимся какой-нибудь простой линией хода в семействе кривых Г, ... Пусть этой линией хода является прямая X = х'. Обозначим эту прямую через т . Прямая т преобразуется на поверхности Ф в линию хода т'. При составлении

уравнении линии хода т необходимо опираться на следующее. Каждая линия хода т' получается из некоторой параллели перемещения какой-то точки М' некоторой кривой т путем смещения вдоль оси г на величину h = f {х', р), поэтому линия хода т описывается уравнениями

z-f{x, p) = f{x, р'),

где h = f {х', р'у, р' - фиксированное значение параметра р. При переходе линии хода т' поверхности Ф' в линию хода т поверхности Ф кривая т' подвергается мгновенным параллель-

ным переносам на векторы г. Учитывая изложенное, получаем уравнения линии хода т в следующем виде:

[х - X it)] + [у - у it)]-ixf;

z-fix, p)-zit)=fix, р').

Так как параметр = ф (р), то окончательно

- [ф ip)]} +[У-У[Ч> ip)]} = х'; z-fix, p)-zUpip)]=fix, р'). . .

Частные виды поверхностей зависимых сечений получаются за счет различных способов задания однопараметрических семейств Ф Ц , ...) и выбора векторов параллельного переноса, а также за счет выбора семейств плоскостей, несущих на себе зависимые сечения. Рассмотрим некоторые частные виды поверхностей зависимых сечений.

Непрерывно-топографические поверхности

Это поверхности, несущие на себе непрерывное множество линий уровня. Поверхность определяется заданием проекции се-, мейства линий уровня и законом распределения их в пространстве. Конструируется она следующим путем.

1. В одной из координатных плоскостей, например xz, задается однопараметрическое семейство Ф кривых 1, ... с извест-нь1ми уравнениями г = f (х, р).

2. В пространстве выбирается кривая т (mg), расположенная в плоскости [Л, параллельной плоскости гу и отстоящей от нее на расстоянии, равном а. При таком задании кривая т будет описываться уравнениями у = ц> (z); х = а м проецироваться на плоскость хг в прямую т^, определяемую уравнением х = а. Заметим, что через каждую точку [д, прямой /Па будет проходить единственная кривая / семейства Ф . Это дает возможность установить взаимно однозначное соответствие между параметрами р\ ... кривых ... и координатами z\ ... точек в силу чего за параметры кривых 1{, ... можно принять z, ...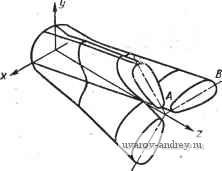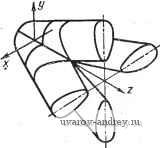

Рис. 11. Непрерывно-топографическая поверхность с тремя раструбами Рис. 12. Непрерывно-топографическая поверхность с четырьмя раструбами

3. Рассматривается множество векторов параллельного пере-

-->

носа Н = М\М', где M - точка кривой т, проецирующаяся в точку М\. Записываются векторы г^- в координатной форме: г [О, Ф(2), 0\.

4. Кривые /г, ... семейства Фа в пространстве распределяются

путем параллельного переноса на векторы г в линии уровня I, ... непрерывно-топографической поверхности Ф. Параметрические уравнения каркаса линий уровня t ... поверхности Ф будут иметь вид

2 = / (л:, р)...; у = Ф

где Z есть некоторая функция от р, т. е. z = F (р).

На рис. И приведено изображение непрерывно-топографической поверхности Ф с тремя раструбами, получаемой путем распределения однопараметрического семейства линий в линии уровня этой поверхности. На рис. 12 приведено изображение непрерывно-топографической поверхности Ф с четырьмя раструбами, получаемой путем распределения кривых однопараметрического семейства в линии уровня.

Поверхности с подобными сечениями

Поверхностью с подобными сечениями называется поверхность, несущая на себе однопараметрическое множество подобных сечений. Конструируется такая поверхность следующим образом.

1. В координатной плоскости, например zx, зададим одно--параметрическое семейство Ф центрально-подобных кривых t ...

с центром подобия в начале координат. Уравнения кривых t , ... могут быть записаны следующим образом:

zk = f (kx); у = О,

где k - переменный параметр, представляющий собой коэффициент подобия.

2. Повернем вокруг оси z каждую из этих кривых t , ... на угол t, величина которого является функцией от соответствующего значения параметра k. Получим поверхность Ф' подобных сечений Г, ... Запишем параметрические уравнения каркаса линий /, ... поверхности Ф':

kz==f{k, Vx+у'У,

у = (tg t) X,

где / = ф (k). Теперь в зависимости от закона задания векторов г параллельного переноса сечений ... поверхности Ф' будем получать различные поверхности Ф подобных сечений t.

Поверхности пучковых каркасов подобных сечений. Возьмем в качестве носителя пучка плоскостей прямую, перпендикулярную плоскости ху и проходящую через точку М (х^, уо). Тогда, уравнение пучка плоскостей будет у - уд = т (х - Xf,), где т - переменный параметр, который можно рассматривать как величину, равную tg /. Зададим далее в плоскости ху кривую п с уравнением у = F (х). В пересечении кривой п с плоскостями пучка получим точки N- каждая из которых будет конечной точкой вектора переноса сечения (/) поверхности Ф' в сечение Р поверхности Ф. Очевидно, что координатами точек N ... будут величины х' и у', полученные в результате совместного решения уравнений

У = Р (х);

У -Уо = т{х - Хо). .

Величина х' будет корнем уравнения F (х) - тх -\-тх - - f/o = 0. а величина у' будет определяться из уравнения у' = = F(x).

Задаемся векторами параллельного переноса r {х', у', 0), координаты которого являются функциями переменного параметра т = (tg t), где / = Ф (k). Параметрические уравнения каркаса поверхности Ф можно записать следующим образом:

... kz-f{ky{x~xr+{y-yr);

. V y-y(ig[cp(k)]){x-x). j

. Если каждую из точек Л^ (х', у'), ... сместить по направлению оси z на величину z = z (x), то уравнения каркаса поверх-

ности Ф, образуемой параллельным переносом сечений (tY на векторы г {х', yz(x)], запишутся так: k[z-z(%)] = /{k, V{x- xf {y- yf);

Квазиротативные и квазиспироидальные поверхности подобных сечений. Выделим в пространство проецирующую цилиндрическую поверхность

У-У{х) (8)

и запишем уравнение проецирующих плоскостей, соприкасающихся с этим и,илиндром:

где -j = tgа t = ff{k). Зададим в плоскости ху геометрическое место концов векторов параллельного переноса сечений V, ... поверхности Ф' в сечении /, ... поверхности Ф. Это геометрическое место представляет собой кривую

y = F{x). (10)

Решая совместно уравнения (9) и (10), получим точки N[ (х', у'), где х' есть корень уравнения F {х) - tx -\- txi - у^, а у' определяется из равенства у' = F (/).

Осуществляя перенос кривых /, ... на векторы r [х, у. О], получим параметрические уравнения каркаса квазиротативной поверхности Ф (/) подобных сечений (6). Смещая по направлению оси Z точки N, ... НЗ величину, равную / = z (х'), получим квазиспироидальную поверхность подобных сечений. Параметрические уравнения каркаса этой поверхности можно записать как уравнения (7). В некоторых случаях однопараметрическое семейство плоскостей, носителей подобных сечений, целесообразно задавать не касательными к поверхности (8), а нормалями к ней. Уравнение соответствующего семейства плоскостей будет иметь вид

Все остальные расчеты осуществляются по приведенной выше схеме.

Поверхности подобных сечений с плоскостью параллелизма.

Поверхности подобных сечений с плоскостью параллелизма конструируются следующим образом.

1. На координатной плоскости, например xz, задается однопараметрическое семейство центрально-подобньщ кривых (/ ) ... с уравнением kz = f (kx), где k - коэффициент подобия.

2. Каждая кривая {t Y вращением вокруг центра подобия (в нашем случае это начало координат) на угол со переводится в кривую (/). Уравнения кривых {Гу, ... составляются с учетом формул преобразования координат при вращении плоской декартовой системы координат вокруг начала координат. Эти уравнения имеют вид

(х sin со + Z cos со) = / /г [л: cos со - Z sin со]}. (11)

Введем в рассмотрение векторы параллельного переноса кривых (/), ... в. кривые поверхности Ф. Пусть это будут-->

векторы r {х = X (к), у = у (к), z = z (k)]. Параметрические уравнения каркаса поверхности подобных сечений с плоскостью параллелизма запишутся так:

/г| [х - X (/г)] sin со + [Z - z (fe)] cos со = = f{k [(х - X (k)) cos со - (z - z(k)) sin CO]); У = У (k).

Если исходное семейство кривых будет распределяться в каркас поверхности Ф без предварительного вращения, то уравнения поверхности Ф примут вид

k Iz-Z (к)] = f (k [х - X {k)]y, . .

у = у (k). -

Если векторы r параллельного переноса кривых исходного

семейства Ф будут расположены по оси у : г' {О, у (к), О], то поверхность Ф будет осевой поверхностью подобных сечений. Она замечательна тем, что ее меридианы (осевые сечения) представляют собой мгновенно-родственные кривые. Вращение кривых исходного семейства вокруг центра подобия можно осуществить и при конструировании пучковых и квазиспироидальных поверхностей перед операцией поворота этих кривых вокруг оси Z. Соответствующие поправки в уравнения поверхностей легко осуществить, учитывая уравнения (11).

Поверхности аффинных сечений

Поверхностями аффинных сечений называются поверхности, несущие на себе однопараметрическое множество аффинных сечений. Рассмотрим один из способов конструирования таких поверхностей.

Зададим в координатной плоскости, например xz, однопараметрическое семейство аффинных кривых ki, kz = f (к^, х),- ... где ку - непрерывно изменяющийся параметр, а feg =

= ср (fej). Повернем вокруг оси z каждую из кривых / на угол

t = F (). Кривые образуют каркас поверхности Ф'. Параметрические уравнения каркаса поверхности Ф можно записать так:

Введем в рассмотрение векторы параллельного переноса, ко-, ординаты которых есть функции от параметра ki.

П \x{ki), y{ki), Z{ki)\.

Распределим в пространстве кривые (/) ... поверхности Ф

->

путем переноса их на векторы г'. Получим каркас кривых ... поверхности Ф. Параметрические уравнения каркаса линий 1\ поверхности Ф запишутся следующим образом:

ih[z-z (i)] = / [ky[x-x{k,)r + [y~y{ki)r];

y-y{ki) = (tgO \x-x{k,)].

Поверхности зависимых линий

До сих пор мы рассматривали способы конструирования поверхностей, несущих на себе зависимые сечения. Ниже изложен более общий метод, когда в качестве зависимых линий поверхности выступают не плоские, а пространственные кривые. Схема конструирования поверхностей зависимых образующих заключается в следующем.

1. В координатной плоскости, например zx, задается некоторое однопараметрическое семейство линий:

z = f{x, р). (12)

2. В пространстве задается поверхность Ф:

y = F {х, Z), (13)

область проекций которой на плоскость zx накладывается на область существования семейства линий (12).

3. Над семейством линий (12) надстраивается множество проецирующих цилиндрических поверхностей. Очевидно, что это множество будет однопараметрическим, и уравнение его совпадает с уравнением (12).

4. На поверхности (13) строятся линии Г, по которым эта поверхность пересекается с цилиндрическими поверхностями (12). Очевидно, что множество линий ... является однопараметрическим, и уравнения этого множества должны быть записаны так:

z = f{x, р);

У = F (х, z). .

5. Задается однопараметрическое множество векторов парал-лельногопереноса линий Г, ... поверхности Ф' в линии /, ... . поверхности Ф. Координаты векторов параллельного переноса берутся зависимыми от параметра р:

Лх(р)\ уШ (14)

6. Множество линий I, ... поверхности Ф' перераспределяется в пространстве во множество линий /, ... поверхности Ф путем параллельного переноса их на векторы (14). Параметрические уравнения каркаса поверхности Ф' запишутся при этом в следующем виде:

Z-Zip)=f[{x-X{p% рП; . . ;

y = y{p)--F[{x-xip% {Z-Z{p))]. . . -

При конструировании поверхностей зависимых линий однопараметрические семейства линий можно выбирать в любой из координатных плоскостей, лишь бы выдержалось условие перекрытия из области существования с соответствующей проекцией поверхности Ф'. Разнообразие форм поверхностей Ф определяется разнообразием семейств (12) поверхностей Ф' и множествами векторов параллельного переноса (14).

Каркасные поверхности топологических преобразований

Мгновенные преобразования. Пусть в пространстве задано некоторое преобразование Г, определяемое уравнениями

х' = fi (х, у, Z, ty,

у' = (х, у, Z, ty, .

z = fs (х, у, Z, t), . .

где t - переменный параметр. Придавая параметру различные непрерывные значения, получим непрерывное мно}кество преобразований Г\ зависящих от параметра t. При осуществлении непрерывного однопараметрического множества преобразований Г', ... размножаем точку пространства в линию, линию пространства в поверхность, а поверхность пространства в непрерывное множество поверхностей, заполняющих отсек пространства. Каждое отдельно взятое преобразование Г^, соответствующее значению параметра называется мгновенным преобразованием.

Мгновенное преобразование переводит точку пространства в точку, линию - в линию и поверхность - в поверхность. Мы будем рассматривать только такие мгновенные преобразования, которые представляют собой топологические преобразования, т. е. когда при переходе от исходной точки к преобразованной ее бесконечно малая окрестность переходит в бесконечно малую окрестность преобразованной точки.