Глава II. ФОРМАЛЬНЫЕ МОДЕЛИ

КАРКАСНЫХ ПОВЕРХНОСТЕЙ

1. КОНСТРУИРОВАНИЕ ЛИНИЙ КАРКАСА. ОПРЕДЕЛИТЕЛЬ И КАРКАС ПОВЕРХНОСТИ

Одним из основных понятий в прикладной геометрии

поверхностей является понятие определителя поверхности. Определителем поверхности называют совокупность условий, задающих поверхность. Поверхность считается заданной, если относительно любой точки пространства можно однозначно решить вопрос о ее принадлежности данной поверхности. Определитель поверхности состоит из двух частей: геометрической и алгоритмической. В геометрическую часть определителя входят геометрические образы и параметры постоянной формы, положения и величины. . Алгоритмическая часть определителя поверхности представляет собой.алгоритм построения точек и линий поверхности, занимающих на ней переменное положение. Например, геометрическая часть определителя поверхности вращения состоит из оси вращения и образующей, имеющих постоянное положение и форму. Алгоритмическая часть определителя этой поверхности задается операцией вращения образующей вокруг оси.

Геометрическая часть определителя линейчатой поверхности состоит из двух направляющих линий постоянного положения и формы, а алгоритмическая часть задается взаимно-однозначным соответствием точечных рядов направляющих линий (с помощью плоскости параллелизма, третьей направляющей, пропорциональным делением хорд направляющих и т. д.).

Постоянные геометрические образы и параметры, задающие алгоритмическую часть определителя, тоже входят в геометрическую часть определителя. Так, плоскость параллелизма или третья направляющая линейчатой поверхности присоединяются к исходным направляющим поверхности как элементы геометрической части ее определителя. Анализ закона образования поверхности имеет своей целью выделение ее определителя. Алгоритмическая часть определителя дает возможность составить формальную модель конструирования непрерывного каркаса поверхности. В фор-

мальнои записи аналитические алгоритмы конструирования поверхности включают в себя непрерывно изменяющиеся параметры. Однако ни на чертеже, ни при реализации их на ЭВМ нельзя до-, биться непрерывного изменения этих параметров: они задаются дискретно. Дискретное множество значений параметров определяет дискретное множество линий поверхности. Это множество линий называется дискретным каркасом поверхности.

В качестве геометрической части определителя поверхности можно назначить некоторый ее дискретный каркас. Тогда алгоритмическая часть определителя включает в себя процесс непрерывного изменения параметров заданных линий, обеспечивающий задание непрерывного каркаса поверхности с исходным дискретным каркасом.

Поверхности, задаваемые непрерывными каркасами, называются каркасными поверхностями. Каркасные поверхности могут, образовываться также путем перемещения в пространстве плоской или пространственной линии неизменной формы или путем непрерывных преобразований исходной образующей. Первые из этих поверхностей будем называть поверхностями конгруентных образующих (иногда их называют кинематическими), вторые - поверхностями преобразований. В дальнейшем под непрерывно изменяющимися величинами будем понимать величины, шаг изменения которых может быть сделан меньше любой как угодно малой наперед заданной величины. Практически это, величины, изменения которых имеют достаточно малый шаг.

Однопараметрические семейства линий

При конструировании каркасных поверхностей бывает необходимо-заранее задавать в координатной плоскости непрерывные однопараметрические семейства линий. Существуют различные методы конструирования таких множеств линий. Одним из распространенных методов решения этой задачи является параметрический метод. Всякая кривая линия определяется некоторой совокупностью условий. Часть этих условий охватывает геометрические образы постоянного положения и постоянных величин. Вторая часть условий определяет способ построения текущих точек по фигуре постоянных элементов. Совокупность условий, характеризующих кривую, называется ее определителем.

Геометрические образы постоянного положения называются геометрической частью определителя кривой, а способ построения текущих точ.ек кривой алгоритмической частью. Например, окружность задается положением центра и величиной, радиуса. Это геометрическая часть ее определителя, а алгоритмическая часть включает в себя способ построения точек, отстоящих от ее центра на расстояние, равное величине радиуса. Параметры, определяющие геометрическую часть определителя кривой, входят в ее уравнение. Алгоритмическая часть представляет собой последователь-

НОСТЬ операций над этими параметрами и координатами точек, задаваемых уравнением кривой.

Например, конхоида Никомеда определяется следующим образом. На расстоянии а от оси у проводится параллельная ей прямая т и задается величина некоторого отрезка /. Через начало координат проводятся всевозможные прямые п, на которых от точек М, ... пересечения их с прямой т откладываются отрезки MN = I. Точки N, ... образуют конхоиду. В уравнение входят два параметра а и /:

{х^ + (л; - af - 1x = 0.

Параметры герметрической части определителя кривой делятся на параметры положения и параметры формы. Изменение первых приводит лишь к изменению положения кривой относительно системы координат, изменение вторых влечет за собой изменение формы кривой.

Прямая линия не имеет параметров формы. Она имеет лишь два параметра положения. Окружность имеет один параметр формы (величина радиуса) и два параметра положения (координаты центра). Все остальные кривые имеют три параметра положения и в зависимости от способа их образования один или несколько параметров формы. Общее число параметров кривой называется ее параметрическим числом. Например, парабола представляет собой четырехпараметрическую кривую. Конхоида Никомеда является пятипараметрической кривой. Она имеет три параметра положения и два параметра.формы. Два параметра положения кривой определяют ее.параллельный перенос на некоторый вектор, а третий определяет ее вращение вокруг точки.

Параметрический метод конструирования семейств кривых. Параметрический метод конструирования однопараметрических семейств кривых заключается в следующем. Кривая задается уравнением, в которое входят параметры положения и формы. Если изменяе^гся параметр положения, кривая будет перемещаться без изменения формы. При изменении параметра формы кривая будет менять свою форму. И в том и в другом случае исходная кривая размножится в непрерывное однопараметрическое семейство, поэтому выбираем один из параметров и, зафиксировав все остальные параметры, подвергаем его непрерывным изменениям. Непрерывному изменению можно подвергать несколько или даже все параметры уравнения кривой. Чтобы получить при этом однопараметрическое семейство, необходимо на изменяющиеся параметры наложить соответствующее число связей. Заметим, что при некоторых способах изменения параметров мы можем получать семейства мгновенно-соответственных кривых некоторых преобразова-

Точное определение мгновенного преобразования см. ниже при описании топологических преобразований.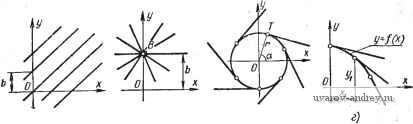

а) 6) В)

Рис. 6. Однопараметрические семейства прямых линий

НИИ. Например, при изменении величины радиуса окружности получаем мгновенно-подобные кривые, при изменении величины одной полуоси эллипса - мгновенно-родственные кривые. Ниже приведены примеры конструирования однопараметрических семейств кривых. Чер'тежи этих семейств приведены на рис. 6-10.

Однопараметрические семейства прямых линий. Прямая линия задается уравнением у = kx Ь, где k - тангенс угла наклона прямой к оси х; b - отрезок, отсекаемый ею на оси у. Зафиксируем значение параметра k. Тогда всевозможным значениям b будет соответствовать множество параллельных прямых, заполняющих плоскость (рис. 6, а). Можно поступить иначе. Зафиксировать значение параметра Ь. Тогда всевозможным значениям параметра k будет соответствовать множество прямых пучка (рис. 6, б).

Однопараметрическое множество прямых можно получить как множество касательных к некоторой кривой. Еслив качестве этой кривой будет взята окружность с центром в начале координат, то множество касательных задается уравнением л; cos а -\- у &\па, - - г = Q, где г.- радиус окружности, а а - переменный параметр (рис. 6, в). В общем случае, когда, кривая задана уравнением У f {х), уравнение множества касательных (рис. 6, г) запишется так:

У~Уг-{-),{х-х,).

Последний способ есть наиболее общий способ образования однопараметрического множества прямых.

Однопараметрические семейства кривых второго порядка. Одним из наиболее простых семейств кривых второго порядка является семейство концентрических окружностей. Если их общий центр расположен в начале координат, то уравнение семейства х^ -\-у^ = г^, где г - радиус окружности есть переменный параметр (рис. 7, а). Можно построить однопараметрическое семейство парабол с общей вершиной в начале координат и общей осью симметрии у. Такое семейство задается уравнением х^ = 2ру, где р -

переменный параметр (рис. 7, б). Если в уравнении эллипса +

= 1 зафиксировать величину полуоси Ь, а величине полу-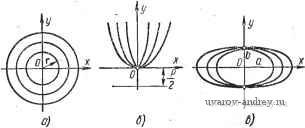

Рис. 7. Однопараметрические семейства кривых второго порядка

ocifa придавать всевозможные значения, то получим однопараметрическое семейство эллипсов с общими вершинами на оси у. При а =1Ь'иы получим окружность. При а < b будут Получаться эллипсы с фокусами, расположенными на оси у (рис. 7, в).

Однопараметрические семейства зависимых кривых. Однопараметрическое множество мгновенных линейных преобразований размножает заданную кривую в семейство линейно зависимых кривых. Рассмотримнекоторые частные случаи таких преобразований. Пусть заданы мгновенные родственные преобразования с общей осью родства k = OAJOAi, где ОА - фиксированный отрезок на оси X. Тогда исходный эллипс с полуосями ОВ и ОА размножится в семейство эллипсов с общей полуосью ОВ и переменными полуосями ОЛ 2, ... Уравнение этого семейства (рис. 8, а)

(0В)2

Можно построить множество эллипсов, мгновенно-родственных эллипсу с полуосями ОВ и ОАх, когда'ось родства есть касательная t в вершине В, а направление родства параллельно прямой t. Задаваясь различными положениями точек А2, ... получим семейство эллипсов, родственных исходному. Заметим, что отрезки ОЛз, ... в этом случае не будут полуосями преобразо-

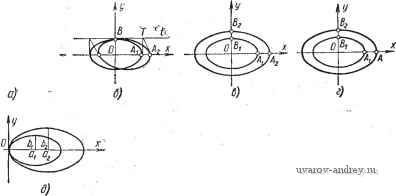Рис. 8. Однопараметрические семейства зависимых кривых

ванных эллипсов. Это видно из того, что касательные к эллипсам в точках AyV. А^, ... должны пересекаться в одной точке Т оси t (рис. 8, б). Можно построить множество мгновенно-центрально-подобных эллипсов с переменными коэффициентами подобия

(рис. 8, в). Уравнение

(kiOAiY

коэффициент подобия k = ~- = -~-

при переменных, но зависимых между собой значениях и будет соответствовать множеству линейно зависимых эллипсов, задаваемых преобразованиями х' = kxr, у' = kx (рис. 8, г). Множество мгновенно-подобных эллипсов можно построить, приняв за центр подобия вершину О исходного эллипса и Ь^. Переменным параметром будет (рис. 8, д).

Однопараметрические семейства кривых высших порядков.

Однопараметрические множества кривых можно конструировать и из кривых высших порядков путем изменения параметров, входящих в их уравнения. Например, кривая, известная под названием верзиера , задается уравнением у (а^ + х^) = а?. Примем величину а за переменный параметр. Получим однопараметрическое множество верзиер (рис. 9, а).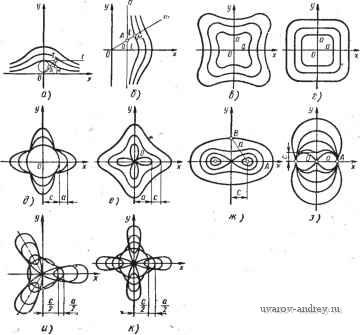

Рис. 9. Однопараметрические семейства кривых высших порядков

Конхоида Никомеда описывается уравнением (д; -f + У^) (х - а) - = 0. Изменяя в уравнении конхоиды величину параметра t, получаем при постоянном а семейство конхоид (рис. 9, б).

Кривая, известная под названием бисквит , задается уравнением х^-]- = а (х^ -- у^). Приняв величину а за переменный параметр, получим множество кривых типа бисквит (рис. 9, в).

Четырехпараметрическая кривая псевдоквадрат определяется уравнением х* -- у* = й*. Приняв величину а за переменный параметр, получим семейство псевдоквадратов (рис. 9, г). Положив в уравнении

переменной величиной параметр а, получим семейство пятипара-метрических кривых шестого порядка (рис. 9, д). Приняв в том же уравнении за переменную величину параметр с, получим другое семейство тех же кривых шестого порядка (рис. 9, е).

Кривая, известная под названием овал Кассини , задается уравнением (х^ -\- у^у - (х^ - у^) = а* - с*. Это пяти-параметрическая кривая четвертого порядка. Положив с постоянным, а а - переменным, получим однопараметрическое семейство овалов Кассини (рис. 9, ж).

Кривая- лемниската Бута задается уравнением (д; + у^) = = + с^у^. При постоянном а и переменном с получаем соответствующее семейство (рис. 9, з).

Уравнению {х^ + yf - а {х^ - Зух) = ---) (д^ +

у^) при G < с соответствует замкнутая кривая, при а = с - трехлепестковая роза с уравнением {х^ -\- yY - а (х^ - Зху^) = = О, при G > с - три изолированных кривых. Положив параметр а постоянным, а параметр с переменным, получим соответствующее семейство кривых (рис. 9, и).

Уравнения кривых можно задавать и в полярной системе координат. Однако после исследования формы кривой, вообще говоря, надо составлять уравнение кривой в декартовой системе координат. Например, уравнению

р* - ар cos 2ф -+= О

при а = о соответствует окружность, при а < с - замкнутая кривая, при а = с - четырехлепестковая роза, при а>с - четыре изолированные кривые. Положив параметр а постоянным, а параметр с переменным, получим семейство кривых (рис. 9, к), уравнение которого в декартовой системе координат имеет вид

{х' + у'-~ + ){х' + у') = аЦх'-уГ

Помимо однопараметрических семейств кривых можно строить однопараметрические семейства обводов.

Конструирование семейств обводов

Обводом называется кривая, составленная из нескольких дуг кривых различных уравнений. Как правило, это многопараметрические кривые. Существуют способы задания единых уравнений обводов, основанные на операции модулирования независимых переменных и их функций. Задав обвод его уравнением, мы можем, как и в обычном случае, изменять какой-нибудь его параметр, получая при этом семейство обводов.

Множество квадратов. Известно, что уравнению д; +11 ~ = а соответствует квадрат с вершинами, расположенными в точках А {а, 0), В (О, а), С (-а, 0), D (О, -а). Если в уравнении квадрата придавать параметру а различные значения, то можно получить семейство квадратов (рис. 10, а).

Возьмем треугольник А (О, а), В {а, 0), С {-а, 0). Его уравнение имеет вид [у -\-\y\ -{-Цх\ -2а\{\у\ + л: - а; + 4- IIд; - а\\ = а. Если в этом уравнении изменять непрерывно параметр а, то получим однопараметрическое множество прямоугольных равнобедренных треугольников ABC, ... с перекрывающимися основаниями АС, ... (рис. 10, б). Уравнению {2х + -1- x) + (% + ilF = соответствует замкнутый обвод, составленный из дуг АВ, ВС, CD, DA, где АВ - дуга окружности

4. у2 - 2. дура gQ дура эллипса х^ +9у^ = 9г^; дуга CD - дуга окружности х^ -j- у^ = 9г^ и, наконец, дуга DA - дуга эллипса 9х^ + = 9г^.

Если в уравнении обвода изменять параметр г, то можно получить однопараметрическое семейство замкнутых обводов (рис. 10, в). Уравнению {2х -\-\х\Y + у^ = 9г^ при х >> О соответствует дуга полуэллипса 9х^ -\- = 9г^ с полуосями г и Зг; при д; <: О - дуга полуокружности -\- у^ = 9г^. Меняя значения параметра г, получим множество объектов, составленных из полуэллипсов и полуокружностей (рис. 10, г).

Уравнению (д; + д;) + (У + \У\У = соответствует при х^О, у > О дуга окружности 2. ри х <0, у >

i> О - луч прямой у = г; при х <0, у <0 уравнение не имеет смысла; при л; > О, у <0 - луч прямой х = г. Переменному параметру г будет соответствовать множество незамкнутых .обводов (рис. 10, д).

Уравнению х^ у\у\ = соответствует при у О дуга окружности х^ + у^ = при у < О - две дуги гиперболы х' -\- У^ = г^. При изменении значений параметра г получаем семейство подобных обводов с центром подобия в начале координат (рис. 10, е).

Уравнению у - b = \ х - 1 4-x - 2 -\-\х - 3 при b = = О соответствует ломаная с вершинами А (1, 3), В (2, 2), С (3, 3).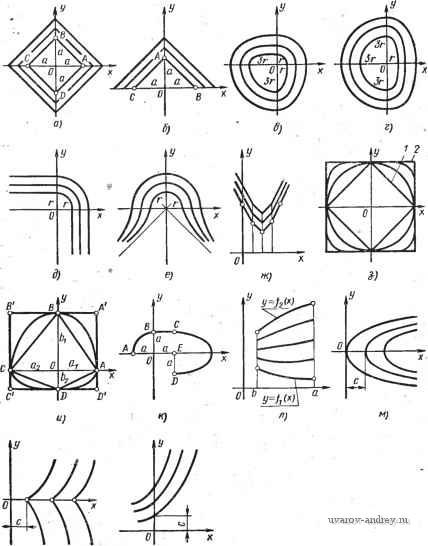

Рис. 10. Множество обводов

Начальным и конечным звеном ломаной являются лучи прямых у=---х-\-&ку=- X - 6, исходящие соответственно из точек

А к с. Если изменять значение параметра Ь, то можно получить семейство параллельно смещаемых обводов (рис. 10, ж), Возьмем два квадрата: один - с уравнением!л; +\у\ = 1. Другой с уравнением 1а; -+\х\ + \у\ = 2. Кривая с уравнением \х\Р +\у\р =1 при переменном р, пробегающем значе-

ния оо < р < 1, занимает всевозможные промежуточные положения между указанными выше квадратами, и при р->1, стремится к первому квадрату, а при р Ьо - ко второму квадрату. При р = 2 получаем окружность, при р = 4- псевдоквадрат (рис. 10, з). Введя в рассмотрение величины

можно показать, что уравнению х' + у' =1 соответствует четырехугольник А (а^. О), В (О, bj), С {-а^. О), D (О, -Ь^), а уравнению х' - I11 + U I + \У'\ =2 - прямоугольник А' ( 1, &j); В' (-йа. bi); С {-а^, -Ь^); D {йу, -Ь^). Уравнению Ixl -blyl Ри переменном р, пробегающем значения оо>р>1, соответствуют кривые, расположенные между четырехугольником и прямоугольником. При р 1 кривая приближается к четырехугольнику ABCD и при р оо - к прямоугольнику А'В'CD. При р = 2 получаем обвод, составленный из четырех дуг различных эллипсов (рис. 10, и).

Введем в рассмотрение функцию S [F (х)], которую определим так: F{x)0- S [F (х)] = +1 и F (х) <0 S [F (х)] в действительной области не определена. Очевидно, что уравнению у ==S {х - а) f (х) соответствует та часть графика кривой у = f (х), для точек которой х > а; уравнению у = {а-х) f (х) - часть графика кривой, для точек которой х а; уравнению у = S [(х - Ь) {а - х)] f (х), где b <а - часть графика кривой, для точек которой b х <. а. С помощью введенной функции можно записывать уравнения достаточно сложных обводов путем объединения уравнений их дуг. Если обвод задан вершинами А {-а. О), В (О, а), С {а. О), D {а, -а), Е (а. О), где АВ - дуга окружности у = - х\ ВС - отрезок прямой у - а; CD - дуга полуэллипса а -Ж - отрезок прямой х = = а; ЕА - отрезок оси, то уравнение такого обвода можно пред-, ставить в следующем виде:

[S [(X + (О - X)] {у - V)] \S [(X - 0) (а - X)] (у - \)\; 8{{х-а){Ы-х)\[ + -\]\8{(у + а)ф~у)\ х X (X- 1)} \S [(X + а){а- х)\ {у - 0)} = 0.

Изменяя параметр а, мы получим семейство подобных обводов ABCDE (рис. 10, к). Тот же самый обвод, если начало координат поместить в точку Е, можно размножить в семейство подобных и не пересекающихся обводов. С помощью функции S {F {х)]