


 |
 |
 |
|
Главная страница » Электрика в театре » Алгоритмы многогранных поверхностей 1 2 3 4 5 6 ... 23 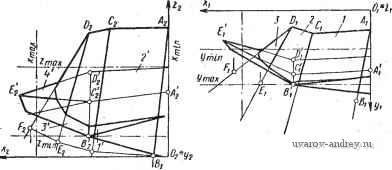 Рис. I. Пересечение г,!исгогп£н,-1ЫХ поверхностей является область наложения друг на друга проекций пересекающихся поверхностей). В рассматриваемом примере такими ограничивающими поле задачи прямыми будут: Ут1п = 26; ys,ax = 48; mln 4, Zinax = 59. Схема алгоритма построения линии пересечения многогранных поверхностей приведена на рис. 2. Изложим некоторые подробности, которые необходимо учитывать при машинном пррграммировании. Таблица 3 Кодировочная таблица
рис. 2. Схема алгоритма построения ликии пересечения многогранных поверхностей: /, - счетчик граней; Jz - счетчик поверхностей; п, - число граней поверхности: g - 1-я грань Начало) Формирование п, по 3, r-EO Выделение Вершин Врана с№3, - F0---3 Вычисление коэ/рфици- ентоВ уравнения GoI-, Размещение коэсрфици- ентоо В памяти
Расчет координат точен линии пересечения 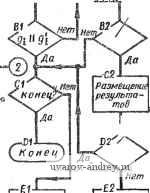 Решение годно? J Коиец по упарв еранеиЧ Переадресация перебора изменение параметроб расчета 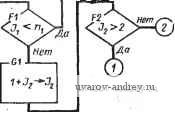 В случае частного положения одной, либо обеих пересекающихся плоскостей соответствующие коэффициенты их уравнений будут равны нулю. Формулы определения координат точек, принадлежащих проекциям искомой линии, записанные в явной относительно X форме, выглядят следующим образом: Ck В, m г- т А -ёг. т--п При рассмотрении формул видно, что они вызывают аварийный останов машины из-за операции деления на ноль в следующих, например, случаях: = 0; =0; = 0; Л„ = Л^, = 0. Отсюда видно, что, программируя алгоритм, необходимо предусмотреть дополнительные логические проверки во избежание остановки решения в некоторых частных случаях. Указанные проверки не нужны, если тривиальные случаи расположения плоско-. стей определить при кодировании и отбросить их, так как решение в этих случаях находится графически весьма просто. В таблице результатов (табл. 4) приведены результаты машинного решения задачи (см. рис. 1). Алгоритмическое разрезание многогранной поверхности в процессе ее развертывания. Построение развертки многогранной поверхности в процессе ее развертывания является типичной метрической задачей. Операция развертывания предполагает разбиение поверхности на многоугольники и разрезание полученной сети по ее ребрам. При этом допустимо, чтобы разбиение охватывало не только сетку многогранника, и тогда возможно бесконечное множество разверток одной и той же поверхности. Связной назовем развертку, которая не распадается на несколько кусков. Многогранная не ветвящаяся поверхность формируется из связной развертки сгибанием последней по некоторым линиям до отождествления тех ребер, которые должны быть склеены . Связные развертки важны с точки зрения практики вследствии технической неравноценности операций сгибания .и отождествления. В силу этого оптимальной может быть т&кая развертка, в которой суммарные длины ребер, требующих операций разрезания и сгибания, находятся в определенном отношении (например, когда выгодно иметь минимальную длину разрезаемых ребер либо наоборот). Ниже кратко изложена формальная модель разрезания поверхности с целью ее развертывания и построения развертки автоматически с помощью ЭВМ. Результаты машинного решении задачи (см. рис. I) Таблица 4
1. Пусть относительно развертываемой многогранной поверхности известно следующее: а) координаты вершин; б) условия инцидентности вершин и граней. Ребро определено при этом парой вершин, инцидентных паре смежных граней. Пусть поверхность имеет границу, состоящую из ребер, которые являются результатом пересечения поверхности с некоторой пустой гранью. Пусть i = I, 2, k есть признак связности границы. Ребро, инцидентное пустой грани, а вершину, инцидентную такому ребру, назовем граничными. Внутренней будем считать вершину, которая не инцидентна (не связана) граничным ребрам. Ребро, связывающее только внутренние вершины - внутреннее. Грань может не содержать ни одного граничного ребра, а может содержать только их. В первом случае грань назовем внутренней, во втором - изолированной. Наконец, отгибаемой будем называть грань, которая может быть повернута около одного из ее ребер либо вершин без дополнительных операций. Разрезание поверхности полагаем состоящим из отдельных разрезов, выполняемых в пределах полного ребра и ведущих к появлению граничных ребер. В этом смысле разрезание, например, внутреннего ребра не является разрезом. Внутренние вершины можно различить между собой по числу разрезов, которые необходимо сделать, чтобы вершина стала граничной. Это число назовем порядком вершины. Очевидно, что признаком отгибаемой грани является отсутствие внутренних вершин, инцидентных ей, поэтому для развертывания поверхности достаточно все ее вершины превратить в граничные путем разрезов. Пусть имеется одна внутренняя вершина, для превращения ее в граничную достаточен один разрез. Если на поверхности имеется вершина порядка п, то для превращения ее в граничную необходимо сделать п разрезов на р^рах, которые не являются внутренними. Поскольку поверхность имеет границу, всегда можно отыскать вершину, порядок которой равен 1. От нее по внутреннему ребру можно прийти к вершине с п = 2 и так далее до вершины с = п. Таким образом, при разрезании поверхности с границей i = 1 минимальное число разрезов равно числу внутренних вершин. Сказанное позволяет изложить правила разрезания поверхности при ее развертывании: а) выделить внутреннюю вершину поверхности с м = 1; б) выделить ребро, ведущее к указанной в п. а вершине и не являющееся внутренним (можно поставить еще условие максималь- ности либо минимальности длины ребра); в) выполнить разрез по выделенному ребру; г) проверить, имеются ли еще внутренние вершины (если да, то процесс повторяется с п. а, в противном случае задача разрезания решена). 2. Рассмотрим теперь поверхности, не имеющие границы, либо С границей, характеризующейся признаком i ф I. Пусть задан Распознавание границы Формирование признака связности P=i -Б 0-1- Обзор ходов вершин поверхности Нет Выделение Коней, по \дершинам? Нет Формирование массива результатов Рис. 3. Схема алгоритма гогранной поверхности разрезания мно- (рерывйни многогранник. Будем считать одну из вершин его границей, стянутой в точку. Признак такой границы будет t = 1, так как окрестность внутренней вершины гемеоморфна кругу. Но тогда справедливо следующее утверждение: число разрезов, минимально необходимое для развертывания многогранника равно числу его вершин без одной. Для решения вопроса о разрезании поверхности с границей i ф 1 необходимо уточнить понятие границы. Границей поверхности будем называть такой разрыв, который невозможно заклеить кусками плоскостей без появления внутренних вершин. Разрывы, не являющиеся границей, назовем окнами . Пусть имеется поверхность с границей связности К. Это означает, что у поверхности отрезаны по меньшей мере К внутренних вершин (отрезано может быть и больше, но это роли не играет, так как вместе с вершинами отрезана и необходимость отгибать соответствующие грани при [развертывании; однако грани, сходящиеся к части границы, представляющей собой односвязную область, повторяют ситуацию, имеющуюся в окрестности любой внутренней вершины). Поэтому для развертывания необходимо предусмотреть один разрез на каждый такой случай. Если граница поверхности состоит из К областей, каждая из которых односвязна, то считая одну из областей за границу поверхности с признаком t = 1, нужно вычислить необходимое число разрезов и добавить к ним /С-! разрезов. Схема алгоритма, реализующего изложенную формальную модель, приведена на рис. 3. Символ F0 включает выделение ребра, инцидентного рассматриваемой вершине и не удовлетворяющего критерию оптимальности (max или min длины). Символ J0 включает выделение i - 1 ребер (в поверхности с t-связной границей), проходящих через вершины, принадлежащие различным областям границы.- нет выделение ребер 5. АЛГОРИТМЫ РЕШЕНИЙ МЕТРИЧЕСКИХ ЗАДАЧ НА ЧЕРТЕЖЕ Координатный метод решения задач. При работе с чертежом усилия конструктора направлены к наиболее целесообразному размещению частей конструкции в пространстве. При этом наиболее часто приходится решать метрические задачи двух типов: во-первых, построение истинной величины плоской фигуры, за-, данной на чертеже проекциями; во-вторых, определение формы и величины проекций фигуры, заданной в пространстве некоторыми параметрами. Для краткости в дальнейшем будем условно называть первую задачу прямой, а вторую - обратной метрическими зада-. чами. Плоскость, в которой решается метрическая задача, назовем полем задачи. В нашу задачу входит построение формальной модели решения, которое было бы пригодно для обоих типов метрических задач. В качестве основ формальной модели возьмем общеизвестное положение о том, что операция параллельного проецирования выполняет аффинное преобразование координат. Это и другие виды преобразований используются в прикладной геометрии давно. Рассмотрим графическую модель решения метрической задачи. Пусть полем задачи является плоскость, заданная на чертеже проекциями точечного базиса: А у, В^, и Л 2, В2, (рис. 4). Введем в плоскости ABC прямоугольную систему координат х', у' с началом в некоторой точке О' (01, Ог). Проекции этой системы х[; у\ и х'2, у'г будут находиться с ней самой в родственном соответствии. Будем называть систему х'у' местной в отличие от базовой хуг. Для построения любой из проекций местной системы координат достаточно определить угол между проекциями осей и коэффициенты искажения масштабных единиц вдоль них. В дальнейшем операции по построению проекции местной системы назовем аксонометризацией поля задачи. Проведем оси координат параллельно главным^ направлениям родственного преобразования поля задачи в одну из проекций, например в Л^, В^, Су. Такими направлениями являются горизонталь и линия наибольшего ската плоскости ABC. Масштабные единицы вдоль полученных осей 0\х\ и О^ух можно построить, используя нормаль О'N к плоскости ABC с основанием в точке О' (01, 62). Истинная величина отрезка нормали строится поворотом его около оси, проходящей через О' перпендикулярно плоскости Оху. Символом я]) отмечен угол, который плоскость ABC составляет с Оху. Отложив на ОгЛ/г, выражающем истинную величину отрезка нормали, натуральную масштабную единицу О'Е и спроецировав ее на вертикаль, получим О'чВу, которая служит единицей измерения вдоль оси 0\у\. Вдоль оси 0хх\ действует неискаженнаянатуральная единица. Реализуя обсуждаемые операции, мы задаем на плоскости ABC ортогональную сеть, линии которой параллельны главным направ- 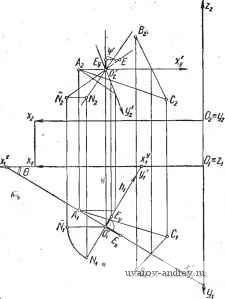 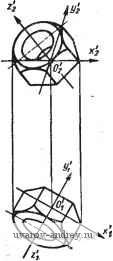 Рис. 4. Графическая модель решения метрической задачи Рис. Б. Пример решения метрической задачи в трехмерной области лениям родственного преобразования, устанавливаемого ортогональным проецированием плоскости на одну из координатных плоскостей базовой системы. При этом сетевой угол сохраняется равным 90°. Для решения прямой метрической задачи в поле 01, х[, у\, например, достаточно растянуть сеть вдоль оси Olyi с коэффициентом растяжения, равным 1/cos я]). Для решения обратной задачи необходимо сжатие вдоль той же оси с коэффициентом, равным cos я]). С помощью изложенной модели, используя аппарат аналитической геометрии, можно решать самые различные конструктивные задачи, например, строить проекции различных кривых общего положения по уравнениям. В рамках рассматриваемой модели можно решать метрические задачи в трехмерной области решений. Решение задачи на построение ортогональных проекций гайки, за-данной своими размерами и положением оси в пространстве, отнесенной к базовой системе xyz, иллюстрируется рис. 5. Все построения, связанные с третьей осью Oz местной системы координат, ничем не отличаются от изложенных ранее. Последнее обстоятельство удобно с точки зрения использования циклов в машинной программе, реализующей обсуждаемый способ. Предлагаемый способ решения достаточно универсален и удобен для машинного решения, так как координатный способ особенно тесно связывает графические операции с аналитическими, что облегчает построение их вычислительных эквивалентов. Положи- тельным фактором координатного .метода является задание общего закона преобразования поля задачи, выводимого кз исходных данных алгоритмически. Это сокращает число исходных дан- ных. Формальная модель координатного способа. Формальная модель координатного способа получается следующим образом. Если плоскость ABC задана, например, координатами точечного базиса в системе xyz и введена местная система х'у' (рис. 4), то необходимо знать формулы преобразования координат из базовой в местную систему. Используем известные в аналитической геометрии выражения %-01 Ui - Ув1 - sin ( cos ( cos e - sin e sin e COS e
Они легко приводятся к виду . : xl = (xi -Xoi)cose + (f/i + f/oi)sin6; yi = - (xi - xoi) Sin e + (f/i - yi) cos e, , где Xoii/oi - координаты начала местной системы относительно базовой ХхУх (рассматриваются горизонтальные проекции); 6 - острый угол между осями 0ix\ и 0 Ху. Если имеются коэффициенты А, В, С, D уравнения плоскости поля задачи, то легко заметить, что В/А = ctg 6, но тогда slne = cos 6 = Полученные величины используем в формулах преобразования. Определим положение осей местной системы координат. Ось OlXi проходит через начало OJ (ХдУо), которое задано исходными данными. Уравнение этой оси в базовой системе У1~ Уо = k {х - Хо), где k = -А/В, так как ось О'х' в пространстве параллельна плоскости Оху. Положим теперь в уравнении оси yi = О, тогда Точки ХоУо и х^О определяют ось 0[х'у Можно, конечно, вычислить у^, положив в уравнении оси О'х' - Xi = 0. Ось 0[у[ определяется уравнением У1~ Уо =--F - где k = -А/В. . Положив в этом уравнении у^ = О, получим ХУ = -+Х,. Ось 0[х[ определяется, таким образом, точками ХоУо и х^О. Используемые отрезки, которые отсекаются осями местной системы координат на гдризонтальной проекции от оси абсцисс базовой системы, легко построить на чертеже. Обратимся теперь к вычислению величин масштабных единиц вдоль осей координат местной системы (горизонтальная проекция). Для общности условимся в дальнейшем считать, что осями, параллельными базовым плоскостям xOf/,xOz й yOz будут в местной системе выбираться оси О'х', О'у' и Oz соответственно. Таким образом, при решении метрической задачи на проекции, снабженной индексом 1 (вид сверху), ось О'х будет горизонталью; в случае использования вида спереди ось О'у' - фронталью и т. д. Тогда масштабная единица, откладываемая вдоль оси местной системы, которая является линией уровня, будет равна натуральной единице. Вдоль второй оси, совпадающей с линией ската, масштабная единица El = Ei cos я]), где Et - соответствующая натуральная единица, ijj - угол, который заданная плоскость составляет с координатной плоскостью базовой системы, проецирующейся на данной проекции без искажения. Величину cos я]) можно определить по известной из аналитической геометрии общей формуле ЛИг + filfiz -f С1С2 COS я]) KЛf-f в? + с? КЛЦ-ВЦ-С1 Для случая, изображенного на рис. 3, С08Я]5 = с Все изложенное составляет формальную модель решенияпря-мой метрической задачи. Обратимся теперь к рассмотрению формальной модели обрат- ной задачи. Ее особенности проявляются при рассмотрении исходных данных. Последние должны включать в себя параметры, определяющие натуральную форму фигуры и ее положение в пространстве, отнесенном к базовой системе. Такие параметры могут быть выбраны различным образом, поэтому необходимо остановиться на удобном с точки зрения машинного программирования и типичном для процесса конструирования наборе. Известно, что форма фигуры определяется координатами некоторого множества принадлежащих ей точек в местной системе координат, связанной с фигурой. Такой процесс определения фигуры с точностью до ее движения в пространстве называется внутренней параметризацией. Положение местной системы координат определяется некоторыми параметрами относительно базовой системы (внешняя параметризация). При нанесении размерной информации на чертеже конструктор пользуется именно этими системами. Условимся о параметрах, определяющих местную систему координат. Зададим координаты начала. Так как на одну из осей наложено ограничение быть линией уровня, то проще всего задать угол наклона этой оси по отношению к одной из осей координатной плоскости базовой системы, параллельно которой взята линия уровня. Задав далее cos я]) угла наклона плоскости поля задачи либо угол ijj (имеется стандартная подпрограмма вычисления тригонометрических функций), мы определим положение местной системы. Большая часть формальной модели, работающей в режиме решения прямой задачи может быть использована и для обратных метрических задач. Необходимо предусмотреть оператор, сжимающий местную систему по одной из осей с коэффициентом сжатия, равным cos я]). Для того чтобы результаты решения можно было выдать в виде координат в базовой системе, воспользуемся формулами перехода x = xiCosQ - у[ sin6; у = xl sin yl cos 6, где yl = у' cos я]) в случае решения обратной задачи и у[ = = у'/cos яр - в прямой задаче; угол 6 - показан на рис. 4. Изложенное позволяет разработать единый алгоритм решения метрических задач обоих типов. Наконец, сделаем некоторые дополнения для решения задачи с трехмерными фигурами. Для этого необходимо дополнительно определить величину масштабной единицы вдоль оси 0[z[. Легко видеть, что последняя выражается формулой Е'с = Ее sin яр, Преобразования по этой формуле аналогичны тем, которые применяются в прямой задаче, поэтому они могут быть легко программированы в виде цикла.- 1 2 3 4 5 6 ... 23 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2000-2025. Поддержка сайта: +7 495 7950139 добавочный 133270.
Заимствование текстов разрешено при условии цитирования. |