на пересечение поверхностей автоматически с весьма небольшим массивом исходных данных.

Отметим, что предлагаемый путь решения не является единственным. После введения z = hi и приведения системы уравнений к соответствующему виду можно применить один из известных методов решения нелинейных систем. Однако большинство таких методов, несмотря на применение развитого математического аппарата, требует в качестве исходных данных некоторого приближённого значения искомого корня. Это обстоятельство в условиях решения поставленной задачи приводит к дополнительным затруднениям, так как приближенные значения корней ищутся чаще всего графическим методом, который мы стремимся устранить из решения. В предлагаемом же способе корни задаются с точностью до поля решения.

Предлагаемый ниже способ рассчитан на более узкое применение, но более .прост и удобен для использования в задаче на пересечение поверхностей в условиях, когда заранее неизвестно, какого рода корни будут в данном сечении. Приведем некоторые предварительные рассуждения. Рассмотрим функцию Ajf, =

= fih,), где д% = е!--ег.

в обсуждаемой задаче можно составить до четырех таких функций. Имея в виду регулярность кривых, выражаемых исходной системой, можно считать, что при уменьшении абсолютного значения происходит приближение к корню системы, а при увеличении - удаление от корня. Далее, так как кривые односвязны, за исключением гиперболы, то можно считать Лу/, непрерывной в промежутке [hj-; /ly+il при условии вещественности ее значений на границах промежутка. В случае гиперболы этот промежуток не должен превышать расстояния между вершинами ветвей гиперболы. Это расстояние всегда может быть определено, если имеется уравнение гиперболы. В дальнейшем будем считать шагом параметра величину б^+i = \hj - hj+i .

Будем управлять шагом параметра в соответствии с ходом изменения функции Ау с помощью некоторых управляющих функций б = Ф^,. (Ayft), где Ф^ - управляющая шагом функция (i = 1, 2, так как функций может быть несколько). Регулирование процессом с помощью управляющих импульсов, формируемых в результате отклонений процесса от некоторого заданного уровня, можно отнести к цепи обратной связи.

Сформируем теперь управляющие функции для различных ситуаций задачи. Будем проверять на каждом шаге знаки функций Лу/,. Из первой теоремы Коши следует, что если sign Ау/, ф sign Д(/+]) ft, то в промежутке Ikf, hj+i] имеется, по крайней мере, одна точка, в которой Aj = О, что соответствует корню вида Ki исходной системы. Приближение такого корня можно осуществить методом пропорционального деления промежутка, то аналогично линейной интерполяции и соответствует методу хорд. Эффективность такого метода с точки зрения точности и

Рис. 22. Ситуация пересечения кривых

Рис. 23. Ситуации с корнями различной кратности: а - случай отсутст'вия корней;, б- отсутствие четно-кратного корня

о

fmin

max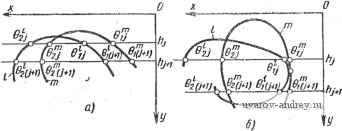

сходимости известна. Рассмотрим рис. 22. Если на границах промежутка [hj-, hj+i ] справедливо Aj-h = 6fy - 62), u+i) h = = e{ (/+1) - ef(/+i), причем sign A/ft sign Д(у+1) ft, то, применяя метод пропорционального деления промежутка, можем записать

Ayft . . .

Вычисляемый шаг параметра

В дальнейшем изложенный случай, приводящий к применению процесса деления промежутка, будем обозначать символом Ф^.

Теперь возьмем случай, когда на границах промежутка [hj-, выполняется равенство sign A,-ft = sign A(y+i) л. В рассматриваемом промежутке при этом может не оказаться корней (рис. 23, а). Однако уверенно констатировать это можно по отношению только к нечетно-кратным корням. На рис. 23, б изображена ситуация, при которой в промежутке не обнаружен четно-кратный корень. Таким образом, информации о знаках функций Ayft на границах рассматриваемого промежутка недостаточно для обнаружения в промежутке четно-кратного корня.

Рассмотрим механизм, позволяющий отличать промежуток, в котором наверняка не имеется четно-кратных корней, от промежутка, в котором они не исключены. Пусть (рис. 23, б) имеются

две прямые у = hj и у - /ly+i. Будем называть /-й шаг предыдущим, а (/ + 1) - текущим. Для удобства рассмотрения изолируем функцию Ajh = Qij - 6?) и покажем ее на рис. 24. Отметим, что если в промежутке [hf, четно-кратный корень имеется, то монотонность функции Ду, безусловно, нарушается. Однако нарушение монотонности Ду не является достаточным условием наличия четно-кратного корня, так как может быть следствием, например, простого сближения кривых без касания с последующим удалением их друг от друга. Четно-кратный корень будет нами отмечен только в случае, когда минимальное расстояние между кривыми будет меньше е с точностью, до которой -вычисляется корень. Рассмотрим еще r]y i шаг (будем называть его граничным). Тройку значений функций Ду/ соответствующих граничному, предыдущему и текущему шагам, будем называть триплетом. С каждым новым шагом будем переводить бывший текущий шаг в предыдущий, а предыдущий в граничный шаг. Таким образом, на каждом шаге рассматривается новый .триплет. Будем называть такой процесс скользящим триплетом. Пусть на рис. 24 исходным является триплет, образованный прямыми у-2, hj i и hj шагов. Каждый новый шаг будем считать шагом .скользящего триплета.

Утверждение. Один шаг скользящего триплета позволяет обнаружить нарушение монотонности функции Ду в случае неизменности ее знака.

Доказательство. Рассмотрим значение функции Д на исходном триплете. При переходе от hj i и Яу существуют следующие возможности: а) Д(у 1) h = Дул; б) Д(у 1) л > Дул; в) Д(у 1) ft < Дуй. В случае а) рассматриваемые два значения позволяют обнаружить нарушение монотонности вследствие очевидного факта отхода кривой в промежутке lhj i, hj ] от прямых, .соединяющих граничные точки промежутка попарно. В случаях б) и в) включим в рассмотрение значение функции Д(у- 2) л на граничном для исходного триплета шаге бу 2. Тогда появляются следующие возможности: а) Д(у 2) h = Д(;-1) н; б) Д(у-2) н > Д(/-1) h] в) Д(у 2)й < Д(у 1)й. Случай а) был- разобран выше, следует только отметить, что если Д(у 2)й = Д(у-i)ft, то не может быть Д(У 1) ft = Ду, так как мы рассматриваем кривые второго порядка. Но тогда A(y i)ft<Ayft. либо .Д(у 1) ft > Ayft. Легко видеть, что в первом случае имеем в промежутке lhj 2, hj i] некоторый минимум Akh, а во втором - некоторый максимум. Пусть Д(у 2) ft > Д(у 1)й, тогда может случиться, что Ajf, < < Д(/ 1) h либо Ajfi > Д(у 1) ft. Первая ситуация не позволяет обнаружить нарушения монотонности Ajf несмотря на то, что корень вида fC может быть пройден, как это показано на рис. 24. Вторая ситуация характерна тем, что нарушение монотонности обнаружено. Будем говорить в таких случаях, что триплет действовал. В данном случае действовал исходный триплет.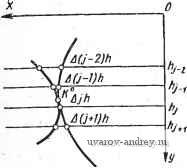

Рис. 24. Случай четно-кратного корня Рис. 25. Ситуация с дроблением шага

Пусть возникла первая ситуация. Сделаем шаг скользящим триплетом. Снова рассмотрим получившиеся случаи. Если корень был пройден, то значение A(/+i)ft > А/л, т. е. А/й начнет увеличиваться, и нарушение монотонности будет обнаружено на этом первом шаге. Если, наконец, рассматривать возможность в), при которой A(/ 2)ft < A(/ i)ft, то могут возникнуть ситуации, аналогичные изложенным, и нарушение монотонности будет обнаружено либо на исходном триплете, либо на первом шаге скользящего триплета.

Изложенное доказывает утверждение.

Обнаружив промежуток с нарушением монотонности А/, будем применять формулу деления промежутка, а случай действия триплета обозначим символом Ф^.

Выше была проанализирована ситуация, которая характеризуется наличием только двух прямых у = hj, однако при этом нарушение монотонности не вызывает сомнений. В таком случае (обозначим управляющую функцию символом Ф^1) необходимо, не образуя триплета, переходить к использованию формулы деления промежутка. К Ф^,1 отнесем л-акже ситуацию, которая возникает в начале решения задачи, когда прямых у = hj проведены только две. Функции А/ вычислены, и знаки их на границах промежутка совпадают. Триплет, образованный с помощью внутренней прямой по формуле деления промежутка, обеспечит в случае наличия в промежутке корня более быструю сходимость процесса приближения, так как промежуток будет более узкий, чем в случае, когда триплет образован с помощью внешнего шага.

До сих пор мы предполагали, что функция имеет вещественные значения на обеих границах рассматриваемого промежутка. Однако легко представить себе ситуации, в которых некоторые или даже . все функции А , не имеют вещественных значений на одной или на обеих границах промежутка. Как показал опыт, подобные ситуации характерны для начальной и конечной стадии решения задачи.

Пусть, например, возникла ситуация, показанная на рис. 25. Разделим промежуток [hf, /ly+il пополам и сделаем внутренний шаг

S -

0(/+2)вн - -2

Внутренняя прямая у - /1(у+й)вн может пройти так, как показано на рисунке, однако hj+k) вн могло оказаться и большим, чем ординаты корней, заключенных в промежутке, поэтому из получившихся двух промежутков [hj, /Ib 1 и [/ly+i, h} выберем тот, который повторяет исходную ситуацию (на рис. 25 таким будет промежуток [hj, ha]), и продолжим применять формулу деления промежутка. Этот процесс продолжается до тех пор, пока величина внутреннего шага не станет б(у4- ) вн £ После этого берется та из прямых, у = вн, на которой имеются вещественные значения А(/+п) вн, и исходная прямая {у = hj+i на рис. 25). Дальнейшее решение проводится, исходя из двух прямых, аналогично случаю Фух.

Процесс, направленный на вырождение промежутка, в котором на.одной из границ функция Ау не имеет вещественных значений, легко себе представить и для ситуации, которая возникает, если на рис. 25 прямые hj и hj+i поменять местами. Случаи, аналогичные рассмотренным, будем обозначать символом Ф^. Рассмотрим теперь ситуацию, представленную на рис. 26. Функция Ау не имеет вещественных значений на обеих границах промежутка [hj, hj+i]. Изменим прямую у = hj на прямую х = /гу с изменением соответственно границ поля задачи. Эта мера поможет свести рассматриваемую ситуацию к изложенным выше. Однако необходимо считаться с возможностью ситуации, показанной на рис. 26, б, в которой изменение прямой не привело к улучшениям. В последнем случае необходимо восстановить исходную ситуацию с прямой y = hj и применить формулу деления промежутка. Этот случай обозначим символом Ф^5. Он отличается от Ф^4 тем, что число корней е'у на границах промежутка [hj, /ly+il одинаково.

Рис. 26. Изменение секущей прямой: с - успешное; б - безуспешное

hj+,

Рнс. 27. Ситуация с рассмотрением двух промежутков

На рис. Т1 изображена ситуация, которая также подходит под случай Ф^б- При введении внутренней прямой у = /i(/-i-n) вн могут образоваться два промежутка, у которых на общей границе А(/+/1)вн вычисляются вещественные корни и значения A(/+ft) вн, а на других границах вещественных корней и значений А не будет вовсе (см. рис. 26, а), либо они будут отличаться по индексу от Д(/+п) вн (рис. 27). Этот случайявляется как бы сдвоенным Ф^ и требует рассмотрения обоих промежутков: [/1(л- )вн; hj\ и [/!(/+ )вн; Обозначим этот случай символом Фуб-

Таким образом, нами рассмотрены: случай, в котором функции Дуй существуют, на обеих границах промежутка и различаются либо не различаются по знакам; случай существования Ду не в полном количестве; случай полного отсутствия на одной либо на обеих границах промежутка [/ly, /ly+iJ. Все рассмотренные альтерйативы сведены к двум формулам деления промежутка. Различные случаи применения этих формул отличаются один от другого по подготовительным операциям, которые должны быть предусмотрены в алгоритме и ясны из формальной модели. Последнее и заставляет присваивать различным ситуациям разные символы управляющих функций Ф^,; ( = 1, 2). Любое явление может либо присутствовать в рассмотрении, либо отсутствовать. Наконец, присутствие явления может быть неполным. Изложенное охватывает все такие случаи в отношении функций Ду.

Алгоритм, реализующий приведенную формальную модель, является существенной частью общего процесса решения задачи на определение координат точек, принадлежащих линии пересечения поверхностей второго порядка. Исходной для рассматривае-. мого алгоритма является пара уравнений поверхностей, а также поле задачи, заданное в виде неравенств. Исходным является и некоторый стандартный шаг параметра б. Задается также число е, характеризующее точность приближения корней. Для ускорения решения можно на каждом шаге z = hix заново ограничивать поле решения, учитывая расположение точек, принадлежащих линии пересечения в плоскости z = h. Пусть, например, на шаге 2 = hi получились точки, принадлежащие искомой линии пересечения и имеющие координаты (Xi, hjy ; /i,); к^ (х^, hj.; hi). Имея в виду регулярность исходных поверхностей, их порядок и небольшую величину шага б= Я,+1 - Я,-1, можно осуществить сужение поля задачи, приняв, например, для шага = hii следующие границы: = Яу+ - 26,-.2; /in,ax!=

= hj+n + 26j+2 - в окрестности корня и hi = /ly+m -

- 26j+2; /W = /i/+m + 26,+2 - в окрестности корня k. При дальнейшем решении задачи сужение поля задачи происходит алгоритмически по этим формулам. В случае, когда корни и 2 близки друг другу, можно наименьшую по значению координату, изменяемую при поиске, принять для определения по приведенным формулам, а наибольшую координату использовать для нахождения /imax- В первом из обсуждаемых случаев поле задачи будет расчленено на части, образующие окрестно-ети участков искомой линии пересечения. Во втором случае отдельные части полей соединяются, стягиваясь к области возможного расположения корней.

Изложенный процесс корректирования границ поля задачи на каждом шаге моделирует использование прошлого опыта. Как известно, деятельность человека в игровой системе управления может быть условно разбита на следующие этапы:

а) информационный поиск, включая ознакомление с обстановкой, ее оценку и выделение тех элементов, по которым необходимо принять решение;

б) принятие ;?ешения на основе анализа выделенных элементов;

в) передача информации о принятом решении или осуществление управляющих воздействий.

В приведенной формальной модели содержится попытка в известной мере моделировать эту деятельность.

Более подробно моделирование деятельности человеках целью ее автоматизации на базе ЭВМ рассмотрено в следующих главах.

Глава IV. ЭВРИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕШЕНИЯ ЗАДАЧ

Для того чтобы прийти к машинным алгоритмам, обеспечивающим построение и использование чертела с помощью ЭВМ, необходимо построить формальные модели процессов получения и чтения чертежа человеком.

I. ОСНОВНЫЕ ПОЛОЖЕНИЯ

В дальнейшем будем называть совокупность действий, направленных на решение задач, возникающих в процессах чтения и построения чертежа, графическим конструированием (ГК). Для решения проблемы автоматизации инженерной графики необходимо создать формальную модель ГК. Рассмотрим типы задач, возникающих в ГК с точки зрения проблемы формализации. Все эти задачи можно условно разделить следующим образом:

а) задачи, сводимые к формулам, моделирующим известный геометрический алгоритм;

б) задачи, алгоритм решения которых не известен, но разрешаемые человеком на основе опыта и интуиции;

в) задачи, которые вообще нельзя разрешить алгоритмически по тем или иным причинам (слабость оборудования, принципиальная алгоритмическая неразрешимость и т. п.).

Задачи типа а условно назовем формальными, типа б - неформальными, тип в будем характеризовать термином нефор-мализуемые . Одни и те же в содержательном смысле задачи могут переходить из одного типа в другой. Так, расширение вариантности исходных данных приводит к увеличению массовости алгоритма. Но при этом задача типа а может перейти в тип б или даже в тип в. Примером задачи типа а являются рассмотренные выше позиционные и метрические задачи на чертеже, связанные с простейшими геометрическими образами. Задача определения видимости линий на чертеже является формальной, так как имеет известный

алгоритм. Иногда эта задача переходит в неформальную из-за большого разнообразия пространственных структур, которые могут быть образованы проецируемыми фигурами. Неформальными задачами (хотя и регламентируемыми ЕСКД) является выбор видов комплексного чертежа, положения и числа секущих плоскостей при организации на чертежах сечений и разрезов, масштаба и формата чертежа, размещения и нанесения на чертеже размерной информации.

С нашей точки зрения исследование и разработка алгоритмических решений неформальных задач является той основой, на которой может быть построена автоматизированная система инженерного черчения. Прежде всего возникает проблема постановки неформальной задачи, если неизвестен алгоритм, а часто и метод ее решения. Возьмем. задачу чтения чертежа. Даже сам термин чтение чертежа истолковывается специалистами по-разному. Часто вообще избегают пояснять этот процесс, полагая, что всем он интуитивно ясен и может быть пояснен примерами. Такой подход к определению встречается часто, является достаточно привычным й не вызывает затруднений до тех пор, пока не возникает необходимости в автоматизации процесса решения подобной задачи. Дело в том, что математическая постановка такой задачи затруднительна либо невозможна при том уровне информированности о ее решении, который имеется.

Нечеткости формулировок, различные неоднозначности вырастают в непреодолимые преграды при попытках создать алгоритм решения. Появляется проблема установления жестких ограничений, уточнения определений, классификации случаев и т. п. Все это является предварительным этапом процесса, в ходе которого закладываются основы для алгоритмического решения поставленной задачи.

Первым этапом построения формальной модели неформальной задачи является изучение поведения человека в ходе решения. Это поведение отображается затем в виде связного описания. Будем называть процесс описания поведения человека в ходе решения неформальной задачи эвристическим моделированием. Как будет показано, последнее ведет к более или менее четкой постановке неформальной. задачи: четко выявляются исходные данные и наложенные на них ограничения, определяются признаки правильности решения и т. д. Рассмотрим более подробно метод эвристического моделирования.

2. СОВРЕМЕННОЕ СОСТОЯНИЕ ВОПРОСА

При эвристическом моделировании происходит процесс создания модели в виде описания либо схемы цепи действий, которые производятся мысленно и отражаются в поведении человека при решении неформальной задачи. Попытки моделировать деятельность мозга предпринимаются давно. Исследования работы мозга

восходят к и. М. Сеченову и И. П. Павлову. В 1935 г. Н. А. Берн-штейн выдвинул идею о том, что в основе сложных форм работы мозга лежат программы различного уровня. Появление ЭВМ придало этим исследованиям некоторый новый смысл: создать искусственный разум, искусственный интеллект, используя для этого достижения математической логики, кибернетики, электроники. На этом пути возникают различные подходы. Для целей кибернетики наиболее плодотворным оказался информационный подход. Его сущностью является последовательное применение к моделированию работы мозга принципа, черного ящика . Моделирование при этом происходит на уровне информационных процессов, которые могут быть восприняты и интерпретированы ЭВМ. Процесс рассматривается вне зависимости от физической структуры, перерабатывающей информацию. Элементарной единицей, рассматриваемой в этом подходе, является информационный процесс типа: запись сигнала в памяти, стирание сигнала, сравнение двух сигналов и т. п. Такое расчленение сложных сигналов и процессов переработки информации на элементарные было положено в основу эвристического программирования. Авторами одних из первых эвристических программ были А. Ньюэлл, К. Саймон, Д. Шоу. В последующем были созданы другие эвристические программы: для игры в шашки, шахматы, для доказательства геометрических теорем, балансирования работы сборочного конвейера.

Особенностью эвристических программ является то, что поиск начинается в условиях, когда неизвестен алгоритм и отсутствует информация о возможности решения. Стратегия поиска, который осуществляется специальной программой, изменяется в зависимости от тех или иных пробных действий. Таким образом, применяется тактика проб и ошибок с использованием специальных приемов, позволяющих сократить поиск. Эти приемы или правила называются . эвристики . Программа, построенная на эвристических принципах, не гарантирует полного успеха во всех теоретически мыслимых ситуациях, однако в большинстве встречающихся случаев приводит к успешному решению. Этим эвристический алгоритм отличается от обычного.

Установленных понятий и принципов науки об эвристическом программировании пока не существует. Как заявил В. Рейт-ман на XVni Международном психологическом конгрессе (Москва, 1966 г.), эта наука переживает период своего средневековья. Слово эвристика употребляется в различных смыслах: как обозначение действия или правила, ведущего к цели; как обозначение отрасли науки (особенно в отечественной литературе последних лет). Эвристические программы весьма сложны и дороги, они плохо справляются с изменениями ситуации. В последние годы на основе критического анализа к первоначальным вариантам эвристического программирования начали добавляться новые, основанные на более глубоком моделировании мышления приемы.

Основной трудностью эвристического программирования и его