Это описывающая функция идеального реле. На рис- 2.4-4 изображена величина

N{B)

в зависимости от отношения h/B. При /г=0 можно использовать тот же график с h вместо k.

Реле с зоной нечувствительности ( мертвой зоной) и гистерезисом. Описывающая функция трехпозиционного реле с зоной нечувствительности и гистерезисом равна

B>d,

Т = - 4 arcsin (4 ) ~ sin (-) . (2.4-6)

Отметим, что подстановка rf=-е приводит к комплексной описывающей функции двухпозиционного реле с гистерезисом, которая приведена выше. Кроме того, если d=e=0, вновь получается действительная описывающая функция идеального двухпозиционного реле. Наконец, d=e дает действительную описывающую функцию трехпозиционного реле с зоной нечувстви-тельносги:

А^() = 44/М47- (2.4-7)

Описывающую функцию трехпозиционного реле с зоной нечувствительности и гистерезисом можно определить из кривых на рис. 2.4-5 По оси ординат откладывается величина

Параметрами кривых являются

d + е~ а

По оси абсцисс откладывается величина

е + d а .а

Случай hla=Q соответствует трехпозиционному реле без гистерезиса. При этом, так как e=d, абсциссой является величина diB.

Гистерезис, или петля. Описывающая функция рассмотрена в примере 2 разд. 2.2. Графики ее нормализованной абсолютной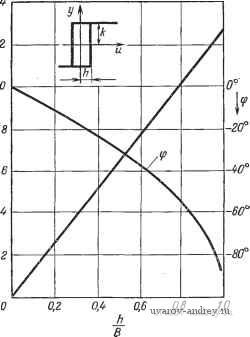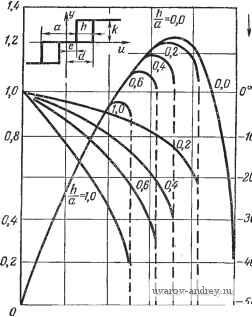

0,6

Рис, 2.4-4. Описывающая функция двухпозиционного реле с гистерезисом.

0,Z 0,4 0,6 0,8 Ifi 2В

Рис. 2.4-5. Описывающая функция трехпозиционного реле с зоной нечувствительности и гастерезисом.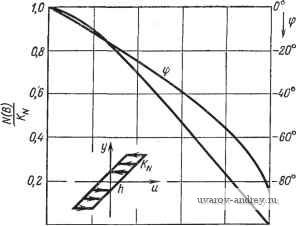

о 0,2 OA 0,6 0,8 1,0

т

Рис. 2.4-6. Описывающая функция нелинейности типа гистерезиса (петли).

-10° -20°

-30°

О о,г о,и 0.6 0,8 W в

Рис. 2.4-7. Описывающая функция составного отрицательного дефекта.

величины и фазового угла в зависимости от hIB приведены на рис- 2.4-6. Чем больше амплитуда входного сигнала, тем лучи1е абсолютная величина описывающей функции аппроксимирует коэффициент усиления Kn.

Отрицательный дефект. Описывающая функция

.Н8А/,-(1)Ч1б(А)/, ,2.4.8)

является комплексной величиной с фазовым углом Ф = arctg-г

Графики нормализованной абсолютной величины и фазового угла в зависимости от относительной величины Ь/В приведены на рис. 2.4-7.

2.5. ПРИБЛИЖЕННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ОПИСЫВАЮЩИХ ФУНКЦИИ

Цыпкин [26] предложил следующий метод для определения описывающих функций.

Для однозначной симметричной нелинейности Ai = 0 и

Б, = 1- J g (5 sin сог!) sin (В/ diut (2.5-1)

о

Коэффициент Bi можно также определить в виде

Б, = 4 J g (В sin (ut) sin Ы dwt, (2.5-2)

-t.I2

так как gf -нечетная функция. Возьмем и в качестве новой переменной. Тогда

и = Bsin wt, du = В cos (ut dmt, (2.5-3)

cos mt= ± l/1 - {a/B)\

где знак плюс берется в первом и четвертом квадрантах, а минус- во втором и третьем. Следовательно,

2 LimMdiulB). (2.5-4)

Этот интеграл можно вычислить по формуле Стеклова 127]

i- J - dx = 11/(1) + 2/(0,5) + 2/(-0,5) +/(-1)] + т,

(2.5-5)

где остаточный член равен

т = -

2=6!

(- К S < 1).

(2.5-G)

Заменяя х на и\В и /(х) на g(u){u/B) и отбрасывая остаточный член, получим приближенное выражение для описывающей функции

N(B) \g{B) + g{B/2)].

(2.5-7)

Эта формула тем точнее, чем меньше остаточный член. Так как остаточный член содержит производную шестого порядка,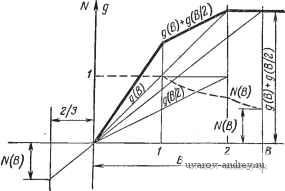

Рис. 2.5-1. Описывающая функция нелинейности типа насыщения, определенная методом Цыпкина.

формула дает точные результаты для полиномов до пятого порядка включительно.

Если требуется более высокая точность, можно использовать формулу

[giB) + giB/2) + Vbg{y~3B/2)], (2.5-8)

N{B)

которая дает точный результат для полиномов до одиннадцатого порядка.

с помощью более простого уравнения (2.5-7) значения описывающей функции можно определить из пропорции

N{B): 2/3 = \g {В) + g {В/2)\: В. (2.5-9)

На рис. 2.5-1 представлена таким образом описывающая функция нелинейности типа- насыщения.

Уравнение (2.5-7) можно использовать также для решения обратной задачи определения нелинейности g(u), связанной с данной описывающей функцией N(B). Если амплитуда входного сигнала принимает значения В, В/2, В/4, В/2 , то

N(B)g(B)+g{B/2), -N{B/2)-g{BI2)-gm), + NiB/2) = (5/22) + g{BI2)

(-1) - /V(B/2 ) = (-l) g(B/2 ) + (-l) g(B/2 +i).

Произведя суммирование и отбрасывая член (-l) g (B/2 +), получаем

g{B) = 2 (-1) W- т )- (2.5-10)

Обычно достаточно ограничиться несколькими первыми членами.

Метод Цыпкина аппроксимации описывающих функций можно распространить на многозначные (обычно двузначные) и несимметричные нелинейности. В этом случае интегрирование выполняется по углу на отрезке длиной 2я (для получения среднего значения необходимо разделить на удвоенный угол). Для применения формулы Стеклова интегрирование по частям от я/2 до Зя/2 сводится к интегрированию от -я/2 до я/2 с учетом, чго косинус отрицателен во втором и третьем квадрантах и положителен в первом и четвертом.

Пусть

, , , gi( ). если и>0, ,оп ч

g(u) = 1 , . r (2.5-11)

g2 (и), если и < 0.

U,(tt), если и>0, ,оп ч

g(u) = 1 , . r (2.5-11)

\ g2 (и), если и < 0.

В формуле Стеклова f{x) следует заменить соответственно xgii, VgiiB) и giixB), (/ = 1, 2). Сучетом знака

получим

,( , н), и>0.

q{B) = = -[gm+gim)-gi(-B/2)~g,(-B)],

(2.5-12)

g(B) = = [g, (6/2) + g, {-B/2)~g2 {BI2)~g, (-6/2)1,

(2.5-13)

0= 2 f() + gim)+2g,{-BI2)+g,{-B)\.

(2.5-14)

Кроме того, данный метод можно применять для выражений, содержащих постоянную составляющею V:

к (О = f/ -f 5 sin 0), (2.5-15)

а также несимметричных однозначных и многозначных нелинейностей

g{-u)фg{ti). (2.5-16)

Ограничиваясь однозначными несимметричными нелинейно-стями, получим, что 1(х) надо заменить на

xgiU + хВ), \/\-xg{U + хВ) и g {U + хВ) соответственно:

д(В, U) = [g{U + B)+g{u +-f) -g [и -4) g(f/ 5)l,

(2.5-17)

g(,B, f/) = 0, (2.5-18)

9 (Д U) =\g{U + B) + 2g{u + 1) 4-2g(U-§-)+giU-B)].

(2.5-19)

Аналогично можно рассмотреть двузначные нелинейности, определенные уравнением (2.5-11). В этом случае можно использовать уравнения (2.5-12)-(2.5-14), заменив ±В на U±В, ±В/2 на и±В/2 и положив gOAJU.

Наконец, если работа нелинейного элемента описывается дифференциальным уравнением

у=/{и,й), (2.5-20)

где

xf{xB, ±шВ]/1-л2), V\-xf{xB, ±шВ1Л-х2)

f{xB, +шВУТ) соответственно надо подставить в формулу Стеклова. Отсюда

(-1Г' в¥)-Л-а,о)]. (2-S-21)

-4h -вЩ-Л

В г, V 3

(2.5-22)

+ 2/,(-B, {-iy-шВ) +/Л-В, 0)]. (2.5-23)

Аналогичные, но несколько более сложные соотношения можно написать для входного сигнала вида u(t) = U+B smait.

Пример 1. Уравнение нелинейного элемента

и, к > О,

( к, к > О,

является несимметричной однозначной функцией. Из уравнений (2.5-12) -(2.5-14) находим

9(Б) = . д'{В)0, Ао = 4. Кроме того, ряд Фурье для выходной переменной имеет вид y{t) = В --\-~5тЫ - cos2(1)/ -Ь ...j-

Таким образом, в данном примере СВ) и 9(В) можно точно определить, используя приближенные формулы. В то же время для Ао получается В/3 вместо точного значения В/п.

Пример 2. Линеаризуем преобразователь, заданный дифференциальным уравнением

X = и - е(1-и^) й.

По формулам (2,5-21) - (2.5-23) получаем д'{В, ш) = -га)(1-

Ао(В, ш) = 0.

Результаты полностью согласуются с теми, которые были получены в примере 3, разд. 2.3 при условии, если сделать поправку на несколько различные постановки обеих задач.

2.6. другой приближенный метод для определения описывающих функций

Дуке [28] предложил другой приближенный метод для определения описывающих функций. Начнем опять с выражения

где знак плюс берется в первом и четвертом квадрантах [d{ulB)>0], а минус во втором и третьем [с?(и/6)<0]. Так как

dl-( /6)2 = -m=d( /6).

iujB)

и у i-yuiD)- = -

В,-+~ lg{u)d}/\-{u/Bf. (2.6-2)

Введем новую переменную интегрирования v:

v==V\~(ulBf.

Обозначим функцию g{u) через gi, если и>0, ы>0, через g, если к > О, н < О, через gg, если < О, н < О, и через gi, если и<0, ы>0 (рис. 2.6-1). Тогда

р о 1 о 1

-[gidv+gdv-Srgdv - gdv

1 0 1 о

a = i т. е.

А = V J + 2 ~ 3 - &) dv. (2.6-3)

Для нечетной функции g{u) g3=-gi и gi=-g2. Следовательно,

Bx=-l{gi+g2)dv, (2.6-4)

тогда как для однозначной функции

Bx-~yg,-gs)dv. (2.6-5)

Наконец, для однозначной нечетной функции

Bx-g,dv. (2.6-6)

Приближенные значения трех приведенных выше интегралов

Рис. 2.6-1. Интервалы интегрирования многозначной нелинейности.

можно получить, заменяя интеграл суммой. Например, в последнем случае

п

B,-\gMlV\-i}iim. (2.6-7)

Самый простой способ решения состоит в определении значений функции g{u) при значениях квадратного корня, которые берутся через равные промежутки. В табл. 2.6-1 приведены отношения и/В для десяти интервалов длиной 0,1 между О и 1

функции V -{tilBf.