зистационарное) состояние, показывают, как система колеблется вблизи минимума л;=0, v = 0. Период треугольного сигнала X равен 2Т; период сигнала v равен Т. Сигнал z описы-

Рис. 3.2-3. X, V, z -а и ъ зависимости от t д.та квазистациоиарного состояния оптимальной системы с поисковым процессом с самовозбуждающимися колебаниями.

вается пилообразной функцией, а и является прямоугольной волной. При квадратичной зависимости [выражение (3.1-4)] получаем

где ЛГ-максимальная амплитуда х, так как

йх 2Х

(3.2-2) (3.2-3)

Из выражения (3.2-2) находим пиковую амплитуду

Z = k, (3.2-4) так как из выражения (3.1-4)

1/= kX\ (3.2-5)

то, следовательно,

7 - д.

т

Z = 4-. (3.2-6)

Таким оЗразом, максимальное отклонение выходного сигнала V от будет равно

У-Щ-- (3.2-7)

Теоретически это отклонение может быть минимизировано без ограничений путем уменьшения пороговой величины Z. На практике, однако, величина Z не может быть сделана очень малой из-за шума дифференциатора D. Аналогично время Г нельзя сильно уменьшить, так как в этом случае шум от интегратора был бы значительным. Интегрируя dxldt=Uo/Ti от О до Г/2 (или из рис. 3.2-3), получаем

Uo Т

X-!f-\, (3.2-8)

откуда с помощью выражения (3.2-5) имеем

гяе К - Uq\/k/Tr - коэффициент усиления контура (обратно пропорционален периоду). Учитывая выражение (3.2-6), максимальное отклонение V можно записать в виде

У--- (3.2-10)

По соображениям, изложенным выше, эта величина не может быть сделана сколь угодно малой. Обычно используемой мерой ошибки служит среднее значение, а не само значение V:

7 7/2

y = Yl it)di-Yi ()- (3.2-11)

Так как в течение полупериода [см. выражения (3.1-4) и (3.2-3)]

/.14 /, / ЗА- Л2 , 4.Y2 ,

то, применяя соотношение (3.2-5), получим хорошо известный результат:

V= kfidt==kX==±V. (3.2-12)

о

Используя выражение (3.2-10), получаем

Vm = (3.2-13)

В этой адаптивной системе поисковый процесс и подстройка объекта (или системы) управления (т. е. основной процесс) объединены и происходят одновременно. Изменение входной переменной х и дифференцирование выходной v позволяют определить знак производной dvjdt и установить, приближается ли система к минимуму или удаляется от него.

Если при прочих равных условиях оптимальная система содержит также факторы, связанные с временными задержками, то даже если Z и Т останутся теми же, амплитуда V, а следовательно, и среднее значение Vm увеличатся. Допустим, что временные задержки Ti и Тг происходят на двух концах оптимизируемого объекта (системы) S (рис. 3.2-4). В этом случае входная переменная х' и выходная v всего объекта (или системы) будут отличаться от переменных х и v. Зависимости отдельных переменных от времени приведены на рис. 3.2-5. Сигнал х' прерывается, как только Z достигает заданной величины Z. После этого Z возрастает в течение времени Тт-Г1+Г2 до величины

где Z>Z. Уравнение (3.2-7) остается справедливым при подстановке Z вместо Z:

V-. (3.2-14)

Выражение (3.2-9) также остается справедливым. Из кривой z{t), на рис. 3.2-5 следует, что

( 1 + b)-TT=-Z- Z. (3.2-15)

Следовательно, принимая во внимание выражение (3.2-9), получим

Z = -4==-4. (3.2-16)

Т Yv

Новое выражение для среднего значения имеет вид

-=1(4- + )- (3.2-17)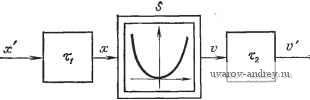

Рис. 3.2-4. Блок-схема объекта или системы, содержащая элементы с временными задержками.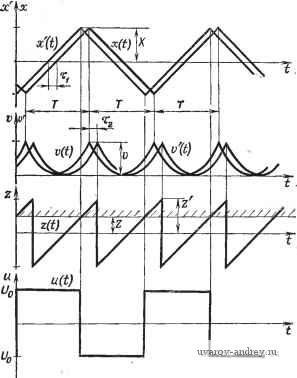

Рис. 3.2-5. х', V, Z и и в зависимости от t для квазистационарного состояния оптимальной системы с поисковым процессом с самовозбуждающимися колебаниями при наличии временных задержек.

При заданных значениях Z и К ъ результате временных задержек Тт получим большее среднее значение, чем при Тт = 0. Из уравнения (3.2-17) следует, что слишком малые значения К столь же нежелательны, как и слишком большие. Простое вычисление экстремума приводит к следующему оптимальному значению коэффициента усиления контура:

о=/ -2. (3.2-18)

Утгшп = 4 (3-2-19)

При заданном времени Тт и отклонении Z среднее значение квазистационарных колебаний не может быть уменьшено за счет увеличения коэффициента усиления. Если в объекте или системе управления элементы с временными задержками заменены энергетическими емкостями или осциллирующими элементами второго порядка и выше, то вычисления значительно усложняются. Однако качественные выводы остаются теми же.

Оптимальные системы с вынужденными колебаниями. В других типах систем с непрерывным поисковым процессом для детектирования используется синусоидальная волна [7, 40*, 74*, 76*]. Этот процесс иногда называют синхронным детектированием. Блок-схема такой системы показана на рис. 3.2-6 (поисковый и основной процессы не идентичны, но одновременны и накладываются друг на друга). Входная переменная управляемого объекта или системы S состоит из двух компонент:

х = а-{- А sin шо, (3.2-20)

где А и сио - постоянные, а - входная переменная основного процесса и Asimocit - детектируемый сигнал, полученный с помощью генератора G. Предполагается, что амплитуда А мала и а изменяется незначительно в течение периода То=2п/а>о. Если й<0, рабочая точка М расположена на левой ветви параболы (рис. 3.2-7). Основная частота выходного сигнала равна соо, а его амплитуда отличается от амплитуды входного и его фаза сдвинута на 180°. Отсюда следует, что переменная а должна возрастать. Если й>0, выходной сигнал в рабочей точке N такой же, как и в предыдущем случае, но имеет нулевой сдвиг по фазе. Отсюда следует, что а должно уменьшаться. Наконец, если а=0, рабочая точка находится в начале координат О и частота колебаний равна 2о)о.

Сигнал частоты соо может быть выделен из выходного сигнала V с помощью ленточного фильтра F\ (рис. 3.2-6), который не пропускает постоянные или медленно меняющиеся сигналы.

П

A sin Wgt

Рис. 3.2-6. Блок-схема системы или объекта с поисковым процессом с вынужденными колебаниями.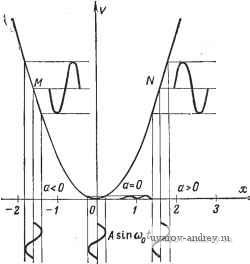

Рис. 3.2-7. Поисковые процессы оптимальной системы с вынужденными колебаниями.

Переменная составляющая сигнала подается на фазовый распределитель П, на выходе которого появляется составляющая постоянного тока, пропорциональная фазовому сдвигу входного переменного тока и дополнительного сигнала. Фазовый распределитель можно заменить умножителем П. Фазу дополнительного сигнала можно выбрать так, чтобы согласовать ее с фазой фильтра. Например, если ленточный фильтр заменить дифференциатором, выходная составляющая частоты о дифференциатора будет равна В cos соо^. В этом случае в дополнительном сигнале Л sin (соо^-Ьф) фазовый сдвиг должен равняться ф=л;/2, что приводит к А cos (Hot. Выходной сигнал умножителя Я в этом случае равен

= Л5со82шо= + -со82шоД (3.2-21)

Знак постоянного члена ABJ2 зависит от знака В: если В>0, то постоянный член положителен и выходная величина а интегратора с переменной знака будет уменьшаться; если же В<0, то эта величина будет возрастать. Влиянием составляющей переменного тока {АВ/2) cos2mt на интегратор в первом приближении можно пренебречь.

Исследуем систему более подробно. Прежде всего подставим выражение (3.2-20) для х в уравнение (3.1-2):

V = k{a + Asm %tf = k{cfi+ -\-2aA sin %t - у cos 2(В{,# ) .

(3.2-22)

Переменная составляющая частоты равна

г)ш„ = 2kaA sin wf. (3.2-23)

Можно считать, что выходной сигнал z фильтра F\ изменяется как производная 2шо аЛ cos (в переменной составляющей Иш,. Поэтому для выходного сигнала умножителя получаем следующее выражение:

и = С (- -Ишо 1 Л cos (Bfl = 2(Во аАС cos о/? =

= /(ВооЛ2СЧ-шоаЛ2Ссо8 2сво^. (3.2-24)

Дифференциальное уравнение интегратора имеет вид

=-1и=-~ Ы^АЮ - (во аАЮ cos2 Шо. (3.2-25)

Если частота соо достаточно велика, то составляющей частоты 2сйо на выходе интегратора можно пренебречь. Опуская эту составляющую в выражении (3.2-25), получим для а дифференци-

альное уравнение

Г^ + а = 0, (3.2-26) где постоянна/1 времени равна

Т--Лг- (3:2-27) Решение этого уравнения имеет вид

a{t) = a{0)e-tir, (3.2-28)

т. е. a(t) убывает экспоненциально. Отметим, что это решение справедливо только в первом приближении, так как составляющая частоты 2сйо была отброшена. Влияние этой составляющей можно уменьшить с помощью другого фильтра F2. Отметим также, что при замене производной от v на производную от v о в выражении (3.2-24) появляются составляющие частот соо и Зсоо. Однако ими также можно пренебречь в первом приближении.

В конце переходного процесса а становится равным нулю, хотя поисковый процесс будет продолжаться со средним значением

уш-к^. (3.2-29)

Из выражения (3.2-20) видно, что чем меньше Л, тем меньше У™. Однако уменьшение А увеличивает постоянную времени Т переходного процесса. Более хорошее решение состоит в том, чтобы подавать на умножитель П вместо сигналов В cos соо^ и А cos соо^ сигналы sign(BcoscuoO и sign (Л cos сооО. каждый из которых получается с помощью реле. Однако из-за наличия шума и зоны нечувствительности у реле величину Лив этом случае нельзя уменьшить по желанию.

Если имеется временная задержка, то дифференциальное уравнение (3.2-26) можно заменить в первом приближении следующим:

Т - G ( Гт-) = 0. (3.2-30)

В системе управления с жесткой обратной связью последнему уравнению соответствует передаточная функция

0{s)e-t. (3.2-31)

- = -S-. (3.2-32)

то с помощью диаграммы Найквиста легко доказать, что имеет место предельный цикл, т. е. система крайне демпфирована. При фазовой границе свыше 45° предполагается, что Т/Тт<л/4. Однако, если отношение Тт/Т превышает я/2, поисковый процесс становится неустойчивым. Поэтому необходимо увеличивать Т или вводить другие средства стабилизации (например, компенсаторы) .

Оптимальная система с памятью. Другим вариантом оптимальной системы является так называемая оптимальная система

м

BHhr

Рис. 3.2-8. Оптимальная система с памятью.

с памятью, в которой объединены основной и непрерывный поисковый процессы. Блок-схема такой системы приведена на рис. 3.2-8. Величина v изменяется с кусочно-постоянной скоростью. Статическая выходная характеристика v описывается параболой. Сигнал V поступает на за21оминающее устройство М, на выходе которого получаем v. Если v убывает, то v = v.

Однако, если v снова возрастает, то о поддерживается на последнем минимальном уровне. Так как допускается, что этот уровень является нулевым, будем иметь f = 0 на возрастающей ветви параболы (рис. 3.2-9). Запоминающее устройство Л1 можно реализовать несколькими способами [8-10, 25*, 74*, 76*, 78*]. Простое аналоговое устройство представлено на рис. 3.2-10. Благодаря диоду D напряжение на конденсаторе С может ста^ новиться только более положительным. Если сначала v и v равны, а затем v начинает уменьшаться, результирующий сиг-

нал на входе сумматора будет отрицательным, а сигнал на его выходе - положительным. Конденсатор С, первоначально заря-женньш отрицательно, будет перезаряжаться через диод D с рос-том ~v (и убыванием v) до тех пор, пока оба сигнала у и г' совпадут. Процесс продолжается, пока v не обратится в нуль.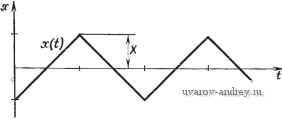

и

v(t),

Рис. 3.2-9. Процессы оптимальной системы с памятью.

а С ним вместе также и -f и v. Затем происходит возрастание V. Результирующий сигнал на входе сумматора становится положительным, а сигнад на его выходе -отрицательным. Диод D закрывается, и -v и г не меняются. Однако когда v начинает опять уменьшаться, электронный или механический переключатель К накоротко замыкается (с помощью не показанной здесь цепочки), конденсатор С заряжается отрицательно, диод