83*. 105*1:

nnis) = m s=>. (2.4-3)

Среднеквадратичная величина, появляющаяся на выходе блока ошибки слежения, обусловленной стохастическим шумом, может быть вычислена интегрированием спектральной плотности и выходного стохастического сигнала [30*, 83*, 105*]. Используя правило замены переменных, получаем

/оо /оо

) = 2Ь I*-()=2b I Wi-s)W{s)0 {s). (2.4-4)

-Jca -Joo

Используя выражения (2.2-1) и (2.4-3), находим

Вычисляя интеграл с помощью теоремы о вычетах, находим [29*. 105*1

Ш= . (2.4-6)

Уменьшение стохастической ошибки, следовательно, требует уменьшения w. Для удовлетворения противоречивмх требований возьмем в качестве критерия квадрат установившейся ошибки в скорости плюс среднеквадратичную ошибку, обусловленную шумом:

el(oo) + .T(7)=ifi + -. (2.4-7)

Минимум этого выражения достигается при частоте

да-- (2-4-8)

При заданном уровне шума и постоянном коэффициенте затухания собственная частота соо должна регулироваться как функция бортовой переменной. В обычной неадаптивной системе управления соо выбирается для некоторого типа средней скорости V, а при других входных значениях должны быть разрешены возрастающие ошибки. В адаптивную систему управления встроен дополнительный контур, V определяется по входному сигналу, момент инерции / постоянен, а коэффициенты усиления К и затухания D изменяются таким образом, что удовлетворяется равенство (2.4-8) и t поддерживается постоянным. Из соотношения (2.2-19) следует, что К должно изменяться как V\ а D как Г',.

2.5. АДАПТИВНЫЕ СИСТЕМЫ С ЭТАЛОННОЙ МОДЕЛЬЮ

В работах [6, 7] был предложен ряд адаптивных систем с эталонной моделью. Затем последовали несколько практических реализаций, одна из которых относится к области сверхзвуковой авиации [8].

Хотя обычно подчеркивают преимущества адаптивных систем с эталонной моделью, до сих пор нет обоснований предпочтительности одной адаптивной системы перед другой. Пока нет ни одной законченной теории систем с эталонной моделью. Именно поэтому нами рассматривается только несколько примеров.

В адаптивных системах с эталонной моделью основную роль играют модели. В системе, показанной на рис. 1.2-3, выход аналоговой модели удовлетворяет некоторому критерию качества. Адаптивная система управления сравнивает управляемую переменную с выходом модели, например с помощью преобразователя, и подстраивает параметры обычно управляющего устройства таким образом, чтобы минимизировать разность между двумя сигналами, т. е. минимизировать либо среднее, либо абсолютное отклонение.

Ниже рассмотрены методы подстройки параметров, возмущения параметров и приращения управляемой переменной.

Отметим, что ни один из методов не является универсальным. Каждый из методов имеет свои преимущества и недостатки, которые проявляются в приложениях. На практике должен быть достигнут компромисс между сложностью, реализуемостью и надежностью.

Методы подстройки параметров. Рассмотрим систему, блок-схема которой приведена на рис. 2.5-1. Входной эталонный элемент, управляющее устройство, датчик и преобразователь в цепи обратной связи и объект управления образуют обычную замкнутую систему управления. Адаптивная система реализуется с помощью эталонной модели и энергетического элемента. Модель может быть как аналоговой, так и цифровой. Разность между управляемой переменной и выходом модели дает ошибку. Сигнал ошибки подается на вход элемента мощности, который подстраивает параметры компенсатора на входе объекта управления или в цепи обратной связи, а также входного элемента до тех пор, пока сигнал ошибки не станет равным нулю. Дифференциальные уравнения замкнутой системы управления и модели обязательно одинаковы. Если данные с объекта управления подвергаются каким-либо изменениям, параметры управляющего устройства (т. е. компенсатора) должны изменяться аналогичным образом до тех пор, пока разность между выходами модели и системы не станет равной нулю. Адаптация может

быть осуществлена несколькими способами: с помощью построения пространства состояний из разностей между соответствующими параметрами модели и системы управления, а также из функционалов или функций от сигнала ошибки, к которым могут быть потом применены методы оптимизации (описываемые в разд. 2.3 данной части), и с помощью второго метода Ляпунова.

Эталонный элемент

Компенсатор Объект

6r(s)

c(t)

J Компенсатор в цепи обратной связи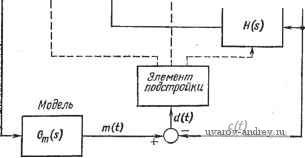

Рис. 2.5-1. Блок-схема адаптивной системы с подстройкой параметров.

Методы возмущения параметров. Принципы методов возмущения параметров [9-И] иллюстрируются на рис. 2.5-2. В этом случае действие эталонной модели отлично от действия, описанного выше. Сигнал разности d(t), который получается из выхода модели и управляемой переменной, используется для формирования функции вида

f{d) = d- или f{d)\d\, или f{d)\d\\ (2.5-1)

Один параметр системы задается в форме

а = о -f а„ -f 1 cos t,

где Оо - постоянная часть параметра, c - корректирующее изменение, выполняемое адаптивным элементом, Cicosco/ - синусоидальное возмущение, вызывающее непрерывное появление ошибки. Последняя подается также на адаптивный элемент. За счет возмущения появляется компонента частоты со в сигнале разности d. Величина и знак корректирующей переменной о должны быть выбраны так, чтобы уменьшить среднюю величину

функции ошибки f(d), подсчитываемую по короткому интервалу времени.

Можно построить также систему, управляющую более чем одним параметром. В этом случае каждому параметру должна быть предназначена своя возмущающая переменная определенной частоты и отдельный адаптивный контур. Было обнаружено [91*], что, если все коэффициенты усиления контуров равны, подстройка параметров будет происходить по траектории наискорейшего спуска. Для дальнейшего улучшения работы лучше всего добавить к адаптивной системе фильтр и некоторые нелинейные элементы.

r[t)

Модем

Элемент

Осциллятор я, cos cct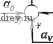

+ с, cos at

Рис. 2.5-2. Б.чок-схема адаптивной системы с возмущением параметров.

Недостаток метода состоит в том, что возмущение появляется также и в управляемой переменной. Это возмущение можно устранить только тогда, когда динамическая структура модели идентична или очень похожа на структуру объекта управления. В этих случаях возмущающим сигналом можно воздействовать на соответствующий параметр модели.

Методы возмущения могут быть реализованы и другими способами. Хотя адаптивный контур может выглядеть очень сложным, его конструкция на самом деле относительно проста.

Адаптивные системы с приращением возбуждающего сигнала. В третьем типе адаптивных систем с эталонной моделью проблема решается способом, отличным от метода возмущения параметров. Эталонная переменная r{t) подается как на модель,

так и на управляющее устройство. На вход последнего воздействует выходная переменная эталонной модели плюс управляемая переменная системы. Под действием этих переменных управляющее устройство выдает увеличенный сигнал возбуждения, который поступает на объект управления. Задача адаптивного управляющего устройства состоит в том, чтобы произвести возбуждающий сигнал, координирующий управляемую переменную системы и выход модели.

Основными проблемами являются выбор правильной эталонной модели и реализация адаптивного управляющего устройства.

ЛИТЕРАТУРА

1. Lang G.. Ham J. М. Conditional Feedback Systems, Trans. AIEE, 1955. 74, Pt. II.

2. Prince L. Т., Hendrick R. C, Lindahl J. H. Honneywells Flight Control System, Symposium on Adaptive Control, 1960.

3. Caldwell E. G. Applications of Adaptive Systems, Norair Report, 1961.

4. Anderson G. W., Buland R. N.. Cooper G. R. Use of Crosscolleration in an Adaptive Control System, Proc. Natl. Electron. Conf., 1959.

5. Simons J. C, Wayraeyer W. K. Adaptive Autopilot Study for a High Performance Interceptor Missile. Douglas Aircraft Company Eng., Paper 1026, pp. 88-94.

6. Масчов E. П., Осовский Л. М. Самонастраивающиеся системы с моделью (обзор). Автоматика и телемеханика, 1966, 27, № 6.

7. Земляков С. Д., Рутковский В. Ю. Обобщенные алгоритмы адаптации одного класса беспоисковых самонастраивающихся систем с модачью, Автоматика и телемеханика, 1967, 28, № б, стр. 88-94.

8. Whitaker Н. Р., Yarraon J., Kezer А. Design of Model Reference Adaptive Control Systems for Aircraft, MIT Instrumentation Laboratory Report R-164, 1958.

9. McGrath R. J., Rideout V. C. A Simulator Study of a Two-parameter Adap-five System. IRE Trans. Autom. Control, 1961. AC-6.

10. McGrath R. J., Rajararaan V., Rideout V. C. A Parameter Perturbation Adaptive Control System. IRE Trans. Autom. Control, 1961, AC-6.

11. Donalson D. D., Kishi F. H. Review of Adaptive Control System Theories and Techniques, в книге Leondes С. Т. (ed.) Modern Control Systems Theory, McGraw-Hill, N. Y.. 1965.

12. Pearson A. E. On Adaptive Optimal Control of Nonlinear Processes, Trans. ASME, 1964. 86, pp. 151-159.

13. Dressier R. M. An Approach to Modal-Referenced Adaptive Control Systems, IEEE Trans. Autom. Control. 1967, AC-12, № 1. pp. 75-80.

14. Shackcloth B. Design of Model Reference Control Systems Using a Lyapunov Synthesis Technique, Proc. lEE, 1967. 114, № 2. pp. 299-302.

15. Winsor Ch. A., Roy R. J. Design of Model Reference Adaptive Control Systems by Liapunovs Second Method, IEEE Trans. Autom. Control, 1968, AC-13, № 2, p. 204.

16. Landau I. D. A Hyperstability Criterion for Model Reference Adaptive Control Systems, IEEE Trans. Autom. Control, 1969, AC-14, pp. 552-555.

17. Porter В., Tatnall M. L. Performance Characteristics of Muti-variable Model-Reference Adaptive Systems Synthesized by Liapunovs Direct Method, Int. J. Control. 1969, 10, pp. 241-257.

18. James D. J. G. Stability Analysis of a Model Reference Adaptive Control System with Sinusoidal Inputs. M. J. Control. 1969. 9, pp. 311-321.

19. Sandoz D. J.. Swanick B. H. Real-Time Hybrid Simulation of an Adaptive-Control Technique, Proc. IEEE, 1970. 117, pp. 2165-2173,

3. МЕТОДЫ ОПТИМИЗАЦИИ

Операционные принципы автоматических оптимальных и экстремальных систем существенно отличаются от принципов, используемых в обычных автоматических системах управления. В оптимальных системах желаемая величина управляемой переменной v(t) заранее неизвестна. Следовательно, состояние системы необходимо анализировать в каждый момент времени для обеспечения системы информацией, необходимой для выполнения дальнейших оптимизирующих шагов.

Vr.V, -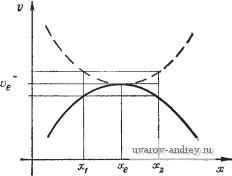

Рис. 3.1-1. Два варианта нелинейной характеристики v(x). Сплошная линия - максимум V, штриховая линия - минимум v.

Допустим, что некоторую переменную v требуется поддерживать на максимальном уровне. Переменная v является некоторой нелинейной функцией другой переменной х, т. е. v=v(x) (рис. 3.1.-1). При этом недостаточно знать какое-либо значение Vi, так как оно само по себе не дает направления, в котором должно изменяться х для достижения экстремума v=Ve. В состоянии v=Vi имеем x=Xi<Xe, в то время как при v=V2{ = vi) имеем х^Х2>Хе. Таким образом, начиная с x=Xi, х должно возрастать, а начиная с л:=Х2- убывать. Для выбора направления движения системы необходимо знать некоторые значения v в соседних точках кривой v(x). Для этого систему немного возмущают так, чтобы изменить величину х. Это равнозначно осуществлению поисковых (отладочных или тестовых) шагов. Автоматическое сканирование и поиск являются одним из основных процессов в оптимальных системах управления. Очевидно,

если зависимость v(x) известна заранее, максимум может быть достигнут с помощью простой программы управления. Тем не менее даже в этом случае оптимальное управление имеет преимущество, так как система может постоянно подвергаться действию возмущений, влияющих на ее точки максимума. Поисковые методы необходимьГ тогда, когда функция v(x) неизвестна заранее или сильно меняется под воздействием внешних возмущений. На основе информации, полученной в процессе поиска, система делает шаги для того, чтобы достичь заранее определенного состояния. Это называется основным процессом системы. Таким образом, в оптимальных системах различают два процесса: поисковый и основной.

3.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ

В автоматических оптимальных (экстремальных) системах поиск оптимальных операций объекта управления, экстремума некоторой функции одной или нескольких переменных, т. е. минимума функции затрат или максимума функции эффективности, делается автоматически [40*, 74*, 76*]. Автоматические системы управления включают объект управления (возможно, как элемент замкнутой системы управления) и специфическое устройство управления - оптимизатор, представляющее собой автоматическую аппаратуру, предназначенную для поиска оптимума и поддержания управляемого объекта на оптимальном уровне. Автоматический поиск означает изменение состояния системы, анализ влияния этого изменения и выбор шагов для достижения оптимума.

Под экстремальной характеристикой подразумевается функционал или функция стоимости (или эффективности) от скалярных переменных х и v или в более общем виде от векторных переменных х и v:

Q=Q(x, V). (3.1-1)

Предполагается, что функционал или функция Q имеет только один экстремум: максимум или минимум. Векторная переменная X называется входным вектором, а переменная v - выходным вектором. В некоторых случаях имеется только одна выходная переменная, и тогда и -скаляр. Вместо поиска экстремума при неявной зависимости Q(x, v) часто определяют экстремум при явной зависимости, когда

v = v(x). (3.1-2)

Функция v=v(x) в общем случае нелинейна.

Положение экстремальной точки подвергается возмущениям, воздействующим на объект. Величина v, соответствующая про-

извольному вектору х, называется рабочей точкой экстремальной характеристики. Обычно выполняют преобразование коор-динат, которое сдвигает экстремум характеристики v(x) в начало координат. При поиске максимума скалярная функция, или кривая v(x), часто аппроксимируется параболой

v-kx, k = const > О, (3.1-3)

а при поиске минимума-параболой

-v = kx, k = const > О (3.1-4)

при условии VgQ, Xe=Q, что может быть всегда достигнуто с помощью соответствующего преобразования координат.

Экстремальные системы обычно классифицируют по поисковому процессу, методам анализа и типу поиска.

Поисковые процессы. 1. Основной и поисковый процессы совпадают. В этих случаях в системе имеет место тенденция к возникновению самопроизвольных колебаний.

2. Основной и поисковый процессы осуществляются параллельно. В этом случае в экстремальной системе возбуждаются вынужденные колебания.

3. Поисковый и основной процессы происходят последовательно.

Методы анализа. 1. Система реагирует на производную dvjdx.

2. Система чувствительна к отклонениям переменной v. Тип поиска. 1. Поисковый процесс непрерывный. 2. Поисковый процесс дискретный, периодический или случайный.

Если требуется достичь максимума и рабочая точка лежит на правой ветви экстремальной характеристики, то dv/dx>0 является необходимым (хотя и не достаточным) условием для движения к максимуму. Если же рабочая точка лежит на левой ветви, то dv/dx<0, т. е. приближение к максимуму в этом случае должно происходить с отрицательной производной. Аналогичное рассмотрение можно провести для случая поиска минимума. Монотонный сдвиг по направлению к экстремуму иногда называют стационарной устойчивостью. Необходимое и достаточное условия стационарной устойчивости при поиске максимума состоят в следующем: если dx/dt>0, то dvjdtyO для того, чтобы удовлетворить условию dv/dx>0, в то время как если dx/dt<0, то dvldt>0 опять необходимо (и достаточно) для того, чтобы dvldx<0. Аналогично при поиске минимума если dx/dt>0, то dvldt<0 необходимо и достаточно для того, чтобы обеспечить dvldx<0, в то время как если dxldt<0, то dvldt<0 обеспечит выполнение условия dv/dx>0.

3.2. НЕКОТОРЫЕ ТИПЫ ОПТИМАЛЬНЫХ СИСТЕМ

Рассмотрим лишь некоторые типы экстремальных систем [1-5, 40*].

Оптимальная система, чувствительная к производной. На рис. 3.2-1 приведена блок-схема экстремальной (оптимальной) системы, чувствительной к производной. Эта система воспринимает производную dvldx после деления производной dvjdt на производную dx/dt, которые получаются на входе и выходе объекта управления или всей системы Р с помощью дифференциаторов D. Логический элемент L определяет знак производной, а с усилителя А и переключателя S снимается положительный или отрицательный сигнал Uo. Наконец, интегратор / является возбуждающим элементом. В этой системе имеется предельный цикл около рабочей точки в экстремуме. Недостатком данной системы, как, впрочем, и любой другой системы, содержащей дифференциатор, является ее чувствительность к шуму.

Оптимальная система с самовозбуждением. На рис. 3.2-2 приведена блок-схема системы, в которой реализован другой непрерывный поисковый процесс. Управляемый процесс или система (т. е. объект или система Р управления) имеет вход х и выход V. Пусть нелинейная зависимость v(x) описывается выражением (3.1-4). Предположим, что возбуждающий элемент / типа интегратора имеет передаточную функцию l/sTi. Оптимизатор О, отмеченный на схеме штриховой линией, может быть реализован различными способами. Одна из таких реализаций показана на рис. 3.2-2. Для анализа переменной v требуется прежде всего дифференциатор D. До тех пор пока производная z=dv/dt меньше, чем заранее определенная величина Z, на входе усилителя А с коэффициентом усиления KaI будет сигнал с отрицательным знаком. Выходной сигнал усилителя

w = Kj{z-Z) (3.2-1)

также будет отрицательным. Если z превышает Z, переменная W может принимать большие положительные значения, так как Ка>\, и триггер Ti изменит свое состояние. Импульс переключит триггерную цепь Гг (когда переменная w станет опять отрицательной, только первый триггер возвратится в исходное состояние, так как второй триггер чувствителен лишь к импульсам одного знака, например положительным). Выход и триггер-ной цепи Т, состоящей из элементов Ti и Гг, может принимать значения ±Uo. Соответственно х будет меняться со скоростью либо dx/dt= и о/Т i, либо dx/dt=-Uo/Tr. (Триггер Гг должен быть защищен от ошибочных импульсов, так как любой такой импульс вывел бы систему из окрестности экстремальной точки.) Кривые на рис. 3.2-3, описывающие стационарное (точнее, ква-

dx/dt

dv/dt R

Рис. 3.2-1. Б.чок-схема оптима.чьной системы, чувствительной к производным.

о

о

-О

г

и

Рис. 3.2-2. Оптимальная система с поисковым процессом с самовозбуждаюши-мися колебаниями. Внизу: подробная схема триггерной цепи.