Бисимость свойств передачи теплоты от скорости потока жидкости, обтекающего измеритель температуры в системе управления температурой, и зависимость от плотности воздуха, обтекающего управляющие рули ракеты.

1.6. АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ

В теории управления нелинейные системы анализируются обычно методами линеаризации, описывающих функций, статистической линеаризации, фазовыми методами и методами кусочной линеаризации. Некоторые задачи решаются численными и графическими методами.

Для решения нелинейных дифференциальных уравнений применяются методы аппроксимации, так как получить решение в замкнутом виде редко оказывается возможным. Наиболее широко распространенным и успешно применяемым методом является пошаговое интегрирование. Однако эта процедура требует довольно много времени (хотя цифровые вычислительные машины значительно сокращают объем вычислительных работ), и поэтому она не используется для установления общих зависимостей.

Графические методы связаны главным образом с фазовыми методами и их разновидностями, хотя имеются некоторые графические методы, соответствующие некоторым численным пошаговым процедурам.

ЛИТЕРАТУРА

1. Bennet W. R. А General Review of Linear Varying Parameter and Nonlinear Circuit Analysis. Proc. IRE, 1950, 38, pp. 259-263.

2. Bellin A. Non-autonomous Systems, Advance in Applied Mechanics. Academic Press, N. Y., 1953. pp. 295-320.

3. Karman T. The Engineer Grapples with Nonlinear Problems, Bull. Am, Math. Soc, 1940, 46, pp. 615-683.

4. Kalman R. E. Mathematical Description of Linear Dynamical Systems, SIAM J. Controls. 1963, 1. № 2, pp. 152-192.

o. Kalman R. E., Bertram J. E. General Synthesis Procedure for Computer Control of Single and Multi-loop Linear Systems, Trans. AIEE, 1958, 77, Pt. II, pp. 602-609.

b. Kalman R. E. On the General Theory of Control Systems, Proc. First Intern. Congr. Autom, Control, Moscow, 1960, v. 1, pp. 481-493; Butter-worth, London, 1961.

Kalman R. E. Canonical Structure of Linear Dynamical Systems, Proc. Natl. Acad. Set., 1962, 48, № 4, pp. 596-600.

Clauser F. N. The Behavior of Nonlinear Systems, J. Aeron. Set.. 1956. 23, pp. 41134.

- -чПе J. C, Wegrzyn S., Paquet J. G. Oscillation Sous-harmoniques dans n Asservissement par PIus-ou-Moins, Automatic and Remote Control, in , erworlh, 1964. V. I, pp. 204-209.

Ludeke C. A. The Generation and Extinction of Subharmonics, Proc. Symp, Nonlinear Circuit Analysis, v. II. Polytechnic Inst, of Brooklin. N. Y., 1953.

11 West J. С, Douce J. T. The Mechanism of Subharmonic Generation in a Feedback System. Proc. lEE. 1955. 102 (B), pp. 569-574.

12. Жилль Ж. К., Паке Ж. Ж. Субгармонические колебания в системах управления. Труды I конгресса ИФАК, Москва, 1960.

13. Cherry Е. С, Millar W. Some New Concepts and Theorems Concerning Nonlinear Systems, в книге Tustin A. Automatic and Manual Contro, Butterworth, Scientific Publications. London, 1952, pp. 262-274.

14. Caldwell R. R., Rideout V. C. Differential-Analyzer Study of Certain Non-linearly Damped Servomechanisms. Trans. AIEE. 1953, 72, Pt. II, pp. 165- 169.

15. Tustin A. The Effects of Backlash and of Speed Dependent Friction on the Slability of Closed-Cycle Control Systems. J. lEE. 1947. 94, Pt. Ila, pp. 143-151.

16. Tustin A. A Method of Analysing the Effect of Certain Kinds of Nonline-arity in Closed-Cycle Control Systems. J. lEE, 1947, 94, Pt. Ila. pp. 152- 160.

17. Haas V. B. Coulomb Friction in Feedback Control Systems, Trans. AIEE 1953, 72, Pt. II, pp. 119-126.

18. Hatanaka M. The Frequency Responses and Jump-Resonance Phenomena of Nonlinear Feedback Control Systems, Joint Autom. Control Conf., N. Y.. 1962.

19. Shirakawa H. Stability of a Certain Class of Third-Order Nonlinear Differential Equations, IEEE Trans, on Autom. Control.. 1968, AC-I3, pp. 202-203.

20. Murty I. S. N., Deekshatulu B. L. Method of Variation of Parameters lor Overdamped Nonlinear Systems. Int. J. Control, 1969, 9, pp. 259-266.

21. Kontos J., Tzafestas S. On the Transient Performance of a Class of Second-Order Limit-Cycling Control Systems. IEEE Trans, on Autom. Control. 1970, AC-15, pp. 376-378.

22. Soudack A. C, Tarham P. O. D. Further Results on Approximate Solutions of Nonlinear, Nonautonomous Second-Order Differential Equations . Int. J. Control. 1970, 12, pp. 763-767.

23. Csaki F. Az allapotmodszer alapjai (Fundamentals ot the State-Space Method). Elektrotechnika, 1971, 64, №. 1-3, pp. 26-38.

Часть II. МЕТОДЫ ЛИНЕАРИЗАЦИИ

Простейшим методом изучения нелинейных систем является линеаризация. Суть ее состоит в том, что нелинейная система заменяется эквивалентной линейной. Очевидно, линеаризованная модель не может полностью заменить нелинейную систему, но в некоторых отношениях поведение линеаризованной модели может быть почти идентичным поведению нелинейной системы. Таким образом, имеется возможность применить некоторые хорошо разработанные методы анализа линейных систем для изучения линеаризованных моделей [47*, 48*, 141*, 149*].

В данной части книги описываются четыре типа линеаризации. В технических науках, включая теорию управления, предполагается, что отклонения от некоторой рабочей точки малы, и нелинейные характеристики заменяются эквивалентными линейными. В этом случае говорят о линеаризации вблизи рабочей точки, или о касательной аппроксимации; линеаризованная модель исследуется при малых сигналах (малых отклонениях) [1].

Второй метод, называемый методом описывающих функций [47*, 48*, 51*, 108*, 137*, 149*], или гармонической линеаризацией [65*, 66*], линеаризует нелинейную систему ие во временной области, а в частной. Он широко применяется в теории управления. Суть его состоит в том, что рассматривается только основная составляющая выходного сигнала нелинейного преобразователя, а высшие гармоники отбрасываются. Применение этого метода оправдано в том случае, когда преобразователь имеет характеристику фильтра низких частот.

Третий метод, называемый статистической линеаризацией, также применяется во временной области [49*, 75*, 119*]. Нелинейная система заменяется эквивалентной линейной моделью в предположении, что возмущения имеют гауссовское (нормальное) распределение.

Наконец, четвертый метод является комбинацией гармонической и статистической линеаризации. Поэтому он называется

методом комбинированной, или совместной, линеаризации [75*, 119*J,

Третий и четвертый методы используются главным образом в теории управления.

1. ЛИНЕАРИЗАЦИЯ ВБЛИЗИ РАБОЧЕЙ ТОЧКИ. КАСАТЕЛЬНАЯ АППРОКСИМАЦИЯ

В теории управления для исследования стационарных линейных систем были разработаны эффективные методы, основанные главным образом на анализе и синтезе в частотной области. К сожалению, обычные методы в общем случае не могут быть использованы для исследования нелинейных систем.

Однако, если колебания нелинейной системы достаточно малы, а статические характеристические кривые непрерывны и дифференцируемы в окрестности данной рабочей точки, то нелинейная система может быть линеаризована вблизи этой рабочей точки [1, 2]. Параметры линеаризованной системы сравнительно легко вычислить или найти по графику. После этого к системе, линеаризованной таким образом, могут быть применены при малых колебаниях хорошо известные частотные методы. Следует, однако, подчеркнуть, что успех линеаризации вблизи рабочей точки зависит от того, достаточно ли малы на самом деле колебания в нелинейной системе, чтобы замена ее линейной моделью была допустима.

1.1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ЛИНЕАРИЗАЦИИ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ В РЯД

Пусть уравнение

у =g(Xi, х^, ... , х„) (1.1-1)

описывает статическое (или динамическое) поведение преобразователя, где г/ -выходной сигнал этого преобразователя, г Xi, ..., Хп могут представлять собой переменные состояния (или входные сигналы) системы [92*]. Функция g многих переменных обычно нелинейная. В некоторой окрестности рабочей точки линейная модель может хорошо аппроксимировать нелинейную систему при малых отклонениях независимых переменных. Уравнение линеаризованной модели имеет вид

Ду Ki + /С2 + ...+К„ Дх = i /С,- Ах (1.1-2)

где А.у и AXi (t=l, 2, ..., п) представляют малые отклонения в окрестности рабочей точки, а Кг (t=l, 2, ..., п) называются коэффициентами линеаризации. Геометрически это означает, что гиперповерхность (1-1-1) заменяется гиперплоскостью (1.1-2), касательной к данной гиперповерхности в рабочей точке. По-

этому линеаризацию вблизи рабочей точки называют также касательной аппроксимацией. Если рассматривать Дг/ как выходную переменную, а ts.Xi (/=1, 2, ..., п) как входные переменные, то постоянные Ki ( =1, 2, ..., п) называются линеаризованными коэффициентами усиления. Координаты рабочей точки удовлетворяют уравнению

Y=g{X, Х^, Х^). (1.1-3)

Очевидно, что

у Г=Ду, Xi~XiLxi (г=1, 2, ... , ft).

Заметим, что линеаризованное соотношение (1.1-2) заменяет в окрестности рабочей точки как нелинейное уравнение

Ду g(X,-\-x Х^Л- х„) - Г, (1.1-4)

так и уравнение для конечных приращений

Ду-Д^(Дх1, Дх ). (1.1-5)

Для правильного определения коэффициентов усиления /Сг(1=1, .. ) необходимы данные в аналитической или графической форме о нелинейном процессе. Из исследования процесса управления мы должны определить рабочую точку и область изменения переменных, чтобы установить возможность линеаризации для реальных отклонений переменных в системе. Наконец, нужно оценить ошибку, вызванную линеаризацией.

Обычно прибегают к двум способам аппроксимации: методу касательной аппроксимации (разложению в ряд Тэйлора) и аппроксимации по методу наименьших квадратов. При небольшой нелинейности оба метода приводят к почти одинаковым результатам. Первый метод проще, зато второй точнее. Второй метод, кроме того, применим при несколько больших колебаниях, но его значительно сложнее использовать.

Если нелинейная функция g является аналитической (т. е. непрерывной и бесконечно дифференцируемой) в рабочей точке или в ее окрестности, то она может быть разложена в ряд Тэйлора. Ряд Тэйлора для функции п переменных

в окрестности рабочей точки М с координатами

(Aj, А'г, .... Х^

имеет вид

1=1 1=1

(x-;r,)(x,.-;r,-)+ .... (1.1-6)

где частные производные берутся в рабочей точке М-

Ограничиваясь малыми приращениями вблизи рабочей точки, можно отбросить члены высших порядков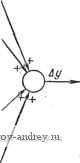

(1.1-7)

Рис. 1.1-1. Блок-схема линеаризованной системы. Следовательно, окончательно получаем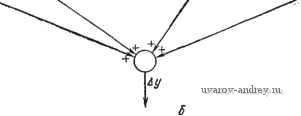

Это приближенное соотношение устанавливает линейную связь между приращениями (разностями) Ау и ЛлГг [92*]- Коэффициенты пропорциональности (т. е. коэффициенты линеаризации) являются частными производными в рабочей точке М.

Рассматривая приращения hxi в качестве входных переменных, а приращение Дг/ в качестве выходной переменной, уравнение (1-1-8) можно представить в виде блок-схемы, показанной на рис. 1.1-1, а и б, где

м

(г = 1, 2, ... , п)

(1.1-9)

представляют собой коэффициенты усиления, определенные как частные производные в рабочей точке.

Результат отбрасывания членов высшего порядка малости, т. е. ошибок усечения, можно оценить с помощью суммы членов второго порядка малости ряда Тэйлора.

Перепишем уравнение (1.1-1) в виде скалярного уравнения с векторным аргументом

y = g-(x). (1.1-10)

Тогда линеаризованное уравнение (1.1-8) можно записать в форме скалярного произведения

Ду =i grad U Дх = vgU Дх = -g

(1.1-11)

или (см. разд. 1.4, ч. V) в матричной форме Ду: [gradj]тдx=[v

тдх = dg

м

Дх, (1.1-12)

где gradg представляет собой градиент (вектор-столбец) скаляра g; V-вектор-столбец оператора набла {[д/дх,...

д1дх ), а Т означает транспонирование (от матрицы-столбца к матрице-строке, и наоборот). Очевидно,

grau g = jg:

dg .dx

L -1

gradg=[vgr =

дх \

Уравнение (1.1-12) можно также записать в виде

(Некоторые основные -сведения из матричной алгебры и векторного анализа даны в разд. 1, ч. V.)

Исследуем теперь преобразователь со многими выходами, статическое или динамическое поведение которого описывается системой из q уравнений с п переменными:

Ух = gx (-1, 2. , Хп\ Ус= gq i.Xx, 2. . Х„).

(1.1-14)

Эта система нелинейных уравнений может быть записана в виде единственной векторной функции с векторным аргументом

y = g(x).

Допустим, что произвольные нелинейные функции gi, gq могут быть разложены в ряд Тэйлора в окрестности рабочей точки М с координатами X=[Xi, Xz, ..., Х^. Тогда, разлагая их в ряд и отбрасывая члены высшего порядка малости, получим

п

У=g (X) g (X) -ь 2 L -

где

является вектором с q составляющими, т. е. Xl-матрица-столбец

Если ограничиться малыми отклонениями вблизи рабочей точки М, то получим

y-g(X) = y-Y = Ayi2 -

М

Дх,. (1.1-16)

Это выражение устанавливает линейную связь между приращениями htjj и hXi, или соответственно между Ду и Дх. Коэффициенты пропорциональности (т. е. коэффициенты линеаризации) являются частными производными в рабочей точке.

Рассматривая отклонения Длт; в качестве входных переменных, а отклонения Аг/j в качестве выходных переменных, можно

построить блок-схему линеаризованной системы

Дхп

... Дхг

... Дх

(1.1-17)

где

г = 1, 2, ... , п,

м' /= 1, 2, 9

представляют собой коэффициенты усиления, вычисляемые по частным производным.

к

К

а В

Рис. 1.1-2. Блок-схема линеаризованной системы.

При малых отклонениях вблизи рабочей точки Ш система уравнений линеаризованной модели преобразователя со многими переменными имеет вил

Ду1 ~ Кп + /С,2 4- ... + Кп Ах ,

Ду2 t=i /2! + 22 А-2 4- . + К2п А-

: (1.1-18)

АУд - 91 + ?2 А^2 + +? Ах или в векторной форме

Ду~КДх = АДх, (1.1-19)

где Ду и Дх-соответственно 9XI и /гXI векторы-столбцы (матрицы-столбцы), а К = А-прямоугольная матрица qXn. (если q = п, то квадратная матрица), элементами которой являются коэффициенты усиления Kji- Графическое представ- ение уравнения (1.1-19) дано на рис. 1.1-2, а м б. Элементы

матрицы К=А могут быть определены из уравнения (1.1-17). Матрицу А=К можно записать (разд. 1.4, ч. V) также в следующем виде, используя вместо скалярного произведения матричное:

A = K = J(g, x)l=gv U =

дХп

м

dggV

dgi dx

dgi dgi

dx dx2

dgg dgg

dxi dx2

dgi dxn

dx

(1.1-20)

Матрица K=A, составленная из частных производных, известна как якобиан и часто обозначается через J [35*, 46*, 135*, 145*, 151*]. Таким образом, вместо уравнения (1.1-12) для преобразователя с одним выходом имеем следующее уравнение для преобразователя со многими выходами:

м

(1.1-21)

1.2. ВТОРОЙ МЕТОД ЛИНЕАРИЗАЦИИ

Вместо того чтобы непосредственно определять частные производные, на практике линеаризацию часто выполняют следующим образом.

Выразим независимые переменные Хг через приращения Ал; относительно координат Хг рабочей точки

Xi = Xi -Ь LXi,

а зависимые переменные У) представим в виде

При подстановке этих выражений в исходное соотношение упрощается запись координат рабочей точки. При этом члены, содержащие произведение или степень приращений, отбрасываются. В результате получается линейное выражение для приращений.

Пример 1. Линеаризуем соотношение yg{,Xi, XijXiXz вблизи рабочей точки Y=g{Xi, Хг). Пусть

у = К -Ь Ду, х, = А', -Ь Д^!, 2 = Л'г -Ь х^.