меняются дифференциальные уравнения в частных производных для описания и решения задач оптимального управления системами с транспортным запаздыванием.

Рассмотрим систему, описываемую дифференциально-разностным уравнением

x(0 = f(x(0, х(-т), и(0, О (1-5-1)

с начальным условием

х(0 = Хо(0, €[-т, 0], (1.5-2)

где t - чистое запаздывание.

Перейдем от этой записи к системе обыкновенных дифференциальных уравнений и уравнений в частных производных

x(0 = f(x(0, z(0, u(00. (1-5-3)

+-0 (,.б-4)

С начальными и граничными условиями

х(0) = Хо(0),

У(0, 8) = Уо(8) е[0>

у(, 0) = х(0 tO,T

z(0 = y(. ) t& О, Т

(1.5-5)

где у (д) = Хо(-О). Подставляя решение у(, т) уравнения (1.5-4) в соотношение (1.5-3), нетрудно убедиться в эквивалентности этих представлений. Переменная & и вектор у(, &) выполняют роль фиктивной координаты и вектора состояния для случая, когда в системе, определяемой уравнением (1.5-1), отсутствует транспортное запаздывание.

Преимущества второго определения очевидны, так как уравнение (1.5-4) можно применить для описания более общих процессов транспортного запаздывания. Для этого достаточно ввести в это уравнение некоторый множитель g{t, &) и соответствующим образом изменить правую часть, чтобы получить уравнение

Л-ёИ, &) = h(y(, &)w( Ь), и Ь),

€[0, П.. €[о. (1-5-6)

с теми же начальными и граничными условиями (1.5-5) и сохранить прежнюю систему обыкновенных дифференциальных уравнений (1.5-3). Здесь x(t) есть п-мерный вектор состояния системы с сосредоточенными параметрами, у(, &)-п-мерный вектор состояния процесса с транспортным запаздыванием,

Система с сосредоточенными параметрами

u(t)

z(t}

z(0 = y(, т)-n-мерный выход, который одновременно является входной переменной для системы (1.5-3), и СО-г-мерный вектор

управления системой с сосредоточенными параметрами и w(, €)-s-мерный вектор управления транспортным запаздыванием (рис. 1.5-1).

Предполагается, что функции f и h имеют непрерывные вторые производные по всем аргументам и удовлетворяют условиям Липшица. Функция g{t, &) непрерывна и, кроме того, g{t, 0) >0, g{t, т)>0. Производная вектор-функции f по векторной переменной Z не зависит явно от вектора управления и. Допустимые кусочно-непрерывные управления и, w принимают значения в заданных выпуклых областях и е f/, V/ eW. Можно показать [264], что для заданных векторов допустимых управлений и и w траектории x(t) и у(, &) однозначно определяются своими начальными и граничными условиями.

Минимизируемый функционал стоимости задается в виде

z(tH(t.i:)

Процесс транспортного запаздывания

Рис. 1.5-1. Блок-схема системы с транспортным запаздыванием.

/ = kx(7)-fjr {Щу{Т,Ь)с1Ъ + ni(Oy(, )dt. (1.5-7)

Определим теперь скалярные функции Гамильтона: ф(х, гр, Z, U, t, &) = ipf (х, Z, U, t), Kiy, Ь w, t, &)=/h(y, w, t, &)

или

Hp(x, p, z, u, 0 =P*(x, z, u, t), Kpiy, q, w, t, b) = qh(y, w, i, &),

где ij5=-p, (j)=-q-вспомогательные векторы. Они удовлетворяют следующей системе уравнений:

(1.5-8)

(1.5-9)

-g{t,

дч{и &) d(g{t. %)(f{t. Щ 0t 5)

(1.5-10) (1.5-11)

4.(7, &) = -/(&) при&£[0, т].

lit) = ip{t,0) при /€[0,7], (1-5-12)

= g{t, x)if{t, т)+ m(0 при /е [О, 7]. Аналогичная система для вектор-функций р и q имеет вид

- + Sit, 0)71(0, (1.5-13)

а/ as --- (1-5-14)

Р(П = к,

q (7, &) = !(&) при С [О,.],

1-3(0 = q(,0) при /£[0, 7], (1.5-15)

-аГ = )Ч(. 0-/?г(0 при /[0, 7].

Для оптимальности допустимых векторных управлений и и W необходимо, чтобы в случае принципа максимума

(х , z , u , О > Яф (x , -фО, z , u, 0; € [0. 7],

(1.5-16)

ф(у . q . w , t, b)>K{x q , w, , &); Y6[0, П.¥ 6[0,

и в случае принципа минимума

Яр(х , р , z , и , 0<Я^,(х°, р , z , U, 0; [О, 7],

(1.5-17)

Кр{л^, q , w , /, Ь) < /р(хО, q , w, t, Щ; t[0, 7], у е [О, А-

Если функции f и h представимы в сепарабельном относительно векторов состояния и управления виде

f(x, Z, U, 0 = *Лх. Z, t) + hiy) h(у, W, /, Ь) = (у, /, Ь) + h, (w) -

и, кроме того, fo и - линейные функции векторов состояния, то необходимые условия максимума или минимума становятся также достаточными.

Предложенный метод можно легко распространить на случай нескольких процессов с транспортным запаздыванием. При

этом функционал стоимости задается соотношением

/ = к^х (Г) + Д [ 1J (Г. &,) d%j + 2 J (О у, О,) rf,

(1.5-19)

а уравнения системы имеют вид

= f (X (О, Z, (О.....z , (О, U (О, 0. (1.5-20)

+ у)-Т^ = Ь/(у,( 8/), W,(, ОД л О,)

при /=1, 2, ..., ттг, [О, Г], &у^[0, т^], (1.5-21) х(0) = Хо(0), У,- (о, 0 = Vjo {%) при bj 6 [О, у,.(, 0) = х(0 при^е[0, П.

(О = У/ {t, т,-) при С [О, П. € [о, ,1. Гамильтонианы задаются равенствами

ф(х, Zi, ..., z , u, t) = ifTf (X, Zi, ... . z, u, 0> (1.5-23)

фЛУу. Р/. W/ > y) = ФуЛУ/ wy, t, &/) (/=1, 2, w).

(1.5-24)

Кроме того,

=-1r + i 0)1,(0. (1.5-25)

--ш-+-Щ-

где

Ф,(Г, &у) = 1Л у) при &,[0, т,].

Фу(ло) = ДО при С [о, Г]

*=&(а &у)фЛА =.) + тЛО при 610, П у6 [о. -у].

(1.5-27)

Гамильтонианы можно также определить формулами Я^,(х, р, Zi, ..., г^, U, i) = pTf (х, zi, .... z , u, 0. (1.5-28) ру(Уу. Чу. w,-, t, О,) = Jh,(y w t, bj) (1.5-29) 0 = 1, 2, .... m).

в этом случае вспомогательная система уравнений имеет вид

---%Л^НШ (1.5-30)

дГ Щ ---

где

Р(П = 1<.

Яу(Г, bj) = -\j(%j) при &,е[0, х,1.

(\,{t,0) = -ji,t) при [О, П.

(1.5-32)

= &(. )qy(, /)-m,(0 при /е[0. Г]. &у^[0.

дНр

Замечание 1. Рассмотрим систему, задаваемую соотношениями (1.5-1) и (1.5-2) или эквивалентным представлением (1.5-3) - (1.5-5). Пусть функционал стоимости 1=Хо(Т). Тогда

Яф = я1,Ч НррЧ, (1.5-33)

/Сф = 0, Кр= О, (1.5-34)

где

+ + (0) = ° Т+- + Ч(.0) = 0. (1.5-35)

й аГ~~ а^ т а ц.о-db)

-(р(/, .) = 0, -q(/, т) = 0. (1.5-37)

Решая уравнение (1.5-4) с граничными условиями (1.5-5), получим

z(0 = y(. ) = У(-. 0) = х(/-4 (1.5-38)

Из уравнения (1.5-36) имеем Ф(/,&) = (/-&, 0) или q{t, b) = q{t- Ь, 0). Используя соотношения (1.5-37), получим

Ф(, 0) = Ф (/ -f т, т) = / . 6 [О, Г-т] или (1.5-39)

q(.0) = q(/-f...)==-4i. €[0.

Подставляя выражения (1.5-38) и (1.5-39) в (1.5-3) и (1.5-35) и учитывая, что для t=T значения ф {t,=0,q(t,О) = О,тогда как (р {t, 0) =0, q(/, 0) = 0 для Т - x<t<T, придем к системе соотношений

= f(x(0, х(-.), u{t), t).

или

£1W dt

dp(.t) dt

dHpit) dHp(t + t)

дх dHp{t)

(1.5-40)

Условие максимума или минимума состоит в определении такого вектора управления u>(t), для которого гамильтониан Hw (или Яр), заданный равенствами (1.5-33), достигает максимума (минимума). Вспомогательное уравнение (1.5-40) и сформулированное условие максимума те же, что и в работе Понтрягина [112*]; условие минимума и вторая группа вспомогательных уравнений (1.5-40) получаются непосредственно. В соответствии с условиями трансверсальности векторы (Т) и р{Т) должны быть ортогональны к касательной плоскости множества цели в точке х(Т).

Замечание 2. Системы с нестационарным запаздыванием, заданные дифференциально-разностным уравнением

X=f (X (0), X ( - О, (0), ..., X (-& (О, U (0), (1.5-41)

можно также привести к виду (1.5-20), выбрав соответствующим образом функции gj{t, &) и hj{t, Ь):

hy(&y(0) = 0,

ft /.чч \{t)-%j(t)[dtj{t)ldf\

gj it, (t)) =--, у = 1, 2, ..., ттг, (1.5-42)

zy(0 = yy(, 1).

Эквивалентность соотношений (1.5-41) и (1.5-20) с (1.5-42) следует из условий

у J {t, Ь,) = X {t-bfj {t)\ у - 1, 2, .... m.

Пример 1. Рассмотрим систему управления температурой (рис. 1.5-2). Температура в резервуаре 1 регулируется за счет

управляемого подогрева в резервуаре 2 и циркуляции жидкости между этими резервуарами. Учитывая потери тепловой энергии как в резервуаре 1, так и в процессе теплоотдачи циркулирую-

Резердцар 1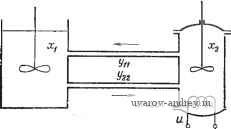

Резер6уар2

Рис. 1.5-2. Система управления температурой с транспортным запаздыванием.

щей по трубам жидкости, придем к следующей системе уравнений:

X, (0=-1 (xi (t) - G,) + k (У22 {t, t) - X, (t)), X, (0) = 0,

X2 (0 = 2-4 (-2 (0-Уи (t, ))> -2 (0) = 0,

(1.5-43)

(1.5-44)

-if+3 = - /3 (У22 - e,),

Уп(0, 8i) = 0, у22(0, &2) = 0,

y (/, 0) = Xi, У22(/, 0) = X2,

где Xi и -температура в резервуарах i и 2; и У22 - температура в трубопроводах; (О^и^ы*) - вводимое тепло; ©е - внешняя температура; h и /г - константы.

Цель оптимального управления состоит в том, чтобы в конечный момент времени t=T при минимальных затратах вводимой тепловой энергии свести к минимуму отклонение температуры в резервуаре 1 от заданной температуры Ха. Для такой постановки функционал стоимости определяется выражением

т

I = (xi {Т)-Ха)+с^ и? it)dt. (1.5-45)

о

Гамильтонианы, которые требуется максимизировать, задаются в виде

Яф=фои' (О + Ь \-kx - G,) -f /1 (У22 {t, t) - x,)\ -f

+ Ф2 [2 - 4 (-2 - Уи {t, ))1> (1.5-46) /Сф=-?114(У11-0.)-?224(У22-в,). (1.5-47)

Вспомогательные уравнения и граничные условия имеют следующ,ий вид:

Фо = 0, Ф1 = [k, + /1) ti - з?22 it, 0), Ф2 = - 3%2 {t, 0), фо(Г)=-с, i(r)=-2(j<:,(r)-j<:J, Ф2(П=0; (1.5-48)

a<j).

(1.5-49)

= ?n(. ) = -ф2(0. MO. n.

?,l(7, )=0, Cp22(7. 2) = 0.

Оптимальное управление должно удовлетворять условию максимума, следовательно.

и (0 =

2с и*.

*Фз<0,

0<fe< *.

(1.5-50)

Для определения траектории 2 необходимо, используя формулу оптимального управления (1.5-50), решить совместно вспомогательные уравнения (1.5-48) и (1.5-49), а также системы уравнений (1.5-43) и (1.5-44).

В общем случае решение этой задачи требует применения вычислительных методов, однако для рассматриваемого примера уравнения (1.5-44) и (1.5-49) могут быть решены аналитически:

вЛ&-ехр(Ш, t\0,фA,

ехр(-/зт/-з) Xi{t - т/з) + (1.5-51)

-f ©Л/ - ехр (- /зт/з)), te[T/3, Г],

( ехр(-/зт/з).ф,(+т/з), Ш[0, Т-хЩ,

О, [Г-т/з, Т].

(1.5-52)

Подставляя выражения (1.5-51) и (1.5-52) в уравнения (1.5-43) и (1.5-48), придем к совместным системам обыкновенных дифференциальных уравнений, на основе решения которых

Mi, 0) =

должен быть определен закон оптимального управления. Значение % в конечный момент времени есть функция конечного условия Хи которое, как правило, не известно до тех пор, пока не найдены решения этих уравнений. Итак, для решения сформулированной задачи оптимального управления требуется использовать итеративную вычислительную процедуру, которая выглядит следующим образом:

1. Выбрать значение Xi(T) и вычислить %pi(T) = 2-2(Xi(T)-

-Xd).

2. Проинтегрировать вспомогательное уравнение (1.5-48) от t=T т t = 0 и определить управление и° (t) из соотношения (1.5-50).

3. Проинтегрировать систему уравнений (1.5-43) от =0 до t=T, используя найденные значения il5i(0) и функцию управления u°(t).

4. Сравнить полученное таким образом значение Xi(T) с заданным первоначально.

Если эти значения достаточно близки, прекратить вычисление, в противном случае требуется изменить выбранное первоначально значение Xi(T) и повторить вычислительную проце-ДУРУ-

Пример 2. Рассмотрим систему первого порядка с одним запаздыванием

x(t) = -x{t)-Kxii--z) + Kuit),

\u{t)\<l,

которая соответствует системе с обратной связью с передаточными функциями K/{s+\) по прямому каналу и ехр(-st) в цепи обратной связи. Для управления, оптимального по быстродействию, гамильтонианы запишутся в виде

= - 1 - Ф (О X (О - /Сф (О x{t~) + К'Р if) и it) (1.5-54)

или

Ир=\- p{t)x{t)-Kp{t)x(,t--z) + Kp{t)u{t). (1.5-55)

Оптимальное по быстродействию управление

0(0 = sign /Сф it) = - sign [Kp{t)\, t[Q, Т\. (1.5-56)

Из соотношений (1.5-40) получим уравнение для вспомогательной переменной

. \Ht) + KW + ), t\o,T~.\,

или

Дальнейшие вычисления целесообразно проводить на вычислительном устройстве.

ЛИТЕРАТУРА

1. Болтянский В. Г., Гамкрелидзе Р. В., Понтрягин Л. С. К теории оптимальных процессов, ДАН СССР, 1956, 110, № I.

2. Болтянский В. Г. Принцип максимума в теории определенных процессов, ДАН СССР, 1958, 123, Ns 2.

3. Понтрягин Л. С, Оптимальные процессы регулирования. Успехи мат. наук, 1959, 14, Ks 1, стр. 3-20.

4. Болтянский В. Г., Гамкрелидзе Р. В., Понтрягин Л. С. Теория оптимальных процессов, I, Изв. АН СССР, сер. мат., I960, 4, № I.

5. Boltyanskii V. G., Qamkrelidze R. V Mischenko E. F.. Pontryagin L. S The Maximum Principle in the Theory of Optimal Process of Control, Proc First. Intern. Congr. Autom. Control, Eyre and Spottiswoode (Publishers) Ltd. London. 1961.

6. Колмогоров A. H., Мищенко e. Ф., Понтрягин Л. С. Об одной вероятностной задаче оптимального управления, ДАН СССР, 1962, 145, № 5.

7. Болтянский В. Г. Достаточные условия оптимальности и обоснование метода динамического программирования. Изв. АН СССР, сер. мат., 1964, 28, № 3.

8. Болтянский В. Г., Ройтенберг Е. Я. Пример синтеза нелинейной системы второго порядка. Кибернетика, 1966, № 4, стр. 52-56.

9. Александров В. В. О применении аналоговых вычислительных машин для итерационного процесса определения в одной оптимальной системе. Вестник МГУ, сер. мат. и мех., 1964, № 4.

10. .VHopoB В. П. Принцип макси.мума для процессов с ограничениями общего вида, Автоматика и телемеханика, 1967, 28, № 3 и 4.

11. Aoki М. On Optimal and Sub-optimal Policies in the Choice of Control Forces tor Final-value Systems. IRE Trans. Autom. Control. 1960, AC-5, № 3, pp. 171-178.

12. Aoki M. Stochastic-Time Optimal Systems. AIEE Trans. Applications and industry, 1961. 80, Pt. П, pp. 41-44.

13. Аоки M. Проблема минимума нормы и некоторые другие методы оптимизации систем упрг1вления, в книге Современная теория систем управления, под ред. К. Т. Леондеса, М., изд-во Наука , 1970.

14. Arimolo S. Linear, Stationary, Optimal Feedback Control Systems, Information and Control, 1966, 9, № 1, pp. 79-93.

15. Astrom K. J., Bertram J. E. Current States of Linear Optimum Control Theory, J. SIAM Control, 1963. 1.

16. Athanassiades M. Smith O. J. M. Theory and Design of High Order Bang-Bang Control Systems. IRE Trans. Autom. Control, 1961, AC-6, pp. 125- 134.

17. Athanassiades M. Bang-Bang Control for Tracking Systems, IRE Trans. Autom. Control. 1962. AC-?, pp. 77-78.

18. Athanassiades M. On Optimum Linear Control Systems which Minimize the Time Integral of the Absolute Value of the Control Function (Minimum-Fuel Control Systems). MIT Lincoln Lab. Rept. 220-4, Lexington. Mass. May 1962.