Оптимальное быстродействие. В задаче оптимального быстродействия подынтегральное выражение имеет вид /о(х, и) = 1 и поэтому гамильтониан

Нр = \+ р^Ах -f р^Вц = 1 + xWp -f uTRTp. (1.3-7)

Дифференциальное уравнение относительно вспомогательной переменной рсо и его решение записываются в виде

р(0 = -АТр(4 (1.3-8)

р(/)=е-р(0). (1.3-9)

Вектор управления и входит только в последнее слагаемое гамильтониана; поэтому задача сводится к минимизации одного этого члена. Так, например, необходимое условие экстремума при отсутствии ограничений на управление состоит в том, чтобы

= в> = о.

Этот анализ приводит к практически бесполезному выводу, что р(0) = 0, р(0 = 0, а управление и-произвольно. Полагая же по определению

q(0 = bp() = bv%(0). (1.3-10)

получим, что гамильтониан достигнет минимума, если оптимальное управление удовлетворяет необходимому условию

vP{t) == -signq (0 = -signBTpO() (1.3-11)

или

5 (О = - sign it) (7=1,2...., г). (1.3-12)

Таким образом, оптимальное управление задается кусочно-непрерывной функцией, принимающей значения у == + 1 или и°. =-1 (/=1, 2, ..., г) в зависимости от выхода сопряженной системы.

Оптимальное управление как функцию времени можно было бы определить точно, если бы были известны временные зависимости р'со- Для этого требуется знать начальное р (0) или конечное р (Т) условия, которые являются нелинейными функциями граничных условий х(0) и х(Т) и не могут быть определены заранее. Для решения этой задачи был разработан геометрический метод так называемых поверхностей переключения, который рассмотрен ниже.

На рис. 1.3-1 приведена двухальтернативная блок-схема оптимальной системы линейного управляемого объекта для определения сопряженных переменных, В задаче оптимального

быстродействия переключающим элементом S является или двухпозиционное реле, или реле с зоной нечувствительности (рис. 1.3-2).

fadT с

АльтериатиВа!

Альтернатива 2 -Р

i>{t)-4(t)

p(thp{oHpmr

x(t)-x(0)Cc)dT

x(t)=Ax*Bu

Рис. 1.3-1. Блок-схема системы оптимального быстродействия.

Оптимальное управление расходом топлива. В задачах управления самолетами и космическими летательными аппаратами переменная управления u(t) - сила тяги или момент вращения-пропорциональна скорости расхода массы и, следовательно, ограничена. В связи с тем что общий запас топлива

-ч

Рис. 1.3-2. Переключающий элемент в системе оптимального быстродействия.

также ограничен, любые сложные движения или движение по курсу должны осуществляться с минимальным расходом топлива.

Рассмотрим задачу, в которой для управляемой системы [уравнение (1-3-1) и ограничение (1.3-3)] требуется определить оптимальное управление u°(t), переводящее систему из начального состояния х(0) в конечное состояние (Т) таким образом,

чтобы функционал, характеризующий систему (расходтоплива),

Т г J

I = J I uj {t) \dt-= j uT (0 sign u (0 dt (1.3-13)

принимал наименьшее возможное значение. (Очевидно, что время Т не меньше минимального времени Т .) Целевая функция

/о( ) = Д|иЛ01 =uT(Oslgnu(0 (1.3-14)

представляет сумму скоростей расхода топлива в единицу времени; интеграл от нее соответствует общему потреблению топлива. Для такой задачи гамильтониан

Ир = sign U + рт Ах -f ртВц = sign и +

+ xWp + цтвтр. (1.3-15)

Таким образом, дифференциальное уравнение относительно вспомогательных переменных и его решение совпадают с уравнением (1.3-8) и решением (1.3-9). Функция состояния (1.3-15) принимает наименьшее значение при условии, что минимально выражение

цТ (t) sign u (t) + uT (t) q (t) = uT (t) [sign u () -f q (t)]. (1.3-16)

При этом необходимо различать два случая:

1) если \gAt)>\, то < (t) = - sign (t)

и (1.3-17)

2) если \q°it)<l, то 0(0 = 0,

где (0 (у'=1, 2, г) есть у-я компонента вектора q°(t). Эти условия можно выразить в виде соотношения

u(t) = - sgzm q° it) (у = 1, 2, ... , г), (1.3-18)

где sgzm - сокращение от латинского signum functio cum zona mortua (знаковая функция с зоной нечувствительности); иногда используют также обозначение dez (dead -zone function - функция зоны нечувствительности). Соотношение (1.3-18) можно записать также в виде векторной функции векторного аргумента

иО(0=-sgzmq (0. (1.3-19)

Следовательно, управление, минимизирующее расход топлива, задается кусочно-непрерывной функцией, принимающей значения uPj = + \, и°=0 или и^=-1 в зависимости от выхода сопряженной системы.

Хотя точную временную зависимость и (t) найти трудно, так как для этого необходимо определить начальное условие р°(0) как функцию состояния, однако уже сейчас можно ответить на некоторые относящиеся к рассматриваемой задаче вопросы. Например, можно заключить, что для оптимального управления требуется не более пары двухпозиционных клапанов типа включено- выключено (понятию отрицательного управления отвечает изменение направления движения сжигаемого топлива на обратное). Исследование функции приводит к некоторым

дополнительным выводам. Если собственные значения 5, матрицы А - действительные отрицательные и различные числа, то p(t) обращается в нуль самое большее п-[ раз в зависимости от начальных условий р?(0). Так как q°.-(t) представляется линейной комбинацией компонент p4(t), то уСО также может обращаться в нуль не более чем п- 1 раз. Если же матрица А

Рис. 1.3-3. Переключающий элемент в системе оптимального управления расходом топлива.

имеет комплексные собственные значения, получить аналогичную оценку числа перемен знака не представляется возможным. Из непрерывности функций qj(t) следует существование времени перехода по управлению 5 = 0 между периодами с управлением = -Ы и - 1.

Блок-схема оптимальной системы линейного управляемого объекта (рис. 1.3-3) остается той же самой, только в этом случае при оптимальном управлении на минимум расхода топлива переключающим элементом S является трехпозиционный переключатель, или реле с зоной нечувствительности (рис. 1.3-3).

Оптимальное управление на минимум расхода энергии. Существует целый класс задач управления, в которых квадрат управляющей переменной (О пропорционален отдаваемой мощности, а результат интегрирования этого квадрата по времени пропорционален затраченной энергии. Например, в электрической цепи такой переменной u{t) может быть напряжение или; электрический ток.

Предполагая, что управляемая система имеет те же самые уравнения, что и выше, найдем оптимальное управление uCOs которое переводит систему из начального состояния х(0) в ко-

нечное состояние х.(Т) таким образом, что функционал стоимости J

/= 4-( uT(Ou(0 (1.3-20)

принимает наименьшее возможное значение при ограничениях (1.3-3). В этом случае целевая функция имеет вид

/о(и) = иТи. (1.3-21)

Гамильтониан оптимальной задачи на минимум расхода энергии

Hp = -g-uu + рТ Ах + рТ Ви = 4 u+xWp + и^ВТр. (1.3-22)

Получаемые отсюда сопряженное дифференциальное уравнение и переменная q(0 идентичны приведенным ранее соотношениям (1.3-8) и (1.3-10). Функция состояния принимает наименьшее возможное значение при условии, что выражение

i- uT (О U (О + W q (О = (О [4- (О + q (О] (1-3-23)

также достигает минимума. При этом снова необходимо различать два случая. Если \(}j(t)\<i, то, исходя из необходимого условия экстремума

[т + / ()] = / + / = О'

найдем, что координаты управления, минимизирующего выражения (1.3-22), задаются соотношениями

°(0 = -И0; и°(01<1. (1.3-24)

Если же I qj(t) [ > 1, то рассматриваемый гамильтониан принимает наименьшее значение при условии, что

5 (О = - sign 5 (i), I it) I > 1. (1.3-25)

Переменная q°.{t) (/=1, 2, г) есть у-я координата вектора q{t). Заметим, что закон управления, задаваемый соотношениями (1.3-24) и (1.3-25), может быть выражен в форме

uO(0 = -satq (0, (1.326)

или

о (t) = - sat q. it) (у = 1, 2, ... , г), (1.3-27)

где sat - скалярная функция насыщения по скалярному аргументу, в то время как sat - соответствующая векторная функция векторного аргумента.

Блок-схема оптимального управления остается той л<е самой, что и на рис. 1.3-1, однако переключающим элементом 5 является нелинейный элемент с характеристикой типа насыщения (рис. 1.3-4).

Смешанный критерий. В рассмотренных выше трех задачах минимизируемый функционал стоимости (или целевая функция) зависел только от вектора управления. Это общая черта всех задач с условиями на конце и критерием, который не наклады-

Рис. 1.3-4. Переключающий элемент для управления с минимальной энергией.

вает ограничений на переменную состояния. Рассмотрим теперь несколько иную задачу. Допустим, что целевая функция может быть представлена в виде суммы двух компонент

/о(х, ii)=/o(x)-f/o(ii). (1.3-28)

В этом случае гамильтониан

Hp = /о (X) -Ь /о ( )> р^ Ах + рТВи. (1.3-29)

Минимизируя функцию состояния по переменной вектора управления U, получим тот же закон управления, что и раньше, если только

1, или и sign 11 или 1 т

Дифференциальное уравнение для вспомогательного вектора рсо изменится: теперь оно запишется в соответствии с выражением (1.3-6). Следовательно, для сепарабельной целевой функции закон управления в задачах на минимум расхода топлива, минимум расхода энергии и в задаче оптимального быстродействия остается прежним.

В дальнейшем основные случаи, которые следует различать при управлении описанными выше линейными объектами, будут рассмотрены подробно. Оказывается, что поверхность переключения к(х (0) и правило оптимального управления, задаваемое

одним из равенств иЧО = -signk(x<(0). °CO = - sgzmk(x (0) или M{t) = -satk(xCO), можно реализовать, включив в блок-схему соответствующие нелинейные элементы. При этом отпа-

дает необходимость в решении дифференциального уравнения для вспомогательного вектора. Таким образом, удается обойти трудности, возникающие при решении сопряженного дифференциального уравнения, характеристические корни которого положительны или имеют положительную действительную часть (при этом даже малые ошибки в определении вектора начальных условий р(0) приводят к существенным искажениям). Использование поверхностей переключения позволяет значительно

о

=>

Рис. 1.3-5. Блок-схема системы оптимального управления с поверхностью

переключения.

упростить решение проблемы за счет обратной связи, которая включена в блок-схему (рис. 1.3-5). Построение нелинейной функции к(х) переключающей поверхности можно осуществить на модели, а также с помощью цифрового или аналогового вычислительного устройства.

1.4. СВОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ

Прежде чем приступить к детальному обсуждению, приведем некоторые определения и теоремы для трех рассмотренных выше фундаментальных задач управления (оптимальное быстродействие, оптимальный расход топлива, оптимальный расход Энергии) [105, 158, 168, 211, 230]. Сначала рассмотрим нелинейную систему уравнений [31]

i = f(x(0, 0 + В(х(0, t)uit),

y(0 = g(x(0)-

(1.4-1)

Системы, оптимальные по быстродействию. Задача об оптимальном быстродействии называется нормальной, если коорди-

q](.t) = /M)biM(.t),t) (1.4-2)

обращается в нуль лишь в счетном числе точек. Если же найдутся промежутки времени (подынтервалы), такие, что9 (0 = 0, тогда задача называется вырожденной [141, 143, 246].

Для нормальных задач имеет место так называемый релейный принцип [82-86, 181-183, 186, 187]: вектор оптимального управления задается равенством

и {t) = - sign qO (О = - sign ВТ (X (О, О Р {t), (1.4-3)

или

5- (О = - sign i [t) bij (х {t), t). (1.4-4)

Таким образом, отдельные компоненты вектора не могут принимать других значений, кроме +1 или -1. Заметим, что выражение для вектора оптимального управления не зависит от граничных условий.

Управление иэ(1) называется экстремальным, если соответствующий вектор состояния y?{t) и вспомогательный вектор p(t) удовлетворяют необходимым условиям оптимальности. Векторы х^(/) и р^(0 называются экстремальными траекториями состояния и дополнительной переменной соответственно.

В общем случае для одной и той же задачи могут существовать несколько экстремальных управлений. Каждое экстремальное управление дает траекторию, которая может быть оптимальной либо локально, т. е. является наилучшей среди всех близко расположенных в некоторой ограниченной области траекторий, либо глобально. Так как экстремальные управления удовлетворяют необходимым условиям оптимальности, то можно отметить, что если существует единственное оптимальное управление и (О и нет других локально оптимальных управлений, то существует только одно экстремальное управление иэ(/), которое одновременно является и оптимальным u{t) =vP{t). Следовательно, если другие локально оптимальные управления отсутствуют, то принцип минимума определяет необходимое и достаточное условие оптимальности.

Если глобально оптимальные управления отсутствуют, но существуют т локально оптимальных управлений, то имеется точно т экстремальных управлений. Следовательно, из существования экстремального управления не вытекает существование глобально оптимального управления.

Если же оптимальное управление существует, то его можно

найти, выбрав экстремальное управление, отвечающее минимальному времени Р.

Таким образом, при решении задачи об оптимальном быстродействии требуется ответить на следующие вопросы:

1. Существует ли управление, оптимальное по быстродействию?

2. Единственно ли оптимальное управление?

3. Является ли задача нормальной?

4. Не содержится ли дополнительной информации в необходимых условиях?

Рассмотрим теперь класс линейных автономных управляемых объектов, задаваемых соотношениями (1.3-1). Обозначим через bj (/=1, 2, г) векторы-столбцы матрицы В. Предположим, что система полностью управляема. Поэтому она может быть переведена из любого начального состояния х(0) в конечное состояние х(Т) = 0 по крайней мере за ограниченное время Т. Это, однако, справедливо в том и только в том случае, если гиперматрица

G= [В, АВ, А^В, .... А -1 В] (1.4-5)

порядка пХгп содержит п линейно независимых векторов-столбцов. Задача об оптимальном управлении линейной автономной системой вырождена в том и только в том случае, если по крайней мере одна из матриц

Gj = [by, Ab,-. A-b,. ... , A -ib,.] (1.4-6)

порядка nXn является вырожденной, т. е. имеет ранг, меньший п. Задача нормальна, если ни одна из матриц Gj (у=1, 2, г) не является вырожденной. Необходимые и достаточные условия для нормальности задачи идентичны условиям нормальности системы [выражение (1.3-1)].

Если управляемая линейная система нормальна и если оптимальное управление и (t) существует, то такое оптимальное управление единственно.

Если собственные значения Si (г= 1, 2, п) матрицы А - действительные числа, а u(t) (/= 1, 2, .... г) - компоненты единственного оптимального по быстродействию управления и (t) (если оно существует), тогда знак кусочно-постоянной компоненты управления u(t) = ±l может изменяться не более чем п-1 раз. (Можно показать, что число нулей суммы п действительных экспоненциальных функций времени не превышает п-1.) Для случая комплексных собственных значений можно лишь утверждать, что число переключений конечно и зависит от начального условия х(0).

Кроме того, если линейная автономная система нормальна и существует оптимальное управление и (0. переводящее систему

из начального состояния х(0) в конечное состояние х(Т) = 0, то это оптимальное управление единственно.

Обозначим через Т°(х) минимальное время перехода из начального состояния х(0) в конечное состояние х(Г) = 0. Пусть /(т) -изохрона (кривая линия или поверхность), каждая точка которой удовлетворяет соотношению Т°{х)=х. Очевидно, что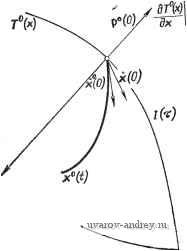

Рис. 1.4-1. Принцип оптимального управления (при оптимальном управлении usl/ вектор \(t) стремится к направлению наискорейшего убывания).

переход осуществлялся бы за кратчайшее время, если бы вектор скорости x(t) был направлен вдоль вектора grad Р(х). Для этого векторы

i(0) и c?7o(x)/c?xU=x(0)

должны быть параллельны и противоположно направлены. Скалярное произведение таких векторов равно абсолютному минимуму. Однако в пределах наложенных ограничений u(t) е U скалярное произведение может достигать только относительного минимума (рис. 1.4-1). Следовательно,

от (0)

;хт(0)

X = X (0)

X = X (0) ~ дх

Из уравнения (1.3-1) находим, что

х(0) = Ах(0)-ЬВи(0) и io(0) = Ах(0)-ЬВи (0)

(1.4-7)