в общем случае применение принципа максимума сводится к численному решению нелинейной двухточечной граничной задачи. Для системы, начальное и конечное состояния которой закреплены, это очевидно; в задаче с подвижными концами свободные координаты х(Т) приводят в силу условий трансверсальности к фиксированным компонентам (Т).

В наиболее общей формулировке задача синтеза оптимальных систем не имеет общего решения; однако известны многочисленные примеры решения этой задачи в различных частных постановках.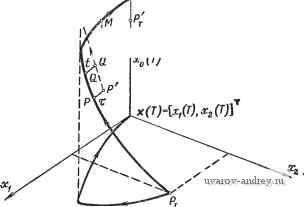

х(ОИхМг(0)] ,

Рис. 1.1-5. Геометрическая интерпретация принципа максимума.

Интерпретация принципа максимума. Выше показано (рис. 1.1-3), что если х (О - оптимальная траектория, тогда Хо(Т) = х°(Т)=1мтип. При этом не существует траектории, которая порождается допустимым управлением u(t) ef/, приводящим к меньшему значению критерия, например, в точке Т', отличной от точки Т (рис. 1.1-5). Этот принцип справедлив для любой промежуточной точки М траектории X (t). В противном случае траектория, проходящая через точку М', лежащую ниже точки М оптимальной траектории х° (t), была бы лучше оптимальной. Таким образом, точки, расположенные ниже траектории X (t), недостижимы.

предположим теперь, что оптимальное управление и С/) претерпевает отдельное изменение и*(0 = v = const в точке t=x - б/=т - еД/ в течение достаточно короткого промежутка времени 6/=еА/:

(V, 1 - е < < т,

где е - достаточно малая величина. (Разумеется, можно было бы также изучить влияние нескольких непересекающихся вариаций, заменив их одним возмущением, для которого проварь-ированная траектория не проходит через точку хСГ).) Приращение траектории бх(т) представлено вектором РР. Допустим, что в дальнейшем оптимальное управление не претерпевает никаких возмущений; тогда проварьированная траектория под действием управления и (О пройдет через точку Q, отличную от точки q (рис. 1.1-3). Обозначим вектор QQ через 6xi(t). Относительно вектора вариаций можно утверждать следующее.

Так как вариация управления начинается в момент т - Ы, то исходная и проварьированная траектория в этой точке будут совпадать:

хО( 80 = х*(г-80- (1.1-47)

Для исходной траектории можно написать

х (т) = х (-80-{- J x{t)dt,

x-St

тогда как для проварьированной траектории

х*(т) = х*(т - 80+ J x*{t)dt.

Отсюда следует, что

~ ~ /.1

8х(0 = х*(т)-хО(т)= J lx*(0-x (OW, (1.1-48)

или

8х(т)= J [f(x*(Ov)-f(xO(OuO(Ol. (1.1-49)

Для возмущения длительностью bt = eht при и 8/0

X (0-х (т)

и

х*(0-х (0,

X* {() х (т).

Поскольку возмущение, по предположению, возникает внутри области непрерывности u{t), то

uW- и'(т).

Так как f-непрерывная функция х и и, то

1(х*(0, v)=~f(xO(x), v)+ ... ,

7(Х (4 U (0) = f(X (T), П0{0)+

где многоточием обозначены члены, стремящиеся к нулю при Повторная подстановка дает

8х(х)= j[f{x{r),v) -1{хЦ1) и^{г))]Ш+ (1.1-50)

где многоточием заменены бесконечно малые второго порядка по сравнению с е. Так как функции под знаком интеграла не зависят от времени,то

8х(т)=е[Г(хО(х), v)-f(xO(T), иО(т)]Д/+ ... . (1.1-51)

Приращение оптимальной траектории в момент t можно записать в виде

8х(т) = еДх(т) + ... . (1.1-52)

Это приращение будет распространяться вдоль траектории (рис. 1.1-5) и в произвольный момент t при (т</) примет значение бхС^) (точка Q на рис. 1.1-5). Изменение, вносимое возмущением в конечной точке (конечном состоянии), представляет особый интерес.

В связи с этим рассмотрим прежде всего векторную величину

8х(П = еДх(Г)+ .... (1.1-53)

предполагая, что внутри интервала r<t<T сохраняется оптимальное управление u(f). Д-я определения вариации Дх(т) при известном приращении Дх(т) требуется, взяв в качестве начального условия Дх(т), решить в интервале времени x<i<T линеаризованное дифференциальное уравнение

йЛх(0 af(x. U)

Дх(0, (1.1-54)

к = к

соответствующее первому члену разложения в ряд Тэйлора выражения (1.1-7). Записав соотношение (1.1-54) покоординатно, получим

dLxiJt) dfi(x, и)

dt Zi dxi(t)

Xj(t). (1.1-55)

Векторное дифференциальное уравнение (1.1-54) и соответствующая система дифференциальных уравнений (1.1-55) линейны и однородны. Более того, входящая в эти уравнения матрица получается из матрицы вспомогательной системы дифференциальных уравнений (1.1-9) транспонированием и переменной знака, т. е. эти системы сопряженные. Для решения линейной системы необходимо знать переходную матрицу Ф (t, т) (разд. 6, ч. V). Таким образом,

Дх(0 = [Ф^(, )] Дх(т), (1.1-56)

и по теореме о сопряженных системах (разд б, ч. V)

0 (О = [фт {t, т)]-1 0 (т). (1.1-57)

Для приращения в конечный момент времени получим

Дх(Г) = Ф(Г, т)Дх(т). (1.1-58)

Если система находится под воздействием нескольких (например, К) независимых непересекающихся возмущений в области непрерывности управления u(t), то приращение в конечный момент времени

Дх(Г)= S Ф(Г, т,)Дх(т,). (1.1-59)

В добавление к эффекту, вызванному варьированием оптимального управления, рассмотрим влияние изменения конечного момента времени бГ=еАГ, где приращение ДГ необязательно мало и может быть как положительным, так и отрицательным при условии, что е мало.

Положив u*(t)==u (t), найдем, что за счет изменения конечного момента времени смещение

74-гг

8х(Г)= j f{x*{t), u4t))dL (1.1-60)

При £ -5- О x*{i)->- х (t), и мы получим

8x(r) = sf(x (n. u>{T))T+ ...=г^х{Т)+ ... (1.1-61)

или

Дх(Г) = Пх (Г), иО(Г))ДГ. (1.1-62)

Из соотношений (1.1-51), (1.1-59) и (1.1-62) находим, что при одновременном действии всех факторов

Дх(Г)=7(х (П иЦТ))АТ -f S Ф(7, Ч)1Н^{Ч) V,)-

ft = 1

-Пх(т,), и'(т,))]Д4. (1.1-63)

Вектор Дх(Г) не зависит от г, но зависит от т^, v, At и ДГ. Пусть 7-множество этих переменных, а Дх обозначает зависимость приращения Дх(Г) на множестве 7. Если имеется несколько таких множеств, например

Т' = {Ч, V и' ДГ},

Т^ = {т„ V Д4 ДГК (1.1-64)

то в качестве 7 принимается их линейная комбинация

IY + IY + ... = {т„ v XД4 +

+ 1 Ай + XДГ + X ДГ + ... }

с коэффициентами X > О, X > О, ... . Так как Дх (Г) является линейной функцией величин, составляющих множество 7, то

Дх = X Дх., + X Дх., + .... (1.1-65)

Перенесем начало вектора Ах-, в конечную точку х(Т). Для всех возможных значений у, полученных описанным выше способом, совокупность векторов Дх., образует множество Кт, которое является выпуклым конусом. (Множество Кт называется выпуклым конусом, если 1) для любой точки М множества Кт, отличной от вершины Рт, радиус РтМ целиком содержится в этом множестве и 2) отрезок М1М2, соединяющий произвольные точки Ml и М2 множества, принадлежит этому множеству.) Из того, что Дх и Дхпринадлежит множеству Кт и

X Дх., -f X Дх = ДХх'., + х -, , (1.1 -66)

следует, что ДХх'-, + г-, также содержится в этом множестве и поэтому Кт действительно является выпуклым конусом с вершиной х(Т). Конус Кт называется конусом достижимости (рис. 1.1-6). Разумеется, конус Кт не может заполнять всего

векторного пространства состояний. Это следует из того, что точки, расположенные ниже оптимальной траектории, недостижимы. Поэтому через вершину Т можно провести гиперплоскость Г таким образом, что конус Кт целиком будет расположен в одном из полупространств, определяемы.х этой плоскостью (в общем случае возможно существование нескольких пло-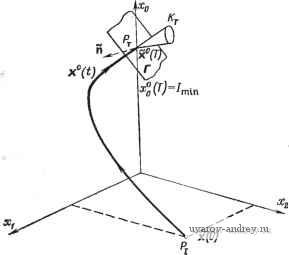

Рис. 1.1-6. Конус достижимости.

скостей Г). Проведем теперь через точку Рт направленную вниз нормаль птк плоскости Г. Для любого вектора Ах е/(т

/г?Дх(Г)<0.

(1.1-67)

Используя это соотношение, нетрудно получить принцип максимума; остается только показать, что для любого вектора vi(t), исходящего из точки х (т),

11) Т(0Ф( )w(t) = ;i50T()w(T) = const (t>z). (1.1-68)

Действительно, подставляя транспонированное выражение (1.1-57)

(1.1-69)

в левую часть соотношения (1.1-68), получим правую часть этого равенства.

с помощью неравенства (1.1-Ь7), относящегося к нормали, принцип максимума можно доказать следующим образом.

Пусть управление u(t) проварьировано в точке непрерывности та=т. Этому случаю отвечает множество

7 = {т, V, и > О, ДГ = 0}.

Отсюда, принимая во внимание только второй член в выражении (1.1-63) для Ах(Т), получим в случае единичной вариации

Дх(Г) = Ф(Г, T)[f(x(T), V)-

-7(х (т), и (т)]Д^ = ф(Г, т)д7(т)й^. (1.1-70)

Подставляя это соотношение в выражения (1.1-67), будем иметь

Л(Г, т)дТ(т)Д^<0. (1.1-71)

Исходя из решения вспомогательной системы дифференциальных уравнений, принимающего в конечный момент времени Т значение

(Г) = 1Гу, (1.1-72)

перепишем неравенство (1.1-71) в виде

отТ)Ф{Т, r)Ai{T)U<0. (1.1-73)

Полагая, кроме того, в выражении (1.1-68) (т) = Д|(т), получим

ф (Т, т) дТ(т) = от ()д7(т),

откуда следует, что неравенство (1.1-73) можно записать в виде

ят()д7()д^0. (1.1-74)

По условию Д^ > О, поэтому

ф'(т)Д?(т)<0, (1.1-75)

или

°T()f(xO(T), v)-f(X (T), U (x))] <0.

По определению гамильтониана, последнее соотношение можно записать в виде неравенства

ф l (т), X (т), vj < Н, \Г (-). х (х), и (т)], (1.1-76)

которое выполняется для произвольной точки непрерывности та=т. Отсюда следует справедливость принципа максимума в рассматриваемом случае.

Предположим теперь, что конечный момент времени претерпевает изменение:

Г = {О, и . О, ДГ).

Учитывая только первый член /S.x(T) в соотношении (1.1-60), получим

nffixЧT),uЧT))T <0, (1.1-77)

или, как следует из выражения (1.1-72),

т(7)7(х0 (Г) и (Г)) ДГ < О, (1.1-78)

Яф(о(Г), х (Г), и (Г))ДГ<0. (1.1-79)

По условию АГ может быть как положительным, так и отрицательным, поэтому приведенное соотношение выполняется при единственном условии

Н^С^{Т), х (Г), и (Г)) = О, (1.1-80)

которое означает, что в конце траектории гамильтониан равен нулю.

Используя равенство

dH дН dx , - du /1 1 й1\

aip ах

можно показать, что в любой другой точке оптимальной траек-тории гамильтониан также обращается в нуль. Из канонических дифференциальных уравнений (1.1-12) следует, что сумма первых двух слагаемых равна нулю и, следовательно.

dH ,дН du

dt au dt

(1.1-82)

Внутри множества V необходимое условие максимума Н, состоит в том, чтобы дНди = 0. Отсюда следует равенство

dHJdt = 0. Если максимум достигается только на

замыкании области управления U, то равенство дН(1д\х = О не будет выполняться. В этих случаях, как пра-

вило, функция u() является постоянной, следовательно,

dwjdt = О и опять dHjdt = 0. Если ни одно из этих условий

не удовлетворяется, можно показать, что векторы dH/du и du/dt взаимно ортогональны и, следовательно, производная

dJfldt всегда равна нулю. Таким образом,

max Яф (t), X (t), u (t) = Щ ( {t), x (/)) = 0,

0<t<T (1.1-83)

всюду вдоль оптимальной траектории. Наконец, из равенства (1.1-72) и условия ПГ(,<0 получим, что

Кроме того, вектор-функция f не зависит от и, как следует из выражения (1.1-13),

Ф8(0 = 0, 0<t<T,

§(0 = to(r) = const<0, Q<t<T.

Иллюстрация принципа максимума. Напомним, что вектор

производной x(t) совпадает с вектором скорости точки x(t) и, следовательно, коллинеарен касательной к траектории. Вектор же1]) (7) ортогонален к касательной и коллинеарен вектору нормали. Действительно, из уравнения (1.1-54), которое справедливо для любого вектора Ах, принадлежащего касательной плоскости к рассматриваемой траектории, и соотношений (1.1-56). (1.1-57) следует, что

(0) Дх(0) = ()дх() = ф'Т(7)Дх(Г) = const. (1.1-84)

Выберем теперь какой-нибудь ненулевой вектор (0), ортогональный к касательной плоскости в точке х(0), т. е. коллинеар-нын нормали nj = n(x (0)). Так как вектор Ах(0) лежит в касательной плоскости, константа в уравнении (1.1-84) равна О и, следовательно, вектор ф (t) ортогонален к касательной плоскости всюду вдоль траектории (О <t < Т) и коллинеарен нормали. Отсюда, а также из условия перпендикулярности касательной и нормали вытекает, что для автономных систем

от~ /7 (,j,o X , и ) = 0; € 10. П

Из условия трансверсальности следует, что оптимальная траектория исходит из начального многообразия (или входит

в множество цели) таким образом, что вектор я]), отвечающий расширенному вектору ф, ортогонален к касательной плоскости начального (или конечного) многообразия (рис. 1.1-4).

1.2. ПРИНЦИП МИНИМУМА ПОНТРЯГИНА

В последнее время принцип оптимальности получил широкое распространение в форме принципа минимума [5*]; преимущества такого подхода состоят в его более тесной связи с вариационным исчислением, принципом Гамильтона в механике и динамическим программированием Беллмана.

При формулировке этого принципа используется вектор вспомогательных переменных р=[ри Рг, .. , PnV, определяемый соотношением

p = ij,= X. (1.2-1)

Кроме того,

Ро = -фо, (1-2-2)

где Р(,>0 (обычно Ро=1)- Таким образом,

Р = -*. (1.2-3)

В этом случае гамильтониан или функция состояния, введенная Понтрягиным,

Hp = Hp (р, X, U, t) = р-Ч{х, U, t), (1.2-4)

и, следовательно.

Общий вид записи канонических дифференциальных уравнений и их векторных эквивалентов остается без изменений:

~ дНр ~ X =- = f (Х, U, t), dp

(1.2-6)

~ - р

Если ро > О, то можно положить Ро() -1- в этом случае достаточно ограничиться 2п каноническими дифференциальными уравнениями или их векторным эквивалентом