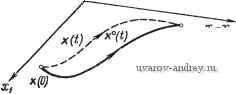Также предполагается, что функция f=f(x, и) непрерывна и имеет непрерывные частные производные по Хг.

Дадим следующее определение отимального управления. В начальный момент 4==о=0 система находится в состоянии х(0). С помощью допустимого управления \i(t) система должна быть переведена в заданное состояние х(Т) в конечный момент времени tf=T, где время Т может быть как закреплено, так и свободно. Допустимое управление u(t) называется оптимальным, если функционал

/-=[/o(xW, и(0)Л (1.1-3)

представляющий характеристику системы (так называемый функционал стоимости), принимает наименьшее возможное зна-

Рис. 1.1-2. Оптимальное управление в пространстве состояний размерности п-2.

чение. Предполагается, что подынтегральное выражение fo, называемое целевой функцией, удовлетворяет условиям гладкости, принятым выше относительно составляющих /г (f=l, 2, ..., п). (Заметим, что наиболее часто рассматривается целевая функция fo==l, для которой /=7\ В этом случае управление оптимально, если оно приводит к минимальному конечному времени Т.) Траектория x(t) = x(t), порождаемая оптимальным управлением и(0 = *(0. называется оптимальной траекторией. Эта траектория является решением векторного дифференциального уравнения (1.1-1), в правой части которого стоит оптимальное управление и (О- Управление и (t) и траектория xf/), удовлетворяющие необходимым условиям оптимальности, называются соответственно экстремальным управлением и экстремальной траекторией. Любое оптимальное управление (траектория) является также экстремальным, так как оно удовлетворяет необходимому условию. Обратное утверждение в общем случае неверно: чтобы экстремальное управление (траектория) было в то же время и оптимальным, оно должно также удовлетворять достаточным условиям.

Так как рассматриваемые системы по предположению автономны, а состояния х(0), х(Т) фиксированы, то обсуждаемая

проблема является задачей оптимального управления автономной системой с закрепленными концами (рис. 1.1-2).

Задачу оптимального управления можно сформулировать также в несколько ином виде. Добавим еще одну переменную состояния, определяемую с помощью интеграла:

о(0= 1/о(х(), u())rf, (1.1-4)

о

где /о-целевая функция из выражения (1.1-3) и 0<т</<Г. Очевидно, что

Хо(0) = 0 и Хе(Г) = /. (1.1-5)

Дифференцируя, получим

о(0=/о(х(/), u(0)=/o(x, U). (1.1-6)

Введем теперь /г+1-мерные векторы; пусть х = fxo, xj, f == = /о, f] и, следовательно, X E +,f Е +. Таким образом, как следует из выражений (1.1-1) и (1.1-6), векторное уравнение состояния можно записать в виде

х = ?(х, U). (1.1-7)

Управление является оптимальным, если составляющая Хо принимает в момент времени tK=T наименьшее возможное значение, т. е. Хо(Т) = тт (рис. 1.1-3).

В соответствии с предложенным Понтрягиным методом [1, 112*] введем вспомогательные переменные фг=фг(0 (i=0, 1, ..., п). Для этого рассмотрим линейную и однородную вспомогательную систему дифференциальных уравнений

. J (=0.1,..., /г), (1.1-8)

в которой частные производные должны быть определены вдоль оптимальной траектории х . В матричных обозначениях дифференциальное уравнение относительно вспомогательных переменных примет вид

J. (1.1-9)

Вспомогательный вектор г];С/) определен только вдоль оптимальной траектории xit). Заметим, что уравнение (1.1-9) соответствует уравнению Эйлера -Лагранжа в вариационном исчислении. Построим теперь гамильтониан или, другими словами,

введенную Понтрягиным функцию состояния

к^ = Нр{\, к, и)=Ч(х, и)= 2 Фг/Дх, U) (1.1-10)

i = 0

или

Яф = ( Р, X. U) = f (X, U) 15 = ДЛ(х, и)фу. (1.1-11)

Таким образом, гамильтониан является скалярной функцией 2п-\-1+г переменных. Из выражения (1.1-10) [или (1.1-11)],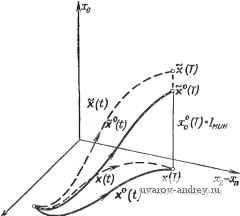

Рис. 1.1-3. Оптимальное управление в пространстве состояний размерности

п+1=3.

Принимая во внимание соотношения (1-1-1) и (1.1-9), найдем, что

или

= 2 = - (/=0,1, ...,/г). (1.1-13)

При этом u=u и х=х'.

Написанные выше два множества рассматриваемых совместно систем уравнений называются каноническими уравне-

(1.1-12)

ниями Гамильтона. Для заданных ф и х и для uU обозначим максимум (точную верхнюю грань) значений функции

через Ж^.(% х):

ЖД, х) = 8ирЯ^(Ф, X, U). (1.1-14)

Согласно принципу максимума [112*], для автономной системы и задачи с закрепленными концами необходимое условие оптимальности управления u(t) и траектории (t), для которых величина Хо(Т)=1 принимает наименьшее возможное значение, состоит в суш;ествовании непрерывной ненулевой вектор-функции (t), задаваемой решением вспомогательной системы и такой, что

Л'( (0. хО(0, иО(0) = Жф(Ф°(0. хО(0) = 0, (1.1-15)

т. е. гамильтониан достигает максимального значения, которое равно нулю; кроме того,

o(0 = const<0 (1.1-16)

для любого t, 0<<Г (часто в качестве ф можно выбрать значение ф^ = - 1).

Принцип максимума для неавтономных систем. Для неавтономной системы с закрепленными концами х(0) и (Т) уравнение состояния имеет вид

k=f(x,u, О- (1-1-17)

Показателем качества служит функционал стоимости, который должен быть минимизирован:

I = If,{x, XX, t)dt. (1.1-18)

о

Вводя дополнительную переменную состояния

Хо=/о(х,и,0, (1-1-19)

запишем расширенное уравнение состояния в виде

х=7(х, U, t). (1.1-20)

Кроме того, предполагается существование и непрерывность всех частных производных (/ = О, 1.....п).

Дифференциальное уравнение для вектора вспомогательных переменных имеет вид

i----; (1.1-21)

в этом случае функция состояния задается формулой

Н^С^, к, и, 0 = f(x, U, i). (1.1-22)

Обозначим

М (, X, t) = sup (ф, X, U, i). (1.1-23)

Согласно принципу максимума для неавтономных систем и задачи с закрепленными начальной и конечной точками [1, 112*], необходимое условие оптимальности хС) и u(t) состоит в существовании непрерывной ненулевой вектор-функции if (t), являющейся решением вспомогательной системы дифференциальных уравнений и такой, что

Яф W (0. X (t) u (t), t) = М.ь (> (О, X {t) t), (1.1-24)

где

Ф2(0 = const <0. (1.1-25)

и

я = ( (0. X (О, о = - J - Ф Ь) (1Л-2б1

для любого t, о < / < тс.

Сведение неавтономной системы к автономной. Неавтономную систему можно свести к автономной [112*], введя еще одну новую переменную

х„-ь,(0 = 1, ,ж(0) = 0. (1.1-27)

В этом случае Xn+\(t)==t и, следовательно, уравнения состояния могут быть записаны в следующем автономном виде:

х,.=/Дх, х„+ U) (/ = 0, 1, .... я), (1.1-28) л; +1 = 1.

Для такой системы вспомогательные дифференциальные уравнения имеют вид

= -%Ь (=0.1,.... ) (1.1-29

и

п

Последнее уравнение можно переписать следующим образом:

Составим теперьгамильтониан системы (1.1-28)

X, х„+ U) = 2 фу/Дх, х„+ U) -f ф„+ (1.1-31)

или

Я;(% ф„+ X, л и) = Яф(Ч), X, t, и)-Ьф + (1.1-32)

где, как следует из равенства (1.1-22), Нф есть гамильтониан неавтономной системы.

В соответствии с принципом максимума для автономных систем можно написать

/(>, Vn+u х , и vf>) = M%(i\ ф^+ь х , 0=0, (1.1-33)

где

и, как следует из выражения (1.1-32), мы действительно получим

Н^{\ х\ t, иО)=-ф°+,(0 = Я( , х , t). (1.1-34) Уравнение (1.1-30) приводит к соотношению

fn,.{T)-U.{i)--\%Щ^П^)а. (1.1-35)

t / = 0

Используя условие трансверсальности (1.1-41), можно показать, что (Т) = О, и поэтому

МДо, X , t, и ) = - (О = J У(х)с?т. (1.1-36)

Следовательно, принцип максимума для неавтономных систем можно сформулировать исходя из принципа максимума для автономных систем.

Задачи с закрепленным временем. При формулировке принципа максимума предполагалось, что значение конечного момента времени Т заранее не определено. Если время Т задано, то число переменных можно уменьшить на единицу. В этом случае для неавтономных систем принцип максимума может быть сформулирован в следующем виде: в задаче с закрепленным временем и для неавтономных систем необходимое условие оптимальности хС), иС) состоит в существовании такого ненулевого решения W> (t) вспомогательной системы дифференциальных уравнений, что

Щ (ф (О, X (О, и (О, О = Щ (0. X (О t) (1.1-37)

и

g(0 = const<0 (1.1-38)

для любого t, 0<i<T.

Благодаря тому что время Т задано, число условий в приведенной формулировке принципа максимума уменьшается на одно.

Для автономных систем условия оптимальности можно определить аналогично, однако в отличие от рассмотренного случая эти условия не будут явно зависеть от времени t.

Условия трансверсальности. Приведенные выше теоремы применяются в тех задачах, когда все координаты начального и конечного состояний, кроме Хо(Т), заданы заранее. Во многих случаях для начального и (или) конечного состояний желательно иметь несколько свободных координат. При этом должны быть выполнены так называемые условия трансверсальности.

Допустим теперь, что конечное время Т свободно. В этом разделе подробно рассмотрим тот случай, когда некоторые (например, k=n - т) или все координаты состояния хСГ) автономной системы свободны. (Аналогичные соотношения могут быть получены также для начального момента времени.)

В п-мерном евклидовом пространстве Е' все т ограничений на вектор состояния х(Г) задаются т соотношениями

/гДх) = 0 (/-1, ...,т), (1.1-39)

каждое из которых определяет некоторую гиперповерхность. В дальнейшем будем предполагать, что О^т^п. Гиперповерхности назовем гладкими, если все элементы dhi

{1=1, ... , т; У=1, .... п)

4 или

порядка пхт или тхп соответственно непрерывны и не равны нулю.

Множество всех векторов х ef , удовлетворяющих одновременно этим условиям, называется (п - т)-мерным гладким многообразием в пространстве Е' при условии линейной независимости векторов

grauh, ii = \.....т). (1.1-40)

Таким образом, матрица dh/dx имеет максимально возможный ранг т.

. Пусть теперь С -гладкое (п--т)-мерное многообразие (множество) в пространстве и х е С. Кроме того, обозначим через Ti касательную гиперплоскость к t-й гиперповерхности, задаваемой соотношением (1.1-39), в точке х (i=l, ..., т). Пересечение Тс касательных плоскостей Tt назовем касательной плоскостью многообразия С в точке х. (Для матрицы максимального ранга найдется только одна такая касательная плоскость.) Размерность касательной плоскости равна п - т. Произвольный (п - ш)-мерный вектор в касательной плоскости Тс, исходящий из точки X, называется касательным вектором многообразия С в точке X (или, если п -т = 1, кривой С).

Пусть х(Т) е С, где С - гладкое (п - т)-мерное заданное многообразие (множество цели) и т - заданная величина. Система должна быть переведена из начального состояния х(0) в конечное состояние х(Т)С таким образом, чтобы минимизировать заданный функционал стоимости (рис. 1.1-4). Из необходимого условия Hw = 0 следует, что вдоль оптимальной траек^; тории, включая обе граничные точки, (п-Ы)-мерные векторы ф

и X должны быть взаимно ортогональны.

Пусть хс - некоторая точка, принадлежащая многообразию С, а Гс -касательная плоскость этого многообразия в точке хс. Предположим, что для автономной системы решение оптимальной задачи определяется вектор-функциями ф' (t), x°(t),

(t). Говорят, что вектор-функцияli? (t) удовлетворяет условию трансверсальности в точке Хс = х(7 ), если вектор (Т) ортогонален касательной плоскости Гс ,Из условия ортогональности можно определить {п - т) составляющих вектора i (Т). Условие трансверсальности также выполняется, если вектор (Т) ортогонален любому вектору v Тс,п, т. е.

фОГ(7)у = 0. (1.1-41)

Для касательной плоскости Тс, размерности п - т условия трансверсальности позволяют, располагая п-т свободными координатами вектора v, получить систему п - т соотношений

для определения вектора ijj (Т). Добавляя к ней заданные т ограничений на координаты вектора хСГ), придем к полной системе п соотношений для момента времени Т. Эти условия обра-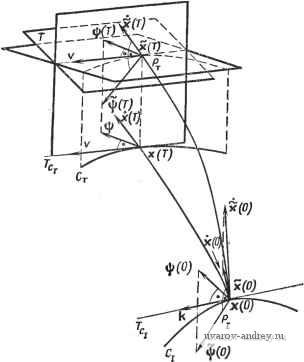

Рис. 1.1-4. Геометрическая интерпретация условия трансверсальности и равенства Нф=0.

зуют достаточную для решения поставленной задачи систему соотношений. Действительно, вектор v удовлетворяет т + 1 уравнениям

v = 0.

X = х (Г)

(1.1-42)

Эти уравнения представляют собой линейные комбинации п - т свободных координат вектора V, и могут быть решены относительно т+1 координаты Vj (/ = 0, 1, 2, ..., т). В результате в уравнениях (1.1-41) должны исчезнуть комбинации п - т свободных координат, и мы получим п - т уравнений для определения п - т составляющих вектора вспомогательных перемен-

ных i (Т). Следует иметь в виду, что величина ijg (Т) здесь не рассматривается и условия трансверсальности определены для вектора ijJ , а не для вектора ijJ .

Можно также показать, что при наличии некоторого числа свободных координат в начальном состоянии условие трансверсальности задается равенством

ii5 t(0)k = 0, (1.1-43)

где к - вектор, принадлежащий (п - т)-мерной касательной плоскости Tcj, т. е. к е Tcf. При этом вектор к определяется уравнениями

к = 0. (1.1-44)

йе-0, -

X = х (0)

Сформулируем теперь принцип максимума для автономных систем и задачи с подвижными концами. В этом случае необходимое условие оптимальности x(t) и u(t) состоит в существовании ненулевой непрерывной вектор-функции °(t), которая является решением вспомогательной системы дифференциальных уравнений и удовлетворяет условиям принципа максимума для автономных систем и задачи с закрепленными концами и, кроме того, условию трансверсальности.

Дополнительные замечания. Приведенные выше теоремы устанавливают необходимые условия оптимальности. Если существует какое-либо оптимальное управление, оно должно удовлетворять соответствующим данной задаче необходимым условиям. Однако обратное утверждение не имеет места, т. е. выполнимость условий принципа максимума указывает только на существование допустимого экстремального управления и не гарантирует, что это управление в то же время является оптимальным.

Наиболее просто достаточное условие оптимальности управления можно сформулировать следующим образом: если среди всех экстремальных управлений u°(t), удовлетворяющих необходимым условиям, найдется управление и (О, для которого минимизируемый функционал принимает наименьшее возможное значение

/(u-(0)>/(u (0), (1-1-45)

то управление и СО оптимально.

Вопросы существования и единственности такого управления занимают одно из центральных мест в теории оптимального управления. Для практических применений, как правило, достаточно установить существование хотя бы одного оптимального решения.