1. Ограничение:

i 2п + 1

п = 0

2. Зона чувствительности:

Х' = /С,

3. Кубическая функция:

4. Идеальное двухпозициоиное реле:

5. Идеальное трехпозиционное реле:

б- Трехпозиционное реле с гистерезисом:

7. Двухпозиционное реле с гистерезисом:

п = 0

4 6. ПРИБЛИЖЕННАЯ КОМБИНИРОВАННАЯ ЛИНЕАРИЗАЦИЯ

Шридхар [12] распространил метод приближенных дуальных описывающих функций (разд. 4.3) на комбинированную линеаризацию. Входной сигнал нелинейного элемента состоит из сину-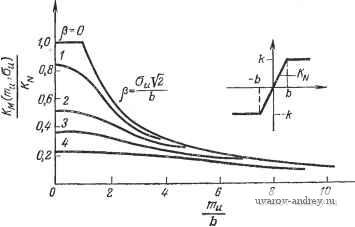

Рис. 4.6-1. Приближенная комбинированная функция для ограничителя.

соидальной составляющей В sin at и шума nu(t) с нормальным распределением:

u{t)== В sin (at+ nu{i). (4.6-1)

Допустим, что граница низких частот шума превышает частоту (й/2я на один порядок. В этом случае синусоидальную составляющую можно считать постоянной и В sin at можно заменить на Ши.

u(t)mu + nu(t). (4.6-2)

Математическое ожидание выходной переменной равно

о(/ . I g{mu+nt))p(u)du.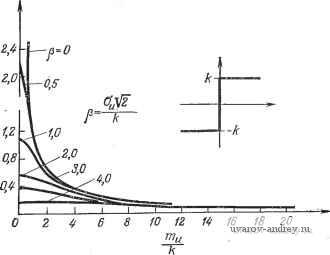

Рис. 4.6-2. Приближенная комбинированная функция для идеального двухпозиционного реле.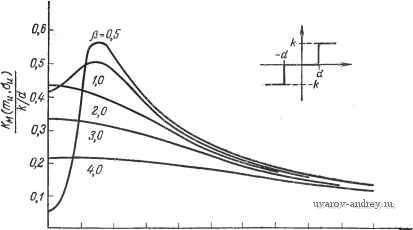

О 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0

Рис. 4.6-3. Приближенная комбинированная функция для идеального трехпозиционного реле.

а приближенный комбинированный коэффициент усиления равен

К (т а =

Таким образом, можно использовать формулы статистической линеаризации из гл. 3 данной части.

Графики приближенных комбинированных описывающих функций для ограничителя и идеальных двухпозиционного и трехпозиционного реле приведены на рис. 4.6-1-4.6-3.

ЛИТЕРАТУРА

1. West J. С, Douce J. L.. Livesley R. K. The Dual Input Describing Function and Its Use in the Analysis of Nonlinear Feedback Systems, Proc. lEE. 1956, 103, Pt. B, pp. 463-474.

2. Boyer R. C. Sinusoidal Signal Stabilization. MS Thesis, Durdue University, Lafayette, 1960.

3. Казаков И. E. Некоторые вопросы теории статистической линеаризации и ее приложений. Труды i Конгресса ИФАК, Москва, 1960.

4. Sridhar R. Signal Stabilization of a Control System with Random Inputs. Ph. D. Thesis. Durdue University. Lafayette. Ind. 1960.

5. Amsler B. E.. Gorozdos E. E. On the Analysis of Bistable Control Systems, IRE Trans. Autom. Control. 1959, AC-4.

6. Bennett W. R. New Results in the Calculation of Modulation Products, EST J.. 1933, 12, pp. 228-243.

7. Bonenn Z. Stability of Forced Oscillations in Nonlinear Feedback Systems. IRE Trans. Autom. Control, 1958, AC-3, pp. 109-111.

8. Bonenn Z. Relative Stability of Oscillations in Nonlinear Control System, Proc. IFAC, Basel, Switzerland. 1963, pp. 214/1-4.

9. Douce J. L. King R. E. Instability of a Nonlinear Conditionally Stable System Subjected to a Sinusoidal Input, Trans. AIEE, 1959. 78, Pt. II. pp. 665-670.

10. Douce J. L. Discussion of a paper by Ogata, Trans. ASME. 1958, 80, № 8, p. 1808.

11. Elgerd O. I. High-Frequency Signal Injection: A Means of Changing the Transfer Characteristics of Nonlinear Elements, Wescon, 1962.

12. Gibson J. E., Sridhar R. A New Dual-Input Describing Function and an Application to the Stability of Forced Oscillations. Trans. AIEE. Pt. ii, 1963, 82, pp. 65-70.

13. Huey R. M., Pawloff O., Glucharoff T. Extension of the Dual-Input Describing-Function Technique to System Containing Reactive Nonlinearity, J. lEE. 1960 C-107, pp. 334-341.

14. Kalb R. M., Bennett W. R. Ferromagnetic Distortion of a Two-Frequency Wave. EST J.. 1935. 14, pp. 322-359.

15. Ludeke C. A. The Generation and Extinction of Subharmonics, Proc. Symp. Nonlinear Circuit Analysis II, Polytechnic Institute of Brooklyn, N.Y., 1953.

16. Oldenburger R., Boyer R. C. Effects of Extra Sinusoidal Inputs to Nonlinear Systems. Trans. ASME J. Basic. Eng.. 1962. £-84, pp. 559-570.

17. Oldenburger R., Nicholls R. Stability of Subharmonic Oscillations in Nonlinear Systems. Proc. JACC Minneapolis, 1963, pp. 675-680.

18. Rice S. O. Mathematical Analysis of Random Noise, EST J.. 1945, 24, Pt. IV, pp. 109-156.

19. West J. C. Douce J. L. The Mechanism of Sub-Harmonic Generation in a Feedback System. J. lEE. 1955. B-102, pp. 569-574.

20. Atherton D. P., Turnbull G. F., Qelb A., Van der Velde W. E. Discussion of the Double Input Describing Function (DIDF) for Unrelated Sinusoidal Signals, IEEE Trans. Autom. Control. 1964, AC-9, № 2, pp. 197-198.

21 Furman Q. Q. Removing the Noise from the Quantization Process by Dit- hering: Linearization, RAND iHem. RM-3271-RP, 1963, pp. 1-40.

22 Gelb A. The Dynamic Input-Output Analysis of Limit Cycling Control Systems, Proc. JACC, New York University, N. Y., 1962, pp. 9.3/1-9.3/11.

23 Qelb A., Blaschke T. C. Design for Adaptive Roll Control of a iVlissile, J. Aeron. Astronautics, 1962, 9, № 4, pp. 99-105.

24 Qelb A., Van der Velde W. E. On Limit Cycling Control Systems, IEEE Trans. Autom. Control, 1963, AC-8, № 2, pp. 142-157.

25. Королев H. A. Импульсная стабилизация релейных систем регулирования. Автоматика и телемеханика, 1958,18, № 5, стр. 435-446.

26 Li Y. Т., Van der Velde W. E. Philosophy of Nonlinear Adaptive Systems, Proc. First IF AC Congr., iVloscow, 1960, Butterworth Scientific Publications, London, 1961.

27. Loeb J. M. A General Linearizing Process for Nonlinear Control Systems, Manual and Automatic Control, Butterworth Scientific Publication, London, 1952, pp. 274-284.

28. Lozier J. C. Carrier-Controlled Relay Servos, Elec. Eng.. 1950, 69, pp. 1052-1056.

29. Minorsky N. On Asynchronous Action, J. Franklin Inst., 1955, 59, pp. 209-219.

30. Naslin P. A Simplified Theory of Feedback Control Systems, Part 12, Process Control and Automation. 1959, 6, № 6, pp. 273 277.

31. Oldenburger R. Signal Stabilization of a Control System, Trans. ASME, 1957, 79, pp. 1869-1872.

32. Oldenburger R., Liu C. C. Signal Stabilization of a Control System, Trans. AIEE, 1959, 78, Pt. II, pp. 96-100.

33. Oldenburger R.. Nakada T. Signal Stabilization of Selfoscillating Systems, IRE Trans. Autom. Control, 1961, AC-6, № 3, pp. 319-325.

34. Shuck O. H. Honeywells History and Philosophy in the Adaptive Control Field, Tech. Rept., Wright Patterson Air Force Base, Ohio, 1959.

35. Rao P. A., Janakiraman P. A. Dual Input Discrete Describing Function, IEEE Trans. Autom. Control. 1969. AC-14, pp. 427-429.

36. Rao M. V. C, Rao P. V. A Comment on the Discrete Describing Function Method, IEEE Trans. Autom. Control. 1970, AC-15, pp. 270-271.

37. Rao M. V. C, Rao P. V. A Note on the Dual Input Discrete Describing Function, IEEE Trans. Autom. Control, 1970. AC-15, pp. 375-376.

38. Shinners S. M. Dual Input Describing Functions, Control Engineering, 1971, pp. 53-55.

Часть III. ОПТИМАЛЬНЫЕ СИСТЕМЫ

Интенсивное развитие техники автоматического управления и регулирования во время второй мировой войны далее отразилось на автоматизации промышленности, уровне вычислительной техники и достижениях в освоении космического пространства. В настоящее время в различных областях практики значительно возросли потребности в использовании систем оптимального управления для разных критериев оптимальности. Понятие оптимальности определяется принятым критерием оптимизации, и система, оптимальная по одному критерию, разумеется, может быть неоптимальной по другому критерию. За характеристику оптимальности обычно принимают некоторый показатель качества; в ряде случаев эту характеристику дополняют, вводя второстепенные показатели. Задача оптимизации, как правило, состоит в отыскании минимума некоторого функционала (общей стоимости или штрафа), реже -в максимизации другого функционала (суммарного результата, эффекта или выигрыша).

Отметим следующие преимущества методов оптимизации:

1. Можно получить математическое решение задачи прямого синтеза по критерию качества.

2. Становится понятным значение предъявляемых к системе теоретических и практических ограничений. В том случае, если имеются противоречивые требования, их легко обнаружить.

3. Сравнительно просто предсказать поведение системы в недалеком будущем или для изменившихся условий.

4. Управление моЖет быть адаптивным. Для этого надо использовать модифицированный критерий оптимальности и изменяющиеся параметры.

5. Нестационарные системы можно оптимизировать, используя вычислительные устройства.

6. Нелинейные системы можно оптимизировать, но в этом случае требуются громоздкие вычисления.

Отметим также некоторые недостатки методов оптимизации.

1. Математическая постановка задачи проектирования достаточно сложна; ее решение может потребовать применения метода проб и ошибок.

2. Только простейшие оптимальные системы можно синтезировать простыми средствами; для более сложных систем неизбежно потребуется использовать аналоговые или цифровые вычислительные устройства.

3. Для сложных, в частности нелинейных, систем алгоритмы оптимизации трудоемки для программирования, время их машинной реализации достаточно велико.

4. Качество оптимальной системы сильно зависит от неточности исходных допущений и от изменения параметров управляемого объекта.

5. Система, оптимальная в некотором смысле, с другой точки зрения может оказаться неоптимальной и даже бесполезной.

Основные принципы оптимизации были развиты в статистической теории фильтрации Винера [148*] и Колмогорова [1, 2, 71*]. Бутон и др. [3] распространили теорию фильтрации и предсказания на нестационарные системы. Исходя из физических соображений, Ньютон и др. [105*] исследовали аналогичные вопросы с учетом ограничений на среднеквадратичные значения переменных. Все эти принципы оптимизации применяются в первую очередь для определения оптимальных переходных и весовых функций линейных систем статистическими методами.

Принципы оптимизации, предложенные Понтрягиным и его коллегами [4-6, 112*], а также Беллманом и др., по существу отличны от перечисленных выше. Один из принципов является развитием и обобщением методов вариационного исчисления, а другой - основан на динамическом программировании. В обоих случаях конечная цель состоит в определении управляющих переменных в функции времени, т. е. в установлении оптимального закона управления. Кроме того, требуется также наметить в общих чертах структуру оптимального управляющего устройства. Независимо от используемого метода расчет оптимальной системы состоит из трех этапов:

1) формирование показателя качества, для которого решается задача оптимизации;

2) определение оптимального закона управления;

3) определение структуры оптимального управляющего устройства.

ЛИТЕРАТУРА

1. Колмогоров А. Н. Интерполирование и экстраполирование стационарных случайных последовательностей. Язе. АН СССР, сер. мат., 1941, № 1, стр. 3-14.

2 Колмогоров А. Н. Стационарные последовательности в гильбертовом пространстве. Бюллетень МГУ, 1941, 2, вып. 6, стр. 1-40.

3. Booton R. С. The Analysis of Nonlinear Control Systems with Random Inputs. Proc. Symposium on Nonlinear Circuit Analysis, II, Brooklyn Polytechnic Institute, 1933, pp. 369-391.

4. Болтянский В. Г., Гамкрелидзе Р. В., Понтрягин Л. С. К теории оптимальных процессов, ДЛЯ СССР, сер. мат., 1958, 22, № 4, стр. 449-474.

5. Понтрягин Л. С. Оптимальные процессы регулирования, Успехи мат. наук, 1959, 14, № 1, стр. 3-20.

6. Болтянский В. Г. Принцип максимума в теории оптимальных процессов, ДАН СССР, 1958, 119,Jsfo б, стр. 1070-1073.

7. Bellman R., Dreyfuss S. Functional Approximations and Dynamic Programming, Mathematical Tables and Other Aids to Computation. 1959, 13, >f2 68.

8 Bellman R., Olicksberg I., Gross O. On the Bang-Bang Control Problem. Quart. Appl. Math.. 1956. 14, pp. 11-18.

9. Баранов A. Ю. Трухаев P. И., Хоменюк В. В. Обоснование метода погружения в вариационных задачах, Автоматика и телемеханика, 1967,28, №7.

10. Berkovitz L. Variational Methods in Problems of Control and Programming. J. Math. Analysis. Appl.. 1961, 3, pp. 145-169.

11 Breakwell J. V., Speyer J. L., Bryson A. E. Optimization and Control of Nonlinear Systems Using the Second Variation, J. SIAM on Control, 1963, Ser. A, I, № 2, pp. 193-223.

12. Desoer C. A. The Bang-Bang Servo Problem Treated by Variational Techniques, Information and Control. 1959, 2, pp. 333-348.

13. Desoer C. A.. Wing J. An Optimal Strategy for a Saturating Sampled-Data System, IRE Trans, on Automatic Control. 1961, AC-6, № 2.

14. Desoer C. A. The Bang-Bang Servo Problem Treated by Variational Techniques, Inform. Control. 1959, 2, pp. 333-348.

15. Dreyfus S. E. Computation Aspects of Variational Problems. J. Math. Analysis Appl., 1961, 3.

16. Dreyfus S. E. Dynamic Programming and the Calculus of Variations. /. Math. Analysis Appl., 1960, 1. № 2, pp. 228-239.

17. Kalman R. E. The Theory of Optimal Control and the Calculus of Variations, в книге Bellman R. (ed.) Mathernatical Optimization Techniques, University of California Press, Berkeley Calif., 1963.

18. Kelley H. J. A Second Variation Test for Singular Extremals AIAA Journ.,

1964, pp. 1380-1382.

19. Кротов В. Ф. Приближенный синтез оптимального управления, Автоматика и телемеханика, 1964, 25, № 11, стр. 1521-1.527.

20. Кротов В. Ф. Методы решения вариационных задач на основе достаточных условий абсолютного минимума, I, II, III, Автоматика и телемеханика. 1962, 23,№ 12; 1963, 24, № 5; 1964, 25, № 7.

21. Leitmann G. Some Variational Problems in Rocket Flight, J. Aerospace Set., 1959, 26, № 9, pp. 58ff.

22. Leitmann G. On a Class of Variational Problems in Rocket Flight. J. Aerospace Sci.. 1959. 26, pp. 58ff.

23. McCann M. J. Introduction to Variational Methods for Optimal Control, Trans, of the Soc. of Instr. Technology, 1961, № 12, pp. 232-237.

24. McShane E. J. On Multipliers for Lagrange Problems, Amer. Journ. of Mathematics, 1939. 61, pp. 809-819.

25. Merriam C. W. Computional Method for Feedback Control Optimization, Information and Control, 1966, 8, pp. 215-232.

26. Островский Г. М., Волин Ю. М., Малкин И. И. Об одном методе решения оптимальных задач с краевыми условиями. Техническая кибернетика,

1965, № 6.

27. Розоноэр Л. И. Вариационный подход к проблеме инвариантности систем автоматического управления, I, II, Автоматика и телемеханика, 1963, 24, № 6-7, стр. 744-756, 861-870.

28. Троицкий В. А. Задача Майера - Больца вариационного исчисления и теория оптимальных систем. Прикладная мат. и мех., 1961, 25, № 4.

29 Троицкий В. А. О вариационных задачах оптимизации процессов управления. Прикладная мат. и мех., 1962, 26, Ш i.

30 Троицкий В. А. Вариационные задачи оптимизации процессов в системах с ограниченными координатами. Прикладная мат. и мех., 1962, 26, № 3.

31. Воробьев Л. М., Воробьева Т. М. Нелинейные преобразования в вариационных задачах. Автоматика и телемеханика, 1962, 27,.jsfe 5.

32 Warga J. Necessary Conditions for Minimum in Relaxed Variational Problems, J. Math. Anal. AppL, 1962, 4, pp. 129-145.

33 Kalman R. Contributions to the Theory of Optimal Control, Bui. Soc. Math. Max.. 1960, 5, pp. 102-119.

34. Kalman R. E. The Theory of Optimal Control and the Calculus ol Variations, в книге Bellman R. (ed) Mathematical Optimization Techniques, University of California Press, Berkeley, Calif., 1963.

35. Merriam III C. W. An Optimization Theory for Feedback Control System Design, Informal. Control, 1960, 3, pp. 32-59.

36. Merriam III C. W. A Class of Optimum Control Systems, J. Franklin Inst, 1959, 267, № 4.

37. Burghart J. H. Suboptimal Linear Regulators for Systems Subject to Parameter Variations, IEEE Trans. Autom. Control, 1969, AC-14, pp. 285-289.

38. Lastman Q. J. An Integral-Equation Function-Space Method for Solving Inequalityconstrained Optimal Control Problems. Int. J. Control, 1970, 12, pp. 511-524.

39. Mohri A. A Computational Method for Optimal Control of a Linear System by Ouad,Taiic Programming, Int. J. Control, 1970, 11, pp. 1021-1039.

1. ПРИНЦИП ПОНТРЯГИНА

В теории систем оптимального управления принцип Понтря-гика занимает особое место [1]. Этот принцип был впервые сформулирован в 1956 г., однако широкое признание он получил только после проведения I Конгресса ИФАК в 1960 г.

В работах Понтрягина и его сотрудников [1-8] понятие оптимальности формулируется в форме принципа максимума.

Особенностью принципа минимума, введенного недавно в работе [5*], является его тесная связь с принципом Гамильтона в механике и с функциональными уравнениями Беллмана в динамическом программировании [37, 8*]. Как и следовало ожидать, применение принципов максимума и минимума приводит к одному и тому же с точностью до знака результату. Фактически эти принципы представляют собой распространение вариационного исчисления на область задач, в которых вектор управления подчинен некоторым ограничениям [5*, 6*, 8*, 9*, 13*, 15* 16*, 19*-22*, 24*, 27*, 31*, 34*, 38*, 41*-44*, 52*, 57*, 59*-61*, 73*, 77*, 85*, 87*, 88*, 90*-97*, 103*, 107*, 112*, 113*. 116*-118*, 127*, 134*-136*, 142*, 143*, 152*]. В данном разделе рассмотрены оба принципа.

Прежде чем приступить к детальному обсуждению, остановимся кратко на обозначениях. Для удобства принятые в вариационном исчислении обозначения целевых функций F заменим в математической теории оптимального управления на /о. Вместо вектора множителей Лагранжа X (t) вариационного исчис-

ления рассмотрим в методе принципа минимума, вектор вспомогательных переменных p(t), которому в принципе максимума отвечает вектор-функцияСО; СО = Р(0=-(0- Следовательно, гамильтониану Я=F-ьXтf вариационного исчисления соответствуют выражения Яр=/о+р'1 в случае принципа минимума и Я15=-fo+lf в случае принципа максимума. Канонические уравнения Гамильтона для всех трех случаев формально совпадают.

1.1. ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА

Принцип'максимума для автономных систем. Сформулируем сначала принцип оптимальности в его первоначальной форме принципа максимума [1]; для простоты будем рассматривать случай автономных систем. Уравнения состояния автономного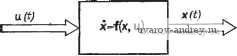

Рис. 1.1-1. Блок-схема автономной системы управления.

управляемого объекта (рис. 1.1-1) задаются обычно векторным дифференциальным уравнением

x = f(x(0, u(0),

или (1.1-1)

x = f(x, u),

где X - -мерный вектор состояния, и - .-мерный вектор управления, f - n-мерная вектор-функция векторных аргументов. Время t не входит явно в уравнение движения; поэтому система (1.1-1) может быть названа автономной.

Исходя из физических соображений, ограничим класс управляющих воздействий иСО кусочно-непрерывными управлениями с ограниченными компонентами. Таким образом, предполагается, что

u{i)U,Yi, (1.1-2)

где область управления U представляет собой замкнутое и ограниченное (компактное) подпространство г-мерного евклидова пространства f, не зависящее от х и Любое такое управление иСО 6 называется допустимым Кроме того, хСО где - евклидово пространство размерности п.