(Это выражение справедливо и при т = Vs-) Таким образом, инфинитезимальная частотная реакция имеет вид

G (уо)) = 4 КмВЮ, ijw) О2 (уш).

Если траектория О, (уа))02(уа)) линейной части не пересекает отрицательную действительную полуось, то О (ум) не будет содержать точку -1, и никакие устойчивые вынужденные колебания не возникнут.

Пример 2. Рассмотрим случай при т=1. Если М-В, то

N[{B, ф, 1) = 4/<л,5М2 + со8ф + у8ш2ф)= К^,ВЦ2 + е^).

Траектории инфинитезимальных описывающих функций являются окружностями радиуса KjB с центром JKjB . Так как

то траектории располагаются внутри сектора ±30° относительно положительной действительной полуоси. Таким образом, условие устойчивости вынужденных колебаний состоит в том, что траектория -(/со) G2(/cu), обратная отрицательной частотной реакции линейной части, не заходит в сектор ±30°. Можно показать, что кривая -\IN\, обратная инфинитезимальной описывающей функции, является окружностью, расположенной в секторе ±150°. Другими словами, условие устойчивости вынужденных колебаний состоит в том, что частотная реакция линейных элементов Gj (/со) G2(/cu) не должна попадать в сектор 180° ±30°.

Пример 3. При т = 3 описывающая функция для частоты со (рассматриваемой как субгармоника) имеет вид (см. пример в разд. 4.1)

Al {В, Ж, ф, 3) = 4 (+ cos Зф -f jBM sin Зф) =

= 4 ( + 2? - ВМе-1).

Отсюда следует, что описывающая функция представляет

собой окружность радиуса j/CyvjW с центром/Сд (i52-f2jW2).

Касательная из начала координат к этой кривой дает

Tj = max (arctg + cos Зф) = s WW Экстремум функции равен (ум)тах= ±21° при В/Л1=±/2.

Если фазовый сдвиг диаграммы Найквиста, вычерченной только для линейных элементов, не меньше -159°, то субгармонические колебания не возникают. Напротив, если частотная реакция линейных элементов попадает в сектор ±159°, субгармонические колебания могут возникнуть. Амплитуду и частоту этих колебаний можно определить обычным способом.

Пример 4. Для изучения третьей гармоники основной является описывающая функция N3(8, М, гр, 3), определенная в примере разд. 4.1:

N,{B, М, ф, 3)= 4/Сд,[3(252 + Ж2)-со8ф-у.8шф

м

Траектория является окружностью. В данном случае

- g3

Поскольку 7 не ограничена, условие

NsiB, М, ф, 3)Oi(уЗш)0.2(Зуш) = - 1

удовлетворяется или, другими словами, третья гармоника генерируется всегда.

4.3. АППРОКСИМАЦИЯ ДУАЛЬНЫХ ОПИСЫВАЮЩИХ ФУНКЦИЙ

Определение дуальных описывающих функций является довольно трудной задачей. Бойер [2] разработал метод аппроксимации, достаточно точный, если частота второй составляющей превышает частоту основной составляющей по крайней мере на один порядок (т. е. отношение частот не должно быть целым). Входная переменная имеет вид

и (t) = sin ш/ -f Bs sin 94, (4.3-1)

где Во> sin at - низкочастотная и Вя sin Qt - высокочастотная составляющие при условии (амплитуды В , fig не ограничены). Поскольку £2:>со, низкочастотную составляющую можно считать постоянной в течение любого периода 2n/Q- Приближенная дуальная описывающая функция определяется в четыре этапа.

1. На первом этапе находят эквивалентный коэффициент усиления для постоянной составляющей. Пусть переменная на входе нелинейности записывается в виде

u{t) = U + Bp,sm94, (4.3-2)

а на выходе-в виде

и (t) = Ло + fii sin 9 + Л1 cos + .... (4.3-3)

Коэффициент усиления для постоянной составляющей при этом равен

KAB9.,U). (4.3-4)

Например, для идеального двухпозиционного реле коэффициент усиления Ко равен

Ко(В^, 7) = ?гarcsin

пи Bq

Для ограничения или насыщения он равен

+ -2 + - + ( 2 - О

где tti = arcsin [(& - U)IBs\ и = arcsin [{b + i/)/i5s]. Для зоны чувствительности

Ao (. Щ = Kn - ~Kn 1 + 2 + 77- (cos 2 - cos Kj) +

+:( 2-a,)

где 1 = arcsin [(rf - У)/59] и 2 = arcsin \{d + {/)/59]. Для идеального трехпозиционного реле

/Со (5., 7)=-1(0,3-а,).

где Oi и аг определяются по формулам, записанным выше (если cf=0, выражение совпадает с выражением для идеального двухпозиционного реле).

2. На втором этапе определяют для низкочастотной составляющей переменную на выходе нелинейности. Заменяя составляющую Бш5Шы/ константой U для каждого периода 2я/й, т. е. используя уравнение (4.3-2), составляющую Ло выходного сигнала можно определить для любого периода 2я/£2 как произведение Ко на и. Сглаживание полученной таким образом ступенчатой или квантовой кривой приводит к эквивалентному выходу.

3. Затем определяют измененную нелинейную характеристику Au(U). Ее строят по точкам, пользуясь только низкочастотной составляющей BmSinco/ и эквивалентным выходом (допускается, что высокочастотная составляющая BsinQt изменяет нелинейную характеристику только по отношению к низкочастотной составляющей, тогда как сама она в значительной

степени подавляется элементами типа низкочастотных фильтров в замкнутой цепи). На рис- 4.3-1 приведена измененная нелинейная характеристика Ao(U) для идеального реле, а на рис. 4-3-2-

Рис. 4.3-1. Измененная нелинейная характеристика Ai>{lJ) для идеального

для ограничителя с различными значениями амплитуды (или Вв/Ь), взятой в качестве параметра.

4. Наконец, определяют основную составляющую эквивалентного выхода (например, графическим способом).Далееопи-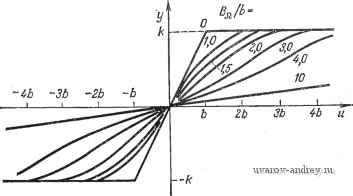

Рис. 4.3-2. Измененная нелинейная характеристика Ao(U) для ограничителя.

сывающая функция Л/(В„, Вв) может быть получена обычным образом. Приближенные дуальные описывающие функции наиболее распространенных нелинейностей приведены на рис. 4.3-3- 4.3-6, С помощью приближенных описывающих функций

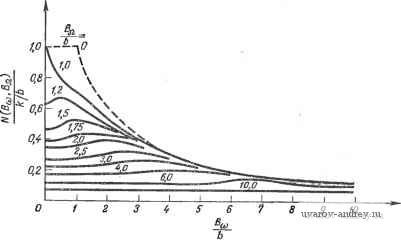Рис. 4.3-3. Приближенная дуальная описывающая функция нелинейности типа

ограничения.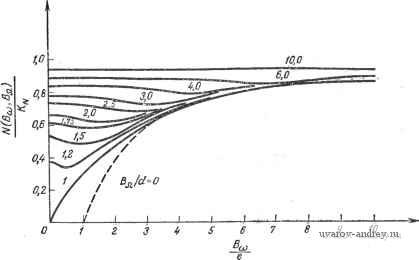

Рлс. 4.3-4. Приближенная дуальная описывающая функция нелинейности типа зоны нечувствительности.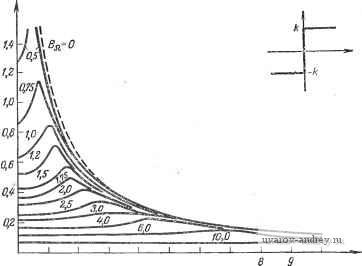

г 3 4 5 6 7

Рис. 4.3-5. Приближенная дуальная описывающая функция нелинейности типа идеального двухпозиционного реле.

0,6 0,4 0,2

= 1.0

с

Рис. 4.3-6. Приближенная дуальная описывающая функция нелинейности типа трехпозиционного реле с зоной нечувствительности.

N{B, Ва) проверка устойчивости может быть сделана обычным способом.

Задача 1. Пусть передаточная функция управляемого объекта системы управления с жесткой обратной связью равна GCs)=5/s( 1+5)2, g управляющее устройство является усилителем с насыщением с Ь - 2, k=4, Kn=2. Доказать существование устойчивого предельного цикла.

Добавить высокочастотную составляющую Вы sin Qt к эталонному входу (которая будет пренебрежимо малой в управляющей переменной из-за подавления ее низкочастотным фильтром) и затем определить величину амплитуды Вв, при которой не возникает генерации предельного цикла.

Задача 2. Заменив усилитель с насыщением в предыдущей задаче на идеальное реле с k=\, показать, что при значениях (0= 1, yV(B ) =0,4 и Bu)=10/jt возникает сходящийся предельный цикл. Доказать, что этот предельный цикл можно устранить, добавляя высокочастотную составляющую с амплитудой

>2.2.

4.4. КОМБИНИРОВАННАЯ ГАРМОНИЧЕСКАЯ И СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ

Этот метод предложен Казаковым [75*, 119*]- Входной сигнал нелинейного элемента может состоять, как уже говорилось в начале данной главы, из гармонической и случайной переменных

v{t) = Bsmii>t + u{t), (4.4-1)

v{t) = Bsm + m (t)-\-n (t). (4.4-2)

В этом случае коэффициенты усиления, определенные с помощью статистической линеаризации, являются периодическими функциями времени, так как даже в случае стационарного стохастического процесса с m = const математическое ожидание сигнала v(t) будет периодической функцией времени. Эквивалентный коэффициент усиления (описывающая функция), найденный с помощью гармонической линеаризации, зависит от статистических данных (математического ожидания и стандартного отклонения), так как имеется стохастическая составляющая- Поэтому предпочитают линеаризовать нелинейное уравнение, заданное нечетной функцией

y{t)g{v(i)), (4.4-3)

С помощью приближенного соотношения

у {t) <ро + В sin iot + Х'В cosoii + й„ (t), . (4.4-4)

где

<Ро = мгпи, (4.4-5)

и первую составляющую можно считать пропорциональной полезной входной составляющей

Комбинированную линеаризацию можно осуществить несколькими способами. Предположим, что случайная составляющая входной переменной изменяется медленно и может рассматриваться как постоянная в течение одного периода.

Прежде всего выполним статистическую линеаризацию

У (О - go (fv °v) + К а (m, о^) Пи (4.4-6)

или, более подробно,

y{t) -go{Ши+Вsinwt, aJ+KAiniu+Bsinwt, cja, (4.4-7)

где mv=mu+В sin at и av = Ou. Благодаря наличию синусоидальной составляющей go и Ка являются периодическими функциями и гармоническая линеаризация возможна. Рассматривая стандартное отклонение Ои как постоянную, разложим функцию go в ряд Фурье и ограничимся первой гармоникой

go {т^+В sin Ы, о„) ~ (В, т„, о„) -f

-f X {В, m , о J Bsinot + r {В, m , о J В cos ot, (4.4-8)

где

<Ро {В, /п„, ° ) = f go {Щь + В sin ш4 о J dwt, о

X (Д ш„, ° ) = J 0 (/и + sin wt, о„) sin №/ dwt,

о

Х'(5, т„, О = J go (/ и + В sin wt, о J cos wt dwt.

в разложении в ряд статистического коэффициента усиления Ка оставляют лишь постоянный член. Из нелинейного выражения для y(t) получаем

К а (/п„ -1- В sin wt, о„) ~ Ха {В, т„, о„) =

= J /Сл (т„ -f 5 sin 10, о„) dwt. (4.4-9)

о

Подставляя выражения (4.4-8) и (4.4-9) в первоначальное уравнение (4.4-7), найдем приближенное соотношение (4.4-4).

Выражение для go и Ка из уравнений (4.4-8) и (4.4-9) можно получить по правилам статистической линеаризации.

К А (т„ -f В sin Ы, о J = [ Kg (/п„ + В sin ш^, о„) -f

go(m -f5sinu), о„)= j g(u +В sin Ы)р (и) du, (4.4-10)

[Ksim +В sin wt, oj-f -f/C(/n -b5sinu) с„)], (4.4-11)

Кs (ni + В sin Ы, o ) = = ± - \ g (tt+5 sin iot) p {и) du-gl (m -f В sin ш^, ojl

U J

(4.4-12)

/Ci, (m -f sin < c ) = (u-mu)g{u+В sin 4>t)p{u)du.

(4.4-13)

Если статическая характеристика нелинейного элемента центрально-симметричная, то

-м и) = = I ё о ( + ° )

(4.4-14)

Статистические коэффициенты усиления %м и %а представляют собой средние значения за период 2я от статистических коэффициентов усиления Км и Ка. Коэффициенты х и х' являются гармоническими коэффициентами усиления функции go, полученной из функции g статистическим осреднением. Наконец, фо является средним значением функции go за период 2п-

Обратная процедура также возможна: выполняя сначала гармоническую, а затем статистическую линеаризацию, придем к тому же результату.

Иногда лучше начинать с записи входного сигнала в комплексной форме

v{t) = m + BeJ + nAt) и записи выражения приближенной линеаризации в виде yii)=% + NBef- + XnJt),

Где описывающая функция

N=N{B, m , a ) = X(fi, /п„, c)+jT{B, 7П„, е„)

зависит не только от амплитуды В, но также от математического ожидания ГПи и стандартного отклонения Ои- Аналогичные рассуждения применимы и к фо, Хм и ха.

Однако комбинированная линеаризация чрезвычайно сложна и поэтому используется довольно редко.

4.5. ОБЗОР ФОРМУЛ КОМБИНИРОВАННОЙ ЛИНЕАРИЗАЦИИ

Приведем некоторые дополнительные формулы комбинированной гармонической и статистической линеаризации для нескольких типичных нелинейностей. При комбинированной линеа-

OA -

Рис. 4.5-1. Графики первых четырех функций D .

Рис. 4.5-2. Графики первых четыре.х функций Еп.

ризации, т. е. при определении % и требуется использование функций

г = 0

Р ( \ - VI S {-W+ \2(r + n)]\ (J\2r - у (2 )! {г + пу. \2J

г = 0

(/г = О, 1, 2, ...), (4.5-2)

где'{ = BI{Y2aa)- Графики первых четырех функций приведены на рис. 4.5-1 и 4.5-2-Введем выражения Xi = 2 oj и = = Л/(/2а„).

Для определения других коэффициентов можно использовать ранее полученные формулы гармонической и статистической линеаризации.