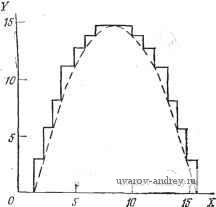Рис. 1.49. График значений выходной переменной.

Опишем эти шаги применительно к проектированию сумматора.

Шаг I. Выбор в качестве входных переменных а, 6 и yfe, в качестве выходных CHS.

Шаг 2. Построение карт Карно для с и s (рис. 1.47).

a1xL

Рис. 1.50. Карта Карно для генератора функции y==smx.

для переменной уЪ; б-для переменной у2: в-для переменной 1; г-для пере-

ЫГЧЙ fin

а .. менной I/O.

s:z-

Х1

t6g\-

У

т

>

~пзу

>

х^

~1тт\-

Isoyy-

Х1

У

?&Г)>-

= 18е)>

Рис. 1.51. Логические схемы для генератора синусоидальной функции на вентилях НЕ-И.

с -для переменной уЪ; б -для переменной 1/2; е - для переменной г/1; г - для переменной ф.

Шаг 3. Запись логических выражений для с и s:

c = dbbk-{-ak s = a®b®k. Шаг 4. Изображение схемы (рис. 1.48).

Описание работы генератора тригонометрической функции y=sinx приведено в табл. 1.7 [7].

На рис. 1.49 изображены значения выходной переменной У~уЗ, у2, у1, уО для входной переменной Х=хЗ, х2, х1, хО, монотонно меняющейся от О до 15.

В данном случае y=f{x). Ясно, что входными переменными являются X, а выходными У. Таким образом, действия, предписываемые шагом 1, выполнены. Далее, согласно шагу 2, для выходной величины требуется построить карту Карно. Эти карты изображены на рис. 1.50. Затем в соответствии с указаниями Шага 3 должны быть записаны следующие логические выражения, определяющие работу проектируемого синусоидального гег

нератора:

у1 = хЫ)+х2х1 -\-х2хО-1-х2х\хО-\-хЗИх\,

уО=;с2д;1 хО + хЗхЫ +~хЗх1хО-{- x2Jd Зсб+хЗдг! хО.

Шаг 4 проектирования предполагает построение схемы, реализующей требуемые функции (рис. 1.51). Для простоты изображения на этом рисунке опущены некоторые связи, например Аа, ВЬ и другие.

1.19. УПРАЖНЕНИЯ

У.1.1. Используя карты Карно, представьте следующие функции в виде разложений по минитермам:

a) HW, X. У, 2)=У2ч-Х(Уч-У2); б) f(A, В, С)==А+ВС;

b) f{ А, В, С, D)AB+CD; ..-г) f(X, Y. Z)=XYZ+YZ;

д) f(A, В, С. D, E){A+C)D+ABCD.

о 1

в

Рис. у.1.1. Таблицы истинности и карты Карно для схемы полного вычитания.

лг -таблица нстииности; б -карта Карно для в; в -карта Карно для d.

У.1.2. Используя карты Карно, минимизируйте следующие функции:

а) n.X.Y, Z)=S(0, 1, 2.3.7. И. 15); б) /И. В, С) =2(3, 5. 6); в) X, У, Z)=S(4, 5, 8, 9, 10, 12, 13, 14);

г) /(Л, В, С, £))=зх(0, 4, 6, 7, 10, 12, 13. 14).

У. 1.3. Спроектируйте схему попарного умножения входных сигналов; А, В, С, D - входные сигналы; W, X, Y, Z - выходные сигналы.

У. 1.4. Таблица истинности и карты Карно для схемы полного вычитания приведены на рис. У. 1.1. Разработайте эту схему на вентилях НЕ-И.

У.1.5. а) Продолжите заполнение нижеследующей таблицы эквивалентности десятичных и двоичных целых чисел так, чтобы был охвачен диапазон десятичных чисел от О до 18.

б) Для десятичных чисел из диапазона 0-18 продолжите следующую таблицу значений двоично-десятичного кода:

в) На рис. У.1.2 приведена блок-схема преобразователя двоичных чисел в двоично-десятичное представление. Постройте логическую схему этого преобразователя на вентилях НЕ-И.

У. 1.6. На рис. У. 1.3 представлены технические характеристики 7-сегмент-ного дешифратора: положение каждого сегмента индикатора (с); колбина-

сигналы

-смналы

Рис. У.1.2. Преобразователь двоичных чисел в двоично-десятичное представление.

о 1 2

todupyeMbie значения

леремениой на Входе

jQ6ou4Hoe лредстаВ-ление де- сятичной лерембннои на Входе

Ряс. У.1.3. Данные для 7-сегментного индикатора.

й[ расположение сегментов индикатора; б - комбинации высвечиваемых сегментов; в блок-схема дешифратора; г - таблица соответствия входных и выходных сигналов.

ции высвечиваемых сегментов при индикации каждой цифры (б); блок-схема проектируемого дешифратора, преобразующего двоично-кодированные десятичные цифры в сигналы высвечивания сегментов индикатора (е); таблица соответствия высвечивания цифр комбинациям значений входных и выходных сигналов дешифратора (г). Разработайте схему дешифратора.

У.1.7. Используя карты Карно, минимизируйте следующие функции и разработайте схемы их реализации на вентилях НЕ-И: а) f(A, В, С)=Е(1, 4, 5, 6, 7); ( . Ь, с, d)=E(3, 4, 6, 7, 11, 12, 14, 15); X, У, Z)=E(1, 2, 4, 7); W. X, Y, Z)=E(0, 3, 4, 7, 8. И, 12. 15). У.1.8. Пусть на входы АВ и CD некоторой схемы поступают два 2-разрядных двоичных числа. Постройте эту схему на вентилях НЕ-И таким образом, чтобы она обнаруживала ситуации, когда АВ больше CD.

У.1.9. Спроектируйте на вентилях НЕ-И схему преобразования двоично-кодированных десятичных чисел в код Грея в соответствии с таблицей преобразования (табл. У.1.1).

Таблица У.1.1

Код Грея

двоично-кодированное десятичное число

Над Грея

ГЛАВА 2

МУЛЬТИПЛЕКСОРЫ

и ДЕМУЛЫИПЛЕКСОРЫ

В КОМБИНАЦИОННЫХ СХЕМАХ

Рассмотренные в гл. 1 методы удобны при проектировании логических схем с использованием вентилей НЕ-И или НЕ-ИЛИ в виде отдельных интегральных схем. При конструировании таких схем на пл1те требуется монтировать несколько интегральных схем. Между ними должны быть установлены связи в соответствии с соединительными линиями на логических схемах. В отдельных случаях число таких связей может быть значительным. При использовании печатных плат могут возникнуть значительные трудности при размещении соединительных проводников и минимизации их взаимного пересечения. Значительным может оказаться также объем пайки при монтаже.

Схемы со средним уровнем интеграции (СИС) значительно компактнее, чем стандартные интегральные схемы. При их использовании достигается экономия в количестве компонентов и межкомпонентных связей.

В этой главе рассматривается проектирование логических схем на основе СИС.

2.1. СТРУКТУРА МУЛЬТИПЛЕКСОРОВ

На рис. 2.1 изображена типовая (для среднего уровня интеграции) схема мультиплексора [9, 10, 29] с четырьмя входами, одним выходом (4X1) и двумя селекторными линиями. Селекторные линии обозначены X и У. С помощью подаваемых по ним сигналам осуществляется выбор одного из четырех входных вентилей подобно выбору отдельной клетки на карте Карно. В частности, при входных значениях XY=00 выбирается вентиль НЕ-И 201 (вход ао), при Л;У=01 - помеченный номером 202 вентиль НЕ-И (вход Ci). Аналогично при Л;У=10 происходит выбор вентиля 203 (вход Ог), а при Л;У=11-вентиля 204 (вход Пз).

Упрощенное символическое изображение мультиплексора, представленного на рис. 2.1, приведено на рис. 2.2. Для большей наглядности здесь сохранены буквенные обозначения шин входных и выходных переменных и селекторных сигналов. Ниже дополнительные обозначения не будут приводиться. Перечислим основные соглашения по изображению этих схем. Выход изобра-

жают только на длинной стороне прямоугольника. Всегда имеются два выхода, причем один из них соответствует инвертированному значению функции и изображается маленьким кружком со стрелкой.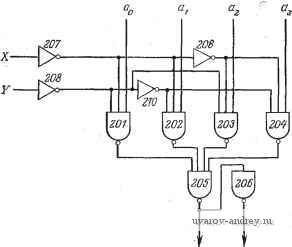

Селекторные линии

f f Выходы

Рис. 2.1. Типовая схема мультиплексора.

На короткой стороне прямоугольника при движении от выходных шин по часовой стрелке изображают шины селекторных сигналов. Линия младшего разряда селекторного кода располагается ближе всего к выходным сигналам. Входные шины изображают на другой длинной стороне прямоугольника. Она при-

Селек -

линии

Рис. 2.2. Символическое изображение мультиплексора.

Bccodbh

On а, ff.

f f.

мыкает к стороне селекторных шин и является следующей за ней при последовательном просмотре сторон прямоугольника по часовой стрелке. Линия самого младшего разряда ао располагается ближе всего к стороне селекторных шин прямоугольника.

Различают мультиплексоры типа 2x1 (одна селекторная шина), 4X1 (две селекторные шины), 8x1 (три селекторные шины), 16X1 (четыре селекторные шины) и т. д.

2.2. СИМВОЛИЧЕСКОЕ ОБОЗНАЧЕНИЕ ОПЕРАЦИЙ, ВЫПОЛНЯЕМЫХ МУЛЬТИПЛЕКСОРАМИ

В процессе проектирования операцию селектирования удобно представлять в следующем виде [11]:

[A][Z] = [/].

Входные данные записываются в виде матрицы [Л]. Например, [A] = [a(,ai] для мультиплексора 2x1, [Л] = [Qq йд] для мультиплексора 4x1,

и т. д., где ао, ai, ... - обозначения переменных на соответствующих входных линиях.

Матрица селектирования [Z] имеет вид

[Z] = [X] = [0 1] для мультиплексора 2x1,

для мультиплексора 4x1 и т. д.

Удобнее записывать комбинации двоичных значений на селекторных линиях десятичным числом. Поэтому для мультиплексора 4x1 пользуются также эквивалентной записью матрицы селектирования в виде

=[0 1 2 3].

Конечно, желательно, чтобы обозначения были как можно более компактными. Поэтому пользуются следующим простым обозначением матрицы селектирования:

При таком символическом обозначении придерживаются определенного порядка записи отдельных разрядов селекторной переменной. Старшие разряды записываются сверху, а младшие - снизу. Следует, однако, иметь в виду, что многие производители средств вычислительной техники придерживаются противопо-

ЛОЖНОГО порядка перечисления разрядов селекторной переменной.

Значения выходной переменной [/] могут быть получены применением операций логического умножения матрицы входных данных [А] на матрицу селектирования [Z].

Эти правила логического перемножения матриц распространяются также на более сложные случаи нескольких мультиплексоров и адресных линий микропроцессоров или мини-ЭВМ. При выполнении операции логического умножения значение выходной функции отождествляется с конкретной входной переменной (столбцом), выбираемой соответствующим значением l[Z]. Эта операция называется также адресацией.

Например, при [Z]=5 переменная [f] приравнивается входной переменной as, принадлежащей столбцу 5 матрицы [А] (номер крайнего слева столбца принимается за 0).

2.3. ПРИМЕНЕНИЯ МУЛЬТИПЛЕКСОРОВ В КОМБИНАЦИОННЫХ СХЕМАХ

Для иллюстрации использования мультиплексоров рассмотрим простой случай реализации логической функции ИСКЛЮЧАЮЩЕЕ ИЛИ на основе мультиплексора 4x1. Карта Карно для операции ИСКЛЮЧАЮЩЕЕ ИЛИ приведена на рис. 2.3. Вы-

Рис. 2.3. Карта Карно для операции ИСКЛЮЧАЮЩЕЕ ИЛИ.

ходная переменная, записанная в И-форме, имеет следующий вид:

/(Л,В) = 2(1,2).

Поскольку запись Z (1, 2) эквивалентна тому, что ai = a2=l, то

[ао ai 2 з! = [О 1 1 0].

Пользуясь операцией логического перемножения, это можно представить в следующем виде:

[0 110]

в

=[/].