жение отрицания функции f. В соответствии с этим имеем

J=XYZ

или, согласно правилам {и) и (к), 1.10. состояния БЕЗРАЗЛИЧИЯ

Во многих практических задачах существуют физические ограничения, приводящие к тому, что состояния, описываемые некоторыми клетками карты Карно, не могут порождаться схемой. Такие клетки рассматривают как клетки состояний безразличия. При минимизации представления функции эти клетки можно

00 01 11 10

00 01 П 10

Рис. 1.32. Карта l=XZ с состояниями безразличия.

подключать к любой группе. Состояние безразличия можно отображать в соответствующей клетке знаком ф и считать его либо 1, либо О по желанию конструктора. Карта с состояниями безразличия изображена на рис. 1.32. Включив одну из таких клеток в группу, определяющую функцию, получаем минимизированное представление f=XY на основе четырех клеток карты.

1.11. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Практическая реализация логических функций предполагает составление логических схем (рис. 1.33). Рассмотрим функцию 5Р-типа

f = WX-\-YZ.

Начиная анализ с левой части рис. 1.33, отметим, что инвертор (НЕ) использован для изменения знака переменной W на обратный. Далее реализуется выражение WX с помощью венти-

т

О

т

Рис. 1.33. Логическая схема для функции f=WX+YZ.

ЛЯ И. Аналогичным образом реализуется выражение YZ. Выходы обоих вентилей И соединены со входами вентиля ИЛИ. Выходной сигнал вентиля ИЛИ и есть значение функции f.

1.12. РЕАЛИЗАЦИЯ ФУНКЦИИ НА ВЕНТИЛЯХ НЕ-И

С распространением интегральных схем большое значение приобретает использование вентилей типа НЕ-И. Чтобы показать, как реализуется функция на этих вентилях, введем на рис. 1.33 указатели инвертирования на выходе вентилей И и входах вентиля ИЛИ. Согласно правилу {и), двукратное инвертирование не приводит к изменению сигнала. Как показано на рис. 1.17,

~tw\-

X-Y-

У

(ЗкВивалент

ту--/

Рис. 1.34. Реализация функции f=wX+YZ на интегральных схемах типа НЕ-И.

вентиль И с инвертированным выходом является вентилем НЕ-И. Из рис. 1.19 следует, что вентиль ИЛИ с инвертированными входами также представляет собой вентиль НЕ-И. На рис. 1.34 показана простая схема реализации функции fWX+YZ на интегральных схемах типа НЕ-И. Пользуясь правилом (ы), можно показать, что WX=W+X и YZ=Y+Z.

1.13. РЕАЛИЗАЦИЯ ФУНКЦИИ НА ВЕНТИЛЯХ НЕ-ИЛИ

Построение схем на вентилях НЕ-ИЛИ включено в данный материал в целях полноты, хотя и не рассматривается в этой книге как базовый элемент конструирования. Функция SP-типа

f = WX + YZ,

может быть записана в PS-форме как

f = {W+Y) (W+Z) (X-j-Z).

Она может быть реализована на И- и ИЛИ-вентилях, как показано на рис-. 1.35. Введение указателей инвертирования на обоих

у

Ш

E>-iL

Ч1>С

1/2:

Рис.. 1.35. Логическая схема для функции f=(W+Y){W+Z){X+Z){X+Y). а-с вентилями И и ИЛИ; 6 -с вбитилями НЕ-ИЛИ.

концах каждой из линий - входов сумматора (т. е. на выходе вентиля ИЛИ и входе вентиля И), согласно правилу (ы), не нарушает функционирование схемы. При этом схему оказывается возможным легко построить на однотипных вентилях. На рис. 1.35,6 показана реализация той же функции на вентилях НЕ-ИЛИ.

Обычно реализация функции на вентилях НЕ-ИЛИ проще при использовании J в SP-форме с последующим инвертированием результата. Иногда подобное решение оказывается проще при использовании вентилей НЕ-И.

1.14. ПРИМЕРЫ РЕАЛИЗАЦИИ Карте на рис. 1.28 соответствует функция

f = WY-\-YZ-\-WX. Реализация этой функции на вентилях НЕ-И показана на

рис. 1.36, а. Вентили НЕ-И выпускаются с двумя, тремя, четырьмя и восемью входами. Имеются интегральные схемы, содержащие четыре двухвходовых, три трехвходовых, два четырех-входовых и один восьмивходовый вентили. На рис. 1.36,6 дан пример реализации функции f=WXY+WXZ с использованием трехвходовых элементов.

i Z

У

>

т

У

т

У

~1з$у-

Рис. 1.36. Логические схемы на вентилях НЕ-И.

о-для функции f=WY+YZ+WX; б - для функции f=WXY+WXZ.

1.15. ИСКЛЮЧАЮЩЕЕ ИЛИ

Наряду с операциями И и ИЛИ, практически реализуемыми в виде вентилей НЕ-И и НЕ-ИЛИ, используются некоторые другие функции, например такие, как ИСКЛЮЧАЮЩЕЕ ИЛИ. Операции, выполняемые этой функцией над переменными, полностью подобны употреблению союза или в обычной разговорной речи. Эта функция в SP-форме имеет вид

f = AB+AB.

О 1

т

т

>

Рис. 1.37. Функция ИСКЛЮЧАЮЩЕЕ ИЛИ.

а - карта Карно ИСКЛЮЧАЮЩЕЕ ИЛИ; б - реализация минимизированного представления функции F=AB+AB=AQB.

Карта Карно для нее показана на рис. 1.37, а. Схема реализации минимизированного представления этой функции, приведенная на рис. 1.37,6, получена методом минимизации схем с использованием их карт Карно. Схемное решение может быть также упрощено объединением отрицательных переменных в произведение следующим образом:

/= (Л-f 5) {А + Б) = {ЛВ) (Л + В). Соответствующая логическая схема показана на рис. 1.38. Полу-

т

У

т

А + В

А ®в

Рис. 1.38. Упрощенная логическая схема для f-=A@B.

чена экономия в один вентиль. Эта схема настолько важна, что для нее вводят знак операции ® и специальный графический символ, изображенный на рис. 1.39, а. В данной книге будет использоваться упрощенный графический символ (рис. 1.39,6).

А№В

А

В

А® в

152 В

Рис. 1.39. Графическое обозначение операции ИСКЛЮЧАЮЩЕЕ ИЛИ.

а - стандартное обозначение; б - упрощенное обозначение.

1.16. СИММЕТРИЧНЫЕ ФОРМЫ

На рис. 1.40 изображена карта Карно для часто используемой при проектировании логических схем функции, симметричной относительно входных переменных W, X, Y м Z. На рис. 1.41, с

показана реализация этой функции в виде древовидной схемы, а на рис. 1.41,6 - в виде несбалансированной схемы. Можно отметить, что для первого варианта реализации между любым входом и выходом имеются два вентиля ©, тогда как во втором варианте число вентилей между отдельными входами и выходом равно трем.

Рис. 1.40. Карта Карно для функции f{W, X, Y, Z), симметричной относительно входных переменных.

00 01 11 10

Положение отдельных звеньев логической схемы относительно выхода принято характеризовать величиной так называемого уровня. При определенном значении уровня для выхода вентиля НЕ-И считается, что его входы расположены на следующем более высоком уровне. Если приписать выходу уровень О, то входы выходного вентиля следует считать принадлежащими уровню 1. Аналогично и для последующих вентилей переход от вы-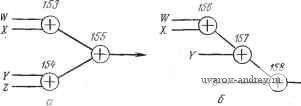

Рис. 1.41. Логические схемы для симметричной функции, о - древовидная схема; б - несбалаисированная схема.

.Хода к входу увеличивает уровень на 1, так что на рис. 1.38 может быть выделено три уровня удаленности входов вентилей от окончательного выхода. Каждому такому уровню, характеризующему прохождение сигнала через вентиль реальной электрической схемы, соответствует определенная величина задержки. Учет временных задержек оказывается важным при анализе

функционирования некоторых специальных логических схем (см. гл. 5), а понятие уровня может успешно применяться и при конструировании комбинационных схем специального назначения.

I.I7. РЕДУКЦИЯ

В разд. 1.15 приведены примеры реализации функции ИСКЛЮЧАЮЩЕЕ ИЛИ {§=АВ+АВ) как на основе минимизированного представления на пяти вентилях (рис. 1.37), так и в более упрощенном виде на четырех вентилях (рис. 1.38). Систематизированная процедура упрощения называется редукцией, поскольку в ряде случаев она приводит к уменьшению числа используемых вентилей. В этом разделе методика редукции рассматривается детальнее.

Рис. 1.42 представляет собой повторение рис. 1.38 с дополнительным изображением уровней соединительных цепей. Для

Уродень 3

Уровень 2

Уровень 1 Уровень

т

Рис. 1.42. Логическая схема для /=ЛФВ с изображением уровней соединительных цепей.

SP-формы функций четные уровни соответствуют минимальным, а нечетные - максимальным комбинациям переменных. В частности, нулевой уровень соответствует функции на выходе.

Каждый вход на уровне 1 обычно должен представлять максимальный терм, подлежащий операции И при получении инвертированного значения требуемой функции. Уровень 3 представляет максимальный терм, подлежащий изъятию из уровня 2. Для уменьшения числа вентилей все входные сигналы должны быть положительными. Поэтому при использовании функции АВ

00 01 11 10

А-В

В-С

А С-

Рис. 1.43. Выполнение процедуры редукции.

Рис. 1.44. Логическая схема функции /=ЛВ-1-ВС-1-ЛС.

на входе уровня 3 (рис. 1.42) удаляется клетка 3 из функции уровня 2.

В качестве еще одного примера рассмотрим процедуру редукции функции, представленной картой на рис. 1.43. Если игнорировать значение функции в клетке 7, то эта функция может быть реализована посредством трех переменных на уровне 2, как показано на рис. 1.44. Для правильной реализации требуемой функции из полученного решения должна быть удалена клетка ABC. Это достигается размещением входных переменных для клетки ЛВС на уровне 3 (рис. 1.45).

ledy-

f=/IBC+m+ABD

Рис. 1.45. Реализация функции f=ABC+ABC+ABC при выполнении редукции.

1.18. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ РЕШЕНИЯ

Имеется множество примеров практического использования вентилей НЕ-И при проектировании логических схем. В общем случае такие схемы можно классифицировать либо как генераторы функций, либо как дешифраторы. Примером генератора функции служит сумматор двоичных чисел с формированием сигнала переноса (рис. 1.46). Входными сигналами блоков О, 1, 2 и 3 являются

Л = аЗ а2 а\ сО и В = Ь2, Ь2 Ы ЬО,

Ьг aZ

с2 s2

с1 si

bO аОкО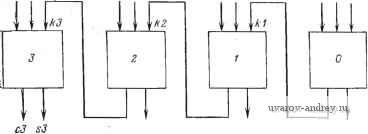

сО sO

Рис. 1.46. Блок-схема сумматора двоичных чисел,

определяющие значения двоичных разрядов двух суммируемых чисел. Поступающий на те же блоки входной сигнал

K=kZlk2 k\ kO

образован битами переноса, порожденными предыдущим двоичным сложением. Самыми старшими значащими битами (СЗБ) входных сигналов являются аЗ, ЬЗ и кЗ, а самыми младшими значащими битами (МВБ) - аО, ЬО и kO. Выходными сигналами являются

С=сЗ с2 с1 сО и S = s3 s2 si sO,

где С и S - двоичные числа, обозначающие перенос и сумму соответственно.

Для простоты дальнейшего изложения выполняемые каждым отдельным блоком преобразования показаны в табл. 1.6, где abk=an Ьп kn и cs = cn sn при п=0, 1, 2, 3. Процесс проектирова-Таблица 1.6 ия сумматора сводится к следующим шагам:

1) определению входных и выходных сигналов;

2) построению карт Карно для выходных величин, при этом значения входных величин должны определять соответствующие строки и столбцы этой картины;

3) записи логических выражений для каждой выходной переменной как функции входных переменных;

4) изображению схемы как минимизированной комбинации вентилей НЕ-И.

Соответствие входных и выходных переменных для сумматора

Входы

Рис. 1.47. Карты Карно для сумматора.

о - для переменной с; б - для переменной s.

а

>

>

ie8y>-

- с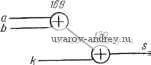

Рис. 1.48. Логические схемы для сумматора.

Таблица 1.7

Соответствие входных и выходных переменных для 4-разрядного генератора функции ysinx

Васды