Задумывались ли вы, почему современные методы проектирования называют логическими ? Анализ наиболее интересных разработок в области конструирования ЭВМ показывает, что в этих технических решениях содержатся и элементы, произвольно выбираемые конструкторами. Не существует также логически-однозначных методов оптимизации функционирования мини-ЭВМ и микропроцессоров. Почему же говорят о логических методах проектирования? Законы логического мышления систематически исследовались английским математиком Дж. Булем [1]. Он разработал метод проверки истинности определенных высказываний. В рамках этого подхода различные возможности фиксируются в виде предложений, и к этим высказываниям применяются специальные операции объединения и вывода логических следствий. Таким образом, понятия истинности и ложности берут свое начало в исчислении высказываний, приводящем к современным методам проектирования с использованием таблиц истинности. Структура современных таблиц истинности отличается от первоначальной, но термин логическое применительно к конструированию продолжает использоваться.

В булевой алгебре определяется ряд операций, достаточно удобных для использования при логическом конструировании. Можно заметить, однако, что в булеву алгебру входит операция, без которой при этом можно обойтись, и в то же время в ней отсутствуют некоторые весьма удобные операции. В соответствии с этим логику проектирования удобнее представлять математическим аппаратом алгебры переключательных схем, получившей развитие в работе Шеннона, Венна и Карно [2] и обсуждаемой в данной главе. В частности, здесь рассмотрены методы описания и проектирования переключательных схем посредством карт, дающих графическое представление используемых операций. Они используются во всех последующих главах.

1.1. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

В алгебре переключательных схем имеются по существу всего три основные операции. Другие операции могут быть построены как их комбинации. Чтобы проиллюстрировать смысл этих ос-

новных операций, рассмотрим прямоугольник, представляющий множество всех элементов, к которым эти операции применимы. Подмножество точек прямоугольника может быть изображено кругом внутри него. Два подмножества У и Z представляются в виде двух кругов внутри одного и того же прямоугольника

Рис. 1.1. Множества и подмножества.

Рис. 1.2. Определение операции И, YZ.

(рис. 1.1). Исходя из такого изображения, называемого диаграммой Венна, может быть определена операция И, обозначаемая также символом . Заштрихованная область на рис. 1.2 представляет объединение подмножеств, описываемое выражением Y-Z, и является графической иллюстрацией определения операции И.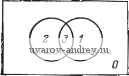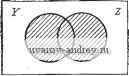

Рис. 1.3. Нумерация областей на диаграмме Венна.

Рис. 1.4. Определение операции ИЛИ,

y+z.

Операция И относится к основным операциям алгебры, поскольку обеспечивает выбор определенной минимальной области'). Четыре такие минимальные области изображены на рис. 1.3. Абсолютная минимальная область в рассматриваемом прямоугольнике является пустым множеством, но это не представляющий особого интереса вырожденный случай. Операция И используется по существу для определения одного из основных подмножеств точек.

1 Под минимальной областью здесь понимается множество точек е определенным сочетанием состояний принадлежности этих точек множествам Y и Z и их дополнениям У и Z. Минимальные области являются графическими аналогами используемого далее в разд. 1.4 понятия минитерма. - Ярмж. перев.

:: Заштрихованная область на рис. 1.4 представляет действие операции ИЛИ, которая обозначается символом +. Не следует удивляться использованию знака +. На любой пишущей машинке, как и в любом типографском наборе литер, имеется достаточное количество знаков для выражения основных операций. Использование знака + для обозначения тех или иных операций является результатом договоренности.

Рис. 1.5. Изображение области У.

Операция ИЛИ применяется для выделения максимальной области внутри прямоугольника, если исключается предельный случай охвата всей площади. Выделение максимальной области и определяет пользу и назначение этой операции.

Операции и + ограничены в своих возможностях выделять подмножества. В связи с этим вводится также основная операция НЕ (рис. 1.5). Действие операции НЕ на подмножество У представлено на этом рисунке заштрихованной областью. Операция НЕ обозначается символом ~. Заштрихованная область на рис. 1.5 обозначается как У и читается не У . Эта операция позволяет распространить действие операций И и ИЛИ на другие подмножества. :

1.2. ТАБЛИЦЫ ИСТИННОСТИ

Вместо диаграмм Венна производители интегральных схем для вычислительной техники обычно пользуются таблицами истинности. Использование этих таблиц основано на несколько иных

Таблица 1.1

Таблица истинности для операции И

Таблица 1.2

Таблица истинности для операции ИЛИ

Таблица 1.3

Цифровое обозначение областей для операции YZ

соглашениях и обозначениях. Однако таблицы истинности могут быть однозначно сопоставлены приводившимся выше диаграммам. Если принадлежность произвольной точки прямоугольника множеству Y (или Z) считать истиной (с обозначением Т или 1), а противоположный случай - ложью (jF или 0), то таблица истинности для операции И может быть изображена в виде табл. 1.1. Таблица истинности для операции ИЛИ приведена в табл. 1.2, Заметим, что в этих таблицах представлены четыре различные комбинации случаев принадлежности (или непринадлежности) точки множествам У и Z. Каждая из комбинаций отвечает определенной помеченной цифрой области из изображенных на рис. 1.3. Комбинации для операции YZ и соответствующие им цифровые обозначения областей показаны в табл. 1.3.

1.3. ИЗОБРАЖЕНИЕ ПРЕОБРАЗОВАНИЙ ВХОДНЫХ ВЕЛИЧИН В ВЫХОДНЫЕ КАРТАМИ КАРНО

Несмотря на то что диаграммы Венна удобны при первоначальном обучении, а таблицы истинности используются для описания функционирования интегральных схем, ни один из этих способов изображения нельзя признать плодотворным при освоении современных методов логического конструирования. Удобнее оказывается использовать так называемые карты Карно [2-8].

Рис. 1.6. преобразование диаграммы Венна в карту Карно.

с - шаг I; б - шаг 2; е - шаг 3.

На рис. 1.6 показано преобразование диаграммы Венна в карту Карно. Видно, что последняя имеет более простой вид. Такое же преобразование в карты Карно может быть выполнено и для таблиц истинности (рис. 1.7). Использование карт Карно обеспечивает более компактное и наглядное изложение материала. При этом выполняемые операции принято описывать в дру-

гих терминах. Множества или переменные К и Z называют

о f

Рис. 1.7. Таблицы истинности в форме карт Карно.

а - операция И; б - операция ИЛИ-

входными величинами (входными переменными). Логическая операция определяет значение выходной величины (функции). На карте Карно входные величины обозначены сверху и слева. Карта состоит из нескольких клеток. Указание конкретных клеток в карте определяет ту или иную логическую операцию. Поскольку рассматривать приходится все клетки, о такой структуре и говорят как о карте.

1.4. МИНИМАЛЬНЫЕ ФОРМЫ

Клетки карты Карно нумеруются так, чтобы та или иная комбинация входных переменных была определена однозначно. Так, на карте, изображенной на рис. 1.8, клетка О соответствует значениям входных переменных У и Z, клетка 1 - значениям У и Z, клетка 2 - значениям У и Z, а клетка 3 - значениям У и Z. В клетках карты можно указать значения логической функ-

Рис. 1.8. Нумерация клеток карты Карно.

ции и для соответствующих комбинаций значений входных переменных, заданных непосредственно или в инвертированном виде. Функция, определяемая всеми возможными значениями входных переменных, может рассматриваться как разложение по мини-термам [2]).

Минитермом (элементарной конъюнктивной формой) принято называть конъюнкцию из нескольких двоичных переменных, в которой каждая переменная присутствует либо непосредственно, либо в виде отрицания.- Прим. перев.

Удобной формой записи значений функции И является S(3). Этой записи соответствует клетка 3, т. е. входные переменные со значениями У и Z. Следовательно, функция f{Y, Z) имеет вид

f{Y,Z)=Y.Z={3).

Так определяется операция И. Аналогично

/(F.Z) = E(0) = F.Z, f(Y,Z)-E(l)=Y.Z, f{Y,Z)=-L{2)==Y.Z.

Удобно обозначение f{Y, Z) сократить до f, а У-Z - до YZ. Такие сокращенные обозначения широко используются в этой книге.

1.5, МАКСИМАЛЬНЫЕ ФОРМЫ

На рис. 1.9 даны цифровые обозначения клето^ для операции ИЛИ. На рис. 1.9, а представлена функция Y+Z. Пусть в соответствии с принятыми выше обозначениями для операции ИЛИ

Рис. 1.9. Карты Карно для функций я(0), я(1), я(2) и я(3).

а - функция y+Z; б - функция Y+Z; в - функция y+Z; г - функция Г+Z.

в данном случае цифрой О помечаются те клетки карты Карно, в которых функция У-f Z имеет единичное значение. Для функций y+Z (рис. 1.9,6), y+Z~(pHc. 1.9, в) и y-fZ (рис. 1.9, г) подобные клетки карт Карно обозначены цифрами 1, 2 и 3 соответственно. Эти функции составляют полный набор максимальных

невырожденных функций; буква п. Так,

для их обозначения используется

n{0)=Y+Z. я(1)=К+2,

n(2) = F-fZ. 3X(3) = F+Z.

Если f{Y, Z)=n(0) hT{Y, Z)=jt(6)), TO рис. 1.10 дает компактное представление я-карт для функции YZ.

Рис. 1.10. Компактное представление я-карт.

Представление функции в такой форме называется представлением посредством макситермов.

Рассмотрим функцию, заданную картой на рис. 1.11, а. Эта функция может быть сформирована одним из двух методов:

1) построением максимальной комбинации минимальных форм;

О 1

у

а и о

Рис. 1.11. пример построения функции в виде комбинаций минимальных или максимальных форм.

с -карта функции \(y, z): б - минимальные формы; в - максимальные формы.

2) построением минимальной комбинации максимальных форм.

Минимальная форма показана на рис. 1.11,6. Верхняя левая клетка S(0) представляет YZ, а нижняя правая клетка S(3) соответствует YZ. Взяв максимальную комбинацию этих двух кле-

Краткую формулировку автора следует понимать следующим образом: если ввести специальное обозначение i (i=0, 1, 23) и для n{i)==f{X, Z) считать n(i)=f{X, Z) (т. е. по существу я(1)я{0), то в виде рис. 1.10 можно компактно изобразить множество всех невырожденных максимальных функций. - Лриж; перев.

ТОК, получим результирующую функцию /:

f.= YZ-\-YZ.

Любая функция, имеющая подобный общий вид, называется суммой произведений (SP). Таким образом обозначается максимальная комбинация минимальных форм. Функция / может быть также записана в форме

/=2(0), 2(3), или /=2(0,3).

На рис. 1.11, в изображены максимальные формы. Группа клеток зт(2) в правом верхнем углу представляет Y+Z, а груп-

б

О

00 01 11 10

Рис. 1.12. Построение карты для трех переменных.

о - шаг 1; 6 - шаг 2; в - шаг 3.

па я(1) в левом нижнем У-i-Z. Их минимальная комбинация определяет выходную функцию / в виде

/=(F--Z).(F+Z).

Функция такого вида называется произведением сумм (PS) и выражает минимальную комбинацию максимальных форм. Рассматриваемая функция может быть записана в виде

/=я(1), я(2), или /=л(1,2).

В этой книге в основном используется представление функций в виде разложения по минитермам (SP-форма).

1.6. РАЗЛОЖЕНИЯ ПО МИНИТЕРМАМ

На рис. 1.12 для переменных Л, Б и С показано, как легко распространяется этот метод представления на случай трех переменных. На рис. 1.12, а изображены области, обозначающие каждую из переменных. На рис. 1.12,6 представлена стандартная форма карты, а входные переменные указаны вдоль ее сто-

Рис. 1.13. S-нумерация клеток карты.

целесообразно по ряду причин. Одна из них связана с особенностями производства интегральных схем. Эти схемы должны выполняться, так, чтобы сигнал на выходе изменял свою полярность. В терминах переключательных схем это эквивалентно операции отрицания (НЕ) над выходным сигналом. Поэтому наряду с основными логическими операциями И и ИЛИ целесообразно рассматривать тесно связанные с ними логические операции отрицания значения на выходе. На рис. 1.15 изображены /С-карты для операций И и ИЛИ и символы для их графического изображения. На рис. 1.16 показано стандартное обозначение для логической операции НЕ. Маленький кружок на схемах применяется для обозначения инверсии. Цифры (101, 102 и 103) помещены в графические символы вентильных схем в

Таблица 1.4 рон. На рис. 1.12, в сверху и слева от Минитермы в случае клеток карты изображены возможные

трех переменных значения трех переменных так же,

как это принято в таблицах истинности. Для удобства минитермы для случая трех переменных ABC представлены в табл. 1.4.

На рис. 1.13 показана 2-нумера-ция клеток карты. Аналогично могут быть составлены карты Карно для четырех и большего числа переменных. На рис. 1.14, а показано соответствие клеток карты Карно отдельным переменным, а йа рис. 1.14,6 представлена 2-нумерация клеток карты, соответствующая нумерации минитермбв.

Далее в книге карты Карно будут называться /С-картами или просто картами.

1.7. ГРАФИЧЕСКИЕ ОБОЗНАЧЕНИЯ

Работу различных схем удобно описывать диаграммами. Для этой цели применяются специальные символы, обозначающие как основные, так и производные логические операции. Использование специальных обозначений для производных операций

Рис. 1.14. Карта Карно для четырех переменных.

о - соответствие клеток карты отдельным переменным; б - Z-нумерация клеток.

Рис. 1.15. Символы операций И и ИЛИ.

а - операция И; б - операция ИЛИ.

Г

>

g>

Рис. 1.16. Символ операции НЕ.

Рис. 1.17. Символы операций НЕ-И и НЕ-ИЛИ.

а - операция НЕ-И; б - операция НЕ-ИЛИ.

, б