Действующие значения токов вентилей

/, = /д

-=57,8 А.

Действующее значение тока вентильной обмотки трансформа-

-jlsz - 3 -si -sz is3 -SI -sz lisJ <J-si

Pnc. 2.95. Диаграммы напряжений и токов в схеме на рис. 2.94.

Задача 2.51, Для схемы выпрямителя, показанной на рис, 2.9G, определить среднее значение выпрямленного напряжения и состав гармоник выпрямленного напряжения, если дано, что про-всапмость непрерывная.

Рещение. Два последовательно сое,щшенных трехфазных моста разделяются на четыре отдельные коммутационные группы. Ко.ммутацпя каждой группы ие зависит от остальных трех. Поэтому среднее значение выпрямленного напряжения равно сумме средних значений выпрямленных напряжений двух мостов, т. е.

t/dio=2-2,34f;..

Суммировать можно и мгновенные значения. Так как выходные напряжения двух шестипульсных мостов смещены по фазе на 30°, то представленная на рис. 2.96 схемг будет двенадцатипульсной, следовательно, выпрямленное напряжение будет содержать следующие гармоники:

п=ср= 12, 24, 36...

Задача 2.52. Определить среднее значение выпрямленного напряжения для выпрямителя со схемой соединений, показанной на рис. 2.97, при условии, что проводимость вентилей непрерывная. Трансформатор и диоды идеальные.

Решение. Схема соединений может быть разложена иа , две независимые коммутационные группы, диоды каждой групггы НО-коммутируют между собой неза- ц-висимо от диодов другой группы. ~uj

в группе / тот диод проводит I ток, анод которого имеет наи- ° большее положительное напряже- p c. 2.96. Схема выпрямителя ние. Поскольку одно из снимет- к задаче 2.51.

ричных фазных напряжений всегда больше нуля, диоды Да, Дь и Дс никогда не проводят ток.

В группе тот диод проводит ток, катод которого имеет наибольшее отрицательное напряжение. По причинам, указанным выше, диоды Да, Де н Д/ никогда не проводят ток.

Вследствие этого схема соединений становится простой схемой выпрямителя ЗФ2Н6П, в которой

Udio 2V2~Us~ sLn ~=2.34Us.

2.4. ЗАДАЧИ ПО ПРЕОБРАЗОВАТЕЛЬНЫМ ТРАНСФОРМАТОРАМ

Задача 2.53. Идеальный выпрямитель со схемой соединений 1Ф1Н1П, работающий на активную нагрузку, присоединен к сети через однофазный трансформатор с идеальной магнитной системой (рнс. 2.98). Поток рассеяния трансформатора пренебрежимо мал. Построить кривые токов в обмотках трансформатора и найти .средние и действующие значения токов при условии, что активное сопротивление цепи сетевой обмотки, отнесенное к вентильной обмотке, равно Rp, а активное сопротивление цепи вентильной обмотки вместе с нагрузкой равно Rs-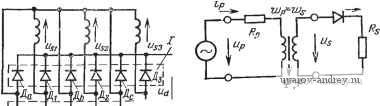

Рис. 2.98. Схема однофазного однонаправленного одноимпульсного выпрямителя к задаче 2.53.

Рис. 2.97. Схема выпрямителя к задаче 2.52.

Решение. По условию поток рассеяния трансформатора равен нулю, поэтому тра.нсформатор может быть заменен реактивным сопротивлением, через которое протекает ток намагничивания / (рис. 2.99). Благодаря наличию диода ток вентильной обмотки и, как показано на рис. 2.100,а, является пульсирующим током одного знака. Он может быть разложен на постоянную составляющую /.

и переменную составляющую i (p c. 2.100,6, е). Предположим в первом приближении, что токи в двух других ветвях эквивалент-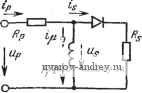

Рис. 2.99. Эквивалентная схема к задаче 2.53.

Р.чс. 2.100. Диаграммы токов на стороне вентильной обмотки трансформатора (к задаче 2.53).

ср

Zx зх

ait

ной схемы будут иметь ту же самую форму, т. е. i

t = / -1- t

h = fpcp + ipa-

Поскольку ip = i + js, TO для составляющих токов будут справедливы следующие уравнения:

Предполагая, что сердечник трансформатора имеет неограниченно большую магнитную проницаемость и может иметь неограниченно большую магнитную индукцию (рис. 2.101), получаем ц, = = 0, а токи сетевой и вентильной обмоток равными:

ip = h fpcp - fscp> ipz = sz.

Однако такой идеальный трансформатор очень сильно отличается от любого реального трансформатора. Это видно из рассмотрения уравнений напряжений

Uj,=lpRp-\-Us.

Напряжение Us возникает при изменении во времени потоко-сцепления обмотки:

с№ dt

Ток сетевой обмотки содержит постоянную составляющую. Б цепи ет источника постоянного напряжения, поэтому постоянная составляющая тока может быть скомпенсирована только за счет постоянной составляющей индуцированного напряжения dW/dt. Из этого следует, что уравнения напряжений можно разделить на

в

Рис. 2.101. Характеристика намагничивания идеального не-иасыщающегося стального сердечника трансформатора (к задаче 2.53).

Рис. 2.102. Характеристика намагничивания идеального насыщающегося стального сердечника трансформатора (к задаче 2.53).

уравнения для постоянных и переменных составляющих:

где Fl обозначает ту часть потокосцепления обмотки трансформатора, которая изменяется линейно во времени (т. е. индуцирует постоянное напряжение), а обозначает ту часть потокосцепления, которая .вызывает появление переменного напряжения. Так как первая составляющая потокосцепления изменяется с постоянной скоростью, то

.-rf<-=-/pcp?P = const.

В действительности сердечник трансформатора имеет ограниченную насыщением стали магнитную индукцию. Пользуясь идеальной кривой намагничивания с учетом насыщения (рис. 2.102), которая ближе соответствует действительной кривой намагничивания, нетрудно видеть, что описанная выше работа трансформатора с нагрузкой, состоящей из однонаправленного выпрямителя, невозможна. Насыщение сердечника не позволяет потокосцеплению выходить за пределы или -Fs. Следовательно, при насыщении трансформатора должно выполнятьсяследующее условие:

/р cpRp-0.

Поскольку по условию задачи сопротивлением Rp нельзя пренебречь, то только Ip CP может быть paBiHo нулю, т. е. через сетевую обмотку трансформатора будет протекать только переменный ток. Таким образом, уравнения для токов при насыщении трансформатора примут вид:

Отсюда видно, что апериодическая составляющая тока намагничивания трансформатора с насыщающимся сердечником и нагрузкой, состоящей из однонаправленного вьшрямителя, будет равна среднему значению тока вьшрямителя, т. е. .появится МДС, приводящая к одностороннему намагничива>н1ию сердечника трансформатора. На рис. 2.103 показаны кривые, характеризующие процесс намагничивания. Сначала тока насыщения нет, среднее значение потокосцепления уменьшается линейно, и ip=is, aJjc=0, при этом положительные и отрицательные производные потокосцепления не равны, поскольку положительные напряжения Us отличаются от отрицательных на падение напряжения ipRp.

Когда яотокосцепление достигнет значения - Ws, дальнейшее его изменение прекратится, т. е. dW/dtO и, следовательно, Us-0, ток сетевой .обмотки - будет ограничиваться только активным со- противлением Rp. Имен-

- но эти отрицательные

Р Г\ Г\ импульсы тока иамагии-

(ut чивают трансформатор. Форма кривой и действующее значение тока сетевой обмотки отличаются от формы кривой и wt действующего значения гока вентильной обмот-ки. Вычислим угол О, в течение которого сердечник трансформатора на-vy ходится в насыщенном

N I состоянии, н дополняющий его до 2.rt угол %.

Рис. 2.103. Диаграммы работы однофазного трансформатора с идеальным насыщающимся сердечником, работающего в однонаправленной однопульсной схеме (к ехип задаче 2.53).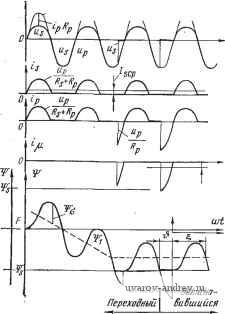

в установившемся режиме изменение магнитного потока за период равно нулю:

и, следовательно, равен нулю интеграл напряжения на вентильной обмотке:

Usd-z= К2 Up j sintoxtT: + j ГУ sin owfw = 0. После интегрироваш1я н преобразований получаем:

Ss - Rp

Rs - Rp

Среднее значение тока намагничивания равно:

1 С YYu У2и„

- \ Psincotrfx- Р(-1+cos), ,.

j R 27l/?p

V2 [/

K2- t/p

- П y? +

Теперь из

/.чгл-

Р- SI Л^ + /?р

получаем, что 7 = -/ср. т- е. /рср=0.

Далее найдем действующее значение тока ip. Имеем:

Интегрируя, получаем:

; + ! 1} ] (2- + sin cos

4 V s + Rp У 4к

Для малых углов 6 =isin6. По определению 2к- = в. Подстав ляя sln = -siiift и преобразуя, получаем:

р- 2{Rs + Rpr

Г 2m%{RsRp)

Поскольку sin

V2 U

2(Rs + Rp) шосле некоторых преобразований найдем:

Видно, что действующее значение тока сетевой обмотки в результате одностороннего намагаичивания увеличивается. Например, если Rs=50Rp, то /p= 3/s. Ситуация в реальном трансформаторе лучше, так как в нем магнитный поток продолжает изменяться

1р

с

Ч>1-

Рис. 2.104. Однофазный выпрямительный броневой трансформатор (к задаче 2.54).

;Рис. 2.105. Диаграммы работы выпрямителя на рис. 2.104.

и лл изгибом петли гистерезиса. Это означает, что к трансформатору продолжает прикладываться напряжение и тем самым ограничивается рост намагничивания.

Вследствие одностороннего намагничивания трансформатора схема 1Ф1Н1П применяется только в слаботочной технике.

Задача 2.54. Определить ток сетевой и вентильной обмоток и мощность трансформатора (отдельно для броневого и стержневого), питающего вьшрямитель со схемой соединений 1Ф1Н2П Нагрузка на выпрямитель состоит из резистора с сопротивлением Rd и реактора с индуктивностью Ld- В броневом трансформаторе сетевая и вентильные обмоткн расположены на одном и том же стержне магнитопровода (рис. 2.104). Кривая тока вентильных обмоток имеет форму прямоугольного импульса (рис. 2.105,6, в). Ре-

зультирующая МДС в среднем стержне будет: т. е.

is,) +

Поскольку ток is2- 1 переменный, условие /р ср=0 удовлетворяется только для случая, когда fo=0 (см. задачу 2.53). Соответственно кривая тока 1р имеет форм.у, как показано на рис. 2.105,г..

Расчетная мощность трансформатора определяется следующие образом:

Isi-Is2 - yY

Ip=ld-

Ss = Us,U + Us,h,=V2 Upla;

Sp = UpIp-

1 r. r. ®S 1 +K2

S= - (.Ss + Sp)=UpIa-2-

Поскольку

и

то находим:

S = 7t

r, P

UiIi=Pi,

в стержневом трансформаторе обмотки располагаются на двух отдельных стержнях магнитопровода (рис. 2.106). Кривые токо . вентильной обмотки (рис. 2.107,6, в) такие же, как и в случае а .. Для того чтобы найти ток сетевой обмотки, запишем выражения; для МДС в стержнях (МДС в ярмах можно пренебречь):

f01 = - ip ~2~ + Рог

Р 2

issWs;

Эта система уравнений решается следующим образом:

Fn = W.-n- = W:

Построив на основе этого уравнения зависимость тока сетевой юбмотки от времени (рис. 2.107,г), можно получить также МДС одностороннего намагничивания путем последовательных вычислений МДС в стержнях магнитопровода от одного полупериода к другому.

Wp/Z

Рис. 2.106. Однофазный выпрямительный стержневой трансформатор (к задаче 2.54).

. Рис. 2-107. Характеристика диаграммы работы вьшрямителя на рис. 2.106.

Расчетная мощность трансформатора вычисляется следующим образом:

Isi - Isz - 2

I = Id

Us,=Us.=

Up Ws 2 w7

pi - 4p2 - 2

S.= 2Us,Isi=y2

Upld,

Sp = 2Up,Id = UpIa.

Поскольку

Us =

имее.ч;

s 2V2

И, подставив Pd = UijId, получим: \+V.2

4]/2

Таким образом, находим, что расчетные мощности броневого и стержневого трансформаторов одинаковы. Однако стержневой трансформатор не может применяться из-за значительного одностороннего намагнячивания.

Задача 2.55. Как показано в задаче 2.54, недостатком стержневого трансформатора является значительное одностороннее намагничивание. Доказать, что одностороннее намагничивание исчезнет, если соединить вентильные обмотки по схеме зигзаг (рис. 2.108).

Решение. Для доказательства запишем уравнеяия МДС для стержня / магнитопровода

Fo-ipWp-hlWs+ialWs,

и для стержня 2 магнитопровода

Fo=ipWp-\-issWs-hlWs.

Рис. 2,108. Однофазный выпрямительный трансформатор с обмотками, соединенными по схеме зигзаг (к задаче 2.55).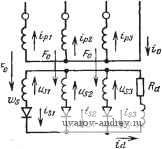

Рис. 2.109. Схема трансформатора-и вьшрямителя (к задаче 2.56).