жоммутирующих цепей и затухания циркулирующих токов, а также к расчету высщих гармоник на стороне переменного тока.

Индуктивности Lk и емкости С к, образующие коммутирующие цепи, должны выбираться так, чтобы они могли выполнять свои функции даже при наибольщих бросках нагрузки. Это условие считается выполненным, если обратное напряжение на запирающемся тиристоре поддерживается по крайней мере в течение времени, необходимом для восстановления его запирающей способности. Для данного инвертора возможно бесчисленное множество удовлетворительных сочетаний L и Ск. Оптимальное решение должно быть найдено по второстепен--ным критериям.

Проанализируем сначала коммутацию в схемах, показанных на рис. 5.1-5.7. Коммутационные процессы в этих схемах протекают одинаково [37], поэтому достаточно рассмотреть одну из них, например схему на рис. 5.1. Для упрощения анализа сделаем следующие .допущения:

пара тиристоров Ti и Tl, проводящих ток, мгновенно выключается при включении пары тиристоров Т2 и Г'г. Обратный ток в тиристорах не появляется;

тиристоры - элементы с нулевыми потерями и нулевым падением напряжения в прямом направлении;

трансформатор Тр идеальный с пренебрежимо малыми активным сопротивлением, индуктивностью рассея-.ния и намагничивающим током;

активные сопротивления индуктивностей Lk пренебрежимо малы;

на перезаряд конденсатора при коммутации не влияют обратные диоды Д1-Д4, которые остаются в закрытом состоянии во время этого процесса.

Параметры Lk и Ск рассчитываются с учетом того, что время восстановления запирающей способности тиристоров /вое и максимальный ток тиристоров во время коммутации /макс.к нормированы.

Нагрузкой инвертора может быть либо чисто активное сопротивление, либо сочетание активного сопротив-.ления с индуктивностью, либо сочетание, в которое входит противо-ЭДС. Обычно проводится анализ явления коммутации в двух экстремальных ситуациях. Во-первых, когда нагрузка - чисто активное сопротивление, т. е. ток нагрузки во время коммутации изменяется, во-

вторых, когда индуктивность нагрузки достаточно велика для того, чтобы можно было поддерживать ток нагрузки постоянным в течение всего сравнительно быстрого процесса коммутации. После выключения тиристоров Ти Т'х цепь коммутации инвертора (рис. 5.1) будет та-

Ч

L,/2

Рис. 5.11. Цепь коммутации инвертора, схема которого изображена на рис. 5.1.

Рис. 5.12. Диаграммы для расчетов цепей коммутации инверторов, работающих на активную нагрузку.

КОЙ, как показано на рис. 5.11. На тиристоры, которые прекращают проводить ток, запирающее- напряжение Обр подается от конденсатора Ск через включившиеся тиристоры Гг, Тъ Записав и решив уравнения цепи, можно вычислить время восстановления запирающей способности тиристоров вос и максимальный выброс тока i [5, 37].

Результаты обобщены в диаграммах на рис. 5.12 и 5.13. На рис. 5 12 приведена зависимость (в относительных единицах) емкости С„ и максимального выброса тока при коммутации от индуктивности Lk для 12*

Рис. 5.13. Диаграммы для расчетов цепей коммутации инверторов работающих на индуктивную нагрузку.

нагрузки, состоящей только из активного сопротивления.

Введенные относительные параметры определяются следующим образом:

и*и/Еа; i*=iR/Ed; L\=URtBoc; C*CJUc.

По графику может быть определено L к> соответствующее допустимому выбросу тока /макс.к- Затем находится значение CV- Расчетные графики для индуктивной нагрузки представлены на рис. 5.13.

Здесь введены относительные параметры

L*K=L-ijR*toc\ С'*к=?*С'к вос и /*макс.к=/макс.к >

где / - ток нагрузки во время коммутации и R*=EdlI. Процедура вычислений такая же, как при активной нагрузке.

При анализе коммутации инвертора с раздельной коммутацией (см. рис. 5.8) делается допущение о том,

что в данный момент коммутация происходит только в одной ветви. При включении тиристора Т12 проводящий тиристор Ти выключается током конденсатора, заряженного с полярностью, указанной на рисунке. Предполагается, что индуктивность нагрузки достаточно велика, и поэтому ток нагрузки / во время коммутации поддерживается практически постоянным.

Расчеты производятся по графикам, приведенным на рис. 5.14 [8] и по формуле

Во=1 сшакс/1,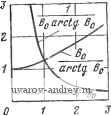

Рис. 5.14. Диаграммы для расчетов цепей коммутации инверторов с раздельным выключением тиристоров при работе на индуктивную нагрузку.

где /смакс - максимальный зарядный ток конденсатора Ск и

arctg В„ Ed

Т . dBOC j

I Во arctg

Параметры цепи коммутации обычно определяют при 5о=1. 180

процессы коммутации трехфазных инверторных схем могут быть частично сведены к процессам коммутации однофазных инверторов. Применение теории к таким случаям будет приведено в некоторых задачах.

Область применения. В инверторах нет движущихся . частей. Они быстро и легко регулируются. Все это обеспечивает им широкое и многообразное применение.

Инверторы могут с успехом применяться в качестве дополнительных источников энергии у ответственных потребителей переменного тока (телефонные станции, системы ультракоротковолновой связи, железнодорожное оборудование сигнализации и защиты и т. д.). В этих случаях инверторы предназначаются для подачи энергии переменного тока с частотой сети либо с какой-то другой частотой.

В настоящее время расширяется область применения инверторов с изменяемой частотой. Такие инверторы используются, например, для питания индукционных печей в металлургии. Инверторы с регулируемой выходной частотой используются для питания асинхронных двигателей переменного тока. Сочетание инвертора с двигателем дает возможность иметь надежные и легко регулируемые электроприводы переменного тока.

5.2. ЗАДАЧИ ЛО АВТОНОМНЫМ ИНВЕРТОРАМ

Задача 5.1. В схеме идеального однофазного инвертора ри€. 5.15) тиристоры заменены соединенными последовательно диодами и ключами. Это позволяет не рассматривать коммутационные емкость Ск и индуктивность Lk. Нагрузкой инвертора является реактор с индуктивностью L. Построить кривые токов id, i, 1д1, гд2, 1дз, im, iti,

О--

£d

. ly I

f-t

1-Ч

Т'1/f

г-д

г-д

*I naiic t

-I-ткс

гг li S 1 Ъ.

n-i-* *-

A j-AUAt-

Рис. 5.15. Схема идеального однофазного мостового инвертора (за-дача 5.1).

1т2. г'тз, T4 и напряжения и и вычислить среднее значение тока тиристора /т.ср и среднее значение тока диода /д Лп, если Ed = =10 В, L=l мГн, /=100 Гц.

Решение. Поскольку ток нагрузки обязательно протекает либо через включенные ключи, либо через обратные диоды, присоединенные встречно-параллельно ключам, включенные ключи определяют значение и полярность напряжения и. Соответственно напряжение и будет периодическим напряжением с прямоугольной формой кривой и амплитудой Еа (рис. 5.16,о). Ток i изменяется со скоростью

di , Ed dt L

Допуская, что на практике цепь всегда имеет небольшое активное сопротивление, будем считать среднее значение тока нагрузки в ивазистационарном состоянии равным нулю (рис. 5.16,6). Ток i

пропускается попеременно тиристорами и обратными диодами (рис. 5.16,е и 5-16,г). Ток, потребляемый от источника, показан на рис. 5.16,6. В инверторе и нагрузке нет потребления энергии; возникает колебание энергий между ис-Г0Ч1ШК0М и нагрузкой, как это бывает Б случае, когда индук-гивиость присоединена к сети синусоидального напряжения. Из рис. 5.16 видно, что среднее значение тока тиристора равно среднему значению тока диода и что их можно вычислить следующим образом:

- макс

-1м J - 8 ,

Рис. 5.17. Схема идеального однофазного мостового инвертора (задача 5.2).

т.ср - д.ср =

1 Т

2 4

и поско1ьку

iмякс -

di Т Еа I

макс- 4

10 0,01

4 -0- 4

=25 А,

..ср=/д.ср = 85/8 = 3,125 А.

Задача 5.2. На рис. 5.17 показана схема однофазного инвертора, в которой тиристоры заменены диодами и ключами, соединенными последовательно. Нагрузка состоит из параллельно соединенных резистора и реактора. Построить кривые токов id, t, дь *д2, (дз. д4, 1т1, 1 т2. Its. t4 и напряжения и и найти средние значения токов тиристоров и диодов, если £,(=10 В, L=l мГи, /=100 Гц и а) R=\ Ом, б) /? = 0,4 Ом, в) R = G,\ Ом.

Решение. Подобно тому, как это было в задаче 5.1, напряжение и представляет собой периодическое напряжение с прямоугольной формой кривой. Рассматривая токи соединенных параллельно ветвей нагрузки, видим, что ток через индуктивность L

имеет ту же форму, что и ток в схеме иа рис. 5.1. Его амплитудное значение может быть вычислено аналогичным способом, т. е.

£.мaкc - 4/l 4-100.10-2

-=25 А.

Ток в цепи активного сопротивления совпадает по форме с напряжением и, а его амплитуда в трех случаях будет:

Ed 10

= 10 а;

r макс

0,4 10

=25 А;

= 100 А.

Результирующий ток *= -iR-\-ib показан для всех трех случаев иа рнс. 5.18,6.

С уменьшением активного сопротивления через индуктивность проходит все меньшая часть общего тока, увеличивается интервал проводимости тиристоров (рис. 5.18,е), уменьшается интервал проводимости обратных диодов и сводится к нулю в Случаях б и в (рис. 5.18,г). Среднее значение тока, потребляемого от источника, уже не равно нулю (рис. 5.18,г). Средние значения токов тиристоров и диодов для трех рассматриваемых случаев рассчитываются следующим образом:

r=1/f

г-з

Рис. 5.18. Диаграммы характерных величин в схеме иа рис. 5.17.

а) время открытого состояния тиристоров

£макс + Iriazvc 35 о с ,г, 3

----щ-10- = 3,5.10- с;

средние значения токов тиристоров и диодов

т.ср = 2 (г.макс + Ымауис

=-3,5-10-2-35 -Jq-10= 6,125 а;

Д.ср -

2(2 (макс ~ макс) Т ~

10= 1,125 А;

=4 (5 -3,5) 10-l5-jp

б) t,=

/т.ср = 4 (макс + Wc) 4 Т =4~ + 4 = 12-5 А;

= 0;

1 Г 1

т.ср = ~2 Wrkzkc - £.макс) + (У?макс + Lыaкc) ~2~~Т~

=4 [(5° - 23) + (50 + 25)] 4~=50 А; /л.ср = 0.

Задача 5.3. На рис. 5.19 показана схема идеального однофазного инвертора, в которой тиристоры заменены диодами и. ключами, соединенными последовательно. Нагрузка состоит из ак- тивиого сопротивления R и ин- (И дуктивиости L, соединенных последовательно. Построить кривые токов id, i, 1д1, 1д2, 1дз, гд4, ti, тй, -Ed its, It4 и напряжения и и вычислить средние значения токов тиристоров и диодов, если £d=10B, L=l мГн, /?=0.4 Ом и /==100 Гц.

Рис. 5.19. Схема идеального однофазного мостового инвертора (задача 5.3).

Решение. Подобно тому как это было в задаче 5.1, напряжение и представляет собой периодическое напряжение с прямоугольной формой кривой (рис. 5.20,о). В установившемся режиме ток нагрузки имеет форму периодической кривой с амплитудами /макс в моменты t=0 и t=T/2.

Форма кривой тока описывается дифференциальным уравнением

с граничными условиями

1=-/макс при =0 и 1=/ыакс ПрИ <=7/2.

Решая дифференциальное уравнение, получаем следующую функцию для интервала 0tTI2 (рис. 5.20,6):

где r=LIR.

Подставляя <=0 и i=-/маис, получаем:

Ed l-e-/2-

шкс- 1 + е-/2

В соответствии с данными задачи при

L 10- =-=-0:4=25-10-с

максимальное значение тока равно:

, 10 1-е-

/макс- 0,4 1 + -ША.

Условие i (/;) = О определяет длительность проводящего состояния диодов:

- Jln = -2.5.10-31n -i= 1,24.10-3 с.

Среднее значение тока диода 1

Т

о

-I - /макс- HJT V - J- 0,4 10-103

10 \2,5.10-з

Среднее значение тока тиристора г/2

/ L Г (Т Л \ Г ,

10 / 10.10-

--1,24-10-

Рис. 5.21. Схема идеального однофазного инвертора (задача 5.4).

J Ш-10-

( - 16 (Т^) - - ) = 4.55, А.

Задача 5.4. В схеме идеального однофазного инвертора, представленной иа рис. 5.21, тиристоры заменены диодами и ключами, соединенными последовательно. Инвертор питает чисто-индуктивную нагрузку через трансформатор. Построить кривые токов id, i, 1д2, ill, ii2 и напряжения и и найти средние значения токов диодов и тиристоров, ЕСЛИ Ed=10 в, L=l мГн, /= = 100 Гц. Трансформатор идеальный, его коэффициент трансформации, отнесенный к одной полуобмотке, равен 1:1. Решение. Подобно тому как это было в задаче 5.1, напр-.i-жение и иа нагрузке будет периодическим с ирямоугольной формой кривой (рис. 5.22,о). Следовательно, кривая тока i будет такой же, как и в задаче 5.1. Так как исходные данные в общпх задачах одинаковые, то будут совпадать и численные значения.

Средние значения токов:

/д.ср=/т.ср=3,125 А;

/ор=0.

Задача 5.5 В идеализированной схеме однофазного инвертора, показанной иа рнс. 5.23, тиристоры заменены ключами и диодами, соединенными последовательно. Нагрузка состоит из индуктивности L. Построить кривые токов iai, id2, i, 1 д1, 1д2, 1 т1, 1т2 и напряжения и и вычислить средние зиаче-

Рис. 5.23. Схема идеального однофазного инвертора с двумя источниками питания (задача 5.5).

ния токов тиристоров и диодов, если Ed-\0 В, L-\ мГн, /=100 Гц.

Решение. Задача может быть легко решена с использованием результатов предыдущих задач. Кривые те же, что и на рис. 5.22, за исключением кривых токов источников питания, которые показаны на рис. 5.24. Численные результаты также одинаковы.

Задача 5.6. В схеме идеального трехфазного инвертора, показанной иа рис. 5.25, тиристоры заменены диодами и ключами, соединенными последовательно. Построить кривые фазных напряжений на нагрузке, токов вентилей и источника питания и вычислить средние значения токов вентилей, если £d=10 В, /=100 Гц и а) нагрузка чисто активная, Ri= =RRi=R=\ Ом, б) нагрузка чисто индуктивная, Li= =L2=L3=L= 1 мГи. Каждый ключ включается на один полупериод.

Решение. Заменим источник питания с ЭДС Еа двумя последовательно соединенными источниками с ЭДС Ел [2 каждый. Обозначим напряжения на стороне переменного тока относительно нейтрали источника питания через mio, U2o, зо> Моо- Благодаря наличию обратных диодов, соединенных встречно-параллельио с тири-.

сторами, состояния тиристоров однозначно определяют потенциалы точек 1, 2. 3 (рис. 5.26,й, б, в). Фазные напряжения получаем из уравнений

i = Uio- о'о-

Предполагая, что нагрузка состоит только из активных сопротивлений, получаем:

i; Ujr=Rk; U3=Rh,

1 + 2 + з = 10 + 20 + 30 - 3 00 = (l + 2 + з)

Рис. 5.24. Диаграммы токов источников питания в схеме на рис. 5.23.

, Поскольку

tj-K2+3=0.

Напряжение иулевой точки звезды относительно нейтрали на стороне постоянного тока показано на рис. 5.26,г. Фазные напряжения показаны пунктирными линиями на рис. 5.26,а, б, в.