Решив эти уравнения, получим fo=0, а для тока сетевой обмотки - только переменную составляющую:

(isi-is.)-

В данном случае расчетная мощность трансформатора S= =1,34Р<г, т. е. такая же, как и в задаче 2.54.

Из задач 2.54 и 2.55 следует, что для исключения нежелательного одностороннего намагничивания магнитопровода трансформатора, питающего выпрямитель с однонаправленной схемой, токи веятидьных обмоток, расположенных на каждом стержне магнитопровода, должны создавать переменную МДС.

Задача 2.56. Выпрямитель со схемой соединений ЗФШЗП присоединен к сети через идеальный трансформатор, обмотки которого соединены по схеме звезда - звезда . Выпрямитель нагружен на последовательно соединенные активное сопротивление Rd и индуктивность Ld= oo (рис. 2.109). Построить кривые токов сетевых и вентильных обмоток и вычислить расчетную мощность трансформатора с выведенной нейтралью и с изолированной.

- Решение. Сначала определим МДС в стержнях магнитопровода, пренебрегая МДС в ярмах и МДС холостого хода. Результирующие МДС в стержнях магнитопровода равны МДС одностороннего намагничивания Ро и одинаковы для всех стержней:

с

с

о

id 1 х

-cut

tJJt

Fo=Wsisi-Wpipi; Fo=Wsis2-Wpip2;

Po=WsisS-Wpip3.

Уравнение токов

P1+P2-- P3=0,

где to - ток нейтрали.

Эти четыре уравнения содержат пять неизвестных. Пятое уравнение может быть составлено на основании следующих рассуждений.

Ток через нулевой провод может протекать только в том случае, если токи сетевых обмоток содержат гармоники с номерами, кратными трем. Так как сеть дает напряжение промышленной частоты и предполагаег-ся, что трансформатор - линейный элемент, то любая гармоника в токах сетевых обмоток появляется в результате работы вентилей, присоединенных к вентильным обмоткам трансформатора. Гармоники токов вен-

Рис. 2.110. Диаграммы работы выпрямительного трансформатора щ

тильных обмоток имеют йомера!

л=ср--1 (с=0, I. 2...; р=3),

откуда пфЪк {k=\, 2 ...). и, таким образом, через нулевой провой не будут протекать токи высших гармоник. Следовательно, пятым уравнением будет го=0. Это уравнение означает также, что наличие нулевого провода не влияет на работу трансформатора. Система уравнений решается следующим образом:

S2 - 3

(- 3 + 3 3 з)

Fc = K>s

isi + is2 + S3

1±

Соответствующие крищые показаны на рис. 2.110. Расчетная мощность трансформатора вычисляется следующим образом:

/ / / /

si - S2-SS -S- y-g- ,

с; = и = г;,з = = -i;

I pi - /p2- p3 - Ip

Sp=3UpIp

fd-.

Pd = i,2iPd;

l,34Pd.

Задача 2.57. Построить кривые тока сетевой обмотки для схемы соединений, показанной на рис. 2.109, если нагрузка выпрямителя чисто активная, т. е. L(j=0. Определить влияние вывода нейтрали на стороне сети и сопоставить результаты с результатами, полученными в задаче 2.56.

7* 99

Решение. Для трансформатЬрй с Изолированной нейтраЛь16 пригодно решение, полученное в задаче 2.56:

L L \

Ра = ffi-s

isi + is2 + isi

Основная составляющая с частотой 150 Гц в односторонней МДС возникает от гармоник тока вентильных обмоток с номерами, кратными трем. Если нейтраль выведена, то через сетевые обмотки будут протекать токи нулевой последовательности, действуя как размагничивающие; цепь, через которую проходят эти токи, замкну-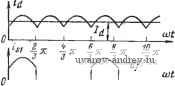

.т'1 ьг,

- Wt

Рис. 2.112. Выпрямитель со схемой ЗФШШ и трансформатором при схеме соединения обмоток треугольник - звезда (к задаче 2.58).

Рис. 2.111. Характерные диаграммы работы выпрямителя со схемой ЗФШШ, работающего на активную нагрузку, при соединении обмоток трансформатора по схеме звезда - звезда (к задаче 2.57).

та через выведенную нейтраль. В результате этого МДС переменного тока нулевой последовательности равна нулю и одностороннее намагничивание соответствует только току Id/3. Кривые токов сетевых обмоток МДС для обоих случаев показаны на рис. 2.111.

Основная роль нулевого провода состоит, таким образом, в том, что он предупреждает развитие одностороннего намагничивания на частотах высших гармоник.

Задача 2.58. Выпрямитель со схемой соединений ЗФШЗП работает на нагрузку, состоящую из последовательно соединенных резистора с сопротивлением Rd и реактора с индуктивностью Ldoo. Схема соединения обмоток преобразовательного трансформатора треугольник - звезда . Построить кривую тока сетевой обмотки и найти расчетную мощность трансформатора.

Решение. Для трансформатора, соединенного, как показано на рис. 2.112, могут быть записаны три уравнения МДС и три урав-нения токов:

Fa=isiWs-ipiWp; F(i=isiWs~ip3Wp,

и

ф2=1р2-hi, фз= рз-Р2.

Это система из шести уравнений с'семью неизвестными (токи сетевых обмоток, токи в сети и МДС F). В трансформаторе, обмотки которого соединены в звезду, сумма токов сетевых обмоток равна нулю, что может быть использовано в качестве дополнительного уравнения. В данном случае через обмотки, соединенные в треугольник , могут протекать токи нулевой последовательности, которые нам пока неизвестны. Можно сказать лишь, что из-за наличия активных сопротивлений сетевых обмоток средние значения их токов равны нулю.

Недостающее уравнение может быть записано для односторонней МДС fo, которая может быть постоянной или переменной. Однако пря соединении обмоток в треугольник может появиться МДС, противоположная по знаку переменной МДС. Магнитный поток нулевой последовательности замыкается вдоль путей рассеяния, соответственно степень компенсации односторонней МДС зависит от конструкции трансформатора. Далее будем считать, что компенсация односторонней МДС полная (т. е. односторонняя МДС не содержит переменной составляющей).

Используя это допущение, записываем интеграл

2ч

о о

МДС'в первом стержне магнитопровода Po = isiWs - ipiWp.

Имея в виду, что

11 =

2л

/jj при О < ш< <-g-;

2л

О при -g - < <о< <

2п

- 2л J

ipd(ot = 0.

находим значение односторонней МДС:

Fo=WBld/S.

1.01

Теперь Можно Достаточно просто вычислить токи сетевых обмоток:

P8= sa -Wp-[ 3 3 3 j w >

ps - - 2, ) Wp \~ 2, 3 s + 3 j a)

Эти уравнения такие же, как и для схемы соединения обмоток (задача 2.56), следовательно, и расчетная мощность трансформатора будет такой же. Односторонняя МДС, пропорциональная одной трети тока нагрузки, возникает и в данном случае.

Токи в сети

Ws . ,

- -Jr

фз- ц, ( рз - pi)-

Кривые этих токов показаны на рис. 2.113. Как н в задаче 2.56,

Ws V2 р= Wp 3 d-

В соответствии с рис. 2.113

т. е. / ф = УЪ1р.

Задача 2.59. Выпрямитель со схемой соединений ЗФШЗП работает на нагрузку, состоящую из последовательно соединенных активного сопротивления Rd и индуктивности Ld=Koo (рис. 2.114). Построить кривые токов сетевых обмоток и найти расчетную мощность преобразовательного трансформатора со схемами соединения обмоток а)- звезда-зигзаг и б)- треугольник-зигзаг .

Решение. В предыдущих задачах было показано, что расчетная мощность не зависит от коэффициента трансформации. Поэтому для упрощения примем, что Wp/Wb=1.

а) При Ws=Wp=w уравнения для схемы, показанной на рис. 2.114, будут:

Fti=w{isi-is3-hi); Fff=w (is2-i.l-рг); Fo=ro((s3-52-рз); ipi+p2-fp3=0.

Решив первые три уравнения, получим:

Fa=0,

следовательно, токи сетевых обмоток будут:

p2=s2-isi;

ipi-is3-s2-

iii.

J£/>/Ji>?JJ>3

W s Id

ЛЗ[-I I

ч1\ V

. wt

Рис. 2.113. Диаграммы работы выпрямителя на рис. 2.112.

Рис. 2.114. Выпрямитель со схемой ЗФШЗП при соединении обмоток трансформатора звезда - зигзаг (задача 2.59).

На рис. 2.115 показаны кривые, построенные на основании этих уравнений. При вычислении расчетной мощности трансформатора напряжения вентильных полуобмоток суммируем геометрически (рис. 2.116) и получим:

Is= ..глг- 1р=У ~Id,

yi ~ 1,17/3

1,171/3

s = -

Ss + Sp

Pd

2 + VT 2-1.17

1.46Prf.

6) В задаче 2.58, рассматривая трансформатор с обмотками, соединенными в треугольник, мы выя-рнили, что постоянная состав-юз

is! 2r

П П □

a) x

П П

П П П

ляющая односторонней МДС мо-cot жет быть вычислена как среднее значение МДС вентильных обмоток, расположенных на одном и том же стержне магнитопровода. Такой результат получен на осно-ujt вании предположения, с одной сто-- роны, что средние значения токов сетевых обмоток всегда равны нулю, а следовательно, и средние г) значения МДС сетевых обмоток

~[ I I wt равны нулю, а с другой, что пере---I-- --~ менная составляющая односторонней МДС равна нулю (предполагалось, что компенсация перемен-г] ной односторонней МДС полная).

1 С учетом этого, а также того, что - греднее значение pa3H0CTfi токов isi и iss равно нулю для вентильных обмоток трансформатора, показанного на рис. 2.114, получаем:

Рнс. 2.115. Диаграммы работы выпрямителя (к задаче 2.59).

Ws(isi - is3)d(ot = 0.

Отсюда видно, что уравнения токов сетевых обмоток идентичны уравнениям, полученным для схемы звезда - зигзаг . Токи сетевых

I- ФЗ

Рис. 2.116. Векторная диаграмма напряжений вентильных обмоток трансформатора на рис. 2.114.

обмоток (рис. 2.117):

Рис. 2.117. Схема для определения токов в сети (к задаче 2.59).

1ф2 = *Р2-jJI =s2-t-E3-2lsi; 1фЗ=*РЗ-fp2 = si +isi-2Js2-

Кривая тока im показана на рнс. 2.115,ж. Поскольку через обмотки, соединенные по схеме звезда - зигзаг , проходят одинаковые токи, расчетные мощности трансформаторов также одинаковы

h равйы:

S=l,46Pd. Действующие значения токвв в сети

в этом случае /ф = / 3/р, поскольку Ip=IdVV-

Задача 2.60. Выпрямитель со схемой соединений ЗФ1Н6П работает иа нагрузку, содержащую резистор с сопротивлением Rd и реактор с индуктивностью Ldoo. Построить кривые токов сетевых обмоток, определить одностороннюю МДС и расчетную мощность трансформатора. Схема соединения обмоток трансформатора: а) звезда - звезда , б) треугольник - звезда .

Рис. 2.118. Схема выпрямителя к задаче 2.60.

Sl;p1

S5;p3 I s3;pZ

Рещение. a) При Wp=Ws=w уравнения для трансформатора с обмотками, соединенными по схеме звезда - звезда (рис. 2.118), принимают вид:

fo= (s3- S6- P2); fo=B!;(Js6-J32-Jps);

Pl-fj)2+ P3=0.

Эта система уравнений имеет рещение:

ipi = -3- hi + ~ hi + 3 hs - 3 hi -

-~3~ *ss+ 3 *sei

1 1 . 2 . 1

- -3 hi + -3 S2 + 3 *S3 + 3

hi 3 hi 3 se>

- 4- hi + 4- S2 - 3 3 + 3 S4 +3 S6 + 3

*S1 - el + el - 4 + st-

Ha рис. 2.119 показаны кривые токов вентильных обмоток и построенные по ним кривые для /р, н Fo-

б) Если сетевые обмотки соединены в треугольник (см. рис. 2.117), то уравнение

Pl--tp2+pS=0,

как и в части б задачи 2.59, должно быть заменено уравнением

0- 2п

поскольку среднее значение разности токов i,i-1,4 равно нулю. Теперь легко можно вычислить токи сетевых обмоток:

pi = *S1 S4>

ps = *s - eel

ps - et - s ;

ф1 - pi *p3 = ei Ч - s4 - S6 I

- hi -\- Uz -f hi - sel

- is2 - is3 + e + se-

ф - pa - *pi ф = ps - p =

Id -ldw/3

Ha рис. 2.120 представлены токи сетевой обмотки и в сети, полученные из этих уравнений. Ниже приведен метод вычисления расчетной мощности трансформатора. Подробные вычисления предлагается сделать читателям. Следует иметь в виду, что поскольку через обмотки, соединенные в треугольник, протекают переменные токи нулевой последовательности, отношение междуфазных токов к фазным равно /з.

Рнс. 2.119. Диаграммы работы выпрямителя по схеме на рис. 2.118.

Параметры

Us Ss Ip 1ф

звезда - звезда Id

Схема соединений:

треугольник - звезда

1.35 3 d

1L.J

3 d

Ud 1.35

1,35 1.43Pd

1.35

2 ,

- Id

1,35

1,3 l,54Pd

Задача 2.61. Выпрямитель с трехфазной мостовой схемой со-сдинспий работает через сглаживающий реактор с индуктивностью Ld=oo на активную нагрузку. Найти токи сетевых обмоток, одностороннюю МДС и расчетную мощность трансформатора, схема соединений обмоток которого: а) звезда - звезда и б) треугольник - звезда .

Рис. 2.120. Диаграммы работы выпрямителя со схемой ЗФ1Н6П при схеме соединений обмоток трансформатора треугольник - звезда (к задаче 2.60).

Рис. 2.121. Трехфазный мостовой выпрямитель с обмотками грансформатора, соединенными по схеме звезда - звезда (к задаче 2.61).