Из полученных выражений для токбй следует: ток й нулевом проводе /о = / + /з + / = Ои введен только для упрощения пояснений; ток в фазе А в два раза превышает токи в фазах В и С; при этом направления токов в фазах В и С ему противоположны.

На рис. 8-14, б построены векторные диаграммы НС обмоток синхронизации датчика и приемника. Как видно из рисунка, по направлению результирующая НС совпадает с НС фазы Л, по которой протекает максимальный ток, и превышает ее в 3/2 раза. Результирующая НС обмотки синхронизации

-sin

(8-5)

Здесь щ и ko6 - число витков и обмоточный коэффициент фазы обмотки синхронизации. Разложим результирующие НС,датчика и приемника по двум осям: продольной, совпадающей с осью обмотки возбуждения, и поперечной, перпендикулярной ей. Продольная составляющая НС

е

= 1,35 Ф' (l-cosS). 2 2ф

Поперечная составляющая НС

е

Fg = Fcos-

2ф

(8-6)

(8-7)

Продольные составляющие НС датчика и приемника направлены навстречу НС обмоток возбуждения. Поперечные составляющие НС образуют поперечные магнитные потоки. При малых углах рассогласования продольная составляющая НС значительно меньше поперечной. Например, при 6 = 5°

1 - cos 5° sin 5°

= 0,026.

Аналогично можно ввести понятие о продольном и поперечном токах, подразумевая под этим такие уравнительные токи, которые создают продольную и поперечную НС:

- /л sin 4- = 4 (1 - cos в); (8-8)

sin е. (8-9)

На рис. 8-15, а приведена векторная диаграмма токов и напряжений для продольной оси датчика. Продольный магнитный поток и ток /о совпадают по фазе. ЭДС в цепи синхронизации 2 sin (9/2) и ЭДС обмотки возбуждения отстают по фазе от магнитного потока на 90°. Ток отстает от ЭДС на угол щ, который

г в

/cos -=

2ф 3 £ф

определяется активной и реактивной частью сопротивления 2ф. Первичный ток if равен сумме тока холостого хода и приведенного продольного тока Id, идущего на компенсацию размагничивающего действия продольной НС. Сумма противо-ЭДС - Ef w падений напряжений на активной и реактивной составляющих сопротивления обмотки возбуждения равна приложенному напряжению. Как видно из рис. 8-15, а, векторная диаграмма по продольной оси сельсина аналогична векторной диаграмме двухобмоточного трансформатора, в котором роль тока нагрузки выполняет продольный ток цепи синхронизации.

На рис. 8-15, б приведена векторная диаграмма для поперечной

ZEcpSinj-

в

Рис. 8-15. Векторные диаграммы сельсина-датчика: а - для продольной оси; б - для поперечной оси

ОСИ сельсина-датчика. Поперечный ток имеет ту же фазу, что и продольный ток id, так как они являются проекциями одного и того же тока на поперечную и продольную оси. Поперечный магнитный поток совпадает по фазе с током При малых углах рассогласования уравнительный ток в цепи синхронизации имеет максимальное значение в фазе А, ось которой почти совпадает с поперечной осью, и вся обмотка синхронизации создает в основном поперечную НС. Поэтому под сопротивлением 2ф, которое использовалось в уравнениях (8-6) - (8-9), следует понимать полное сопротивление фазы при совпадении ее оси с поперечной осью. Как известно из теории синхронных машин, это сопротивление называется поперечным сопротивлением фазы и обозначается Z.

Найдем выражение для момента. Оно получается как разность моментов создаваемых взаимодействием продольного магнитного потока с поперечным током и поперечного магнитного потока с продольным током:

M=¥d/ cos(4rf, g-¥,/rfCOs(¥ Id).

(8-10)

Здесь ¥d и - потокосцепления фазы, создаваемые магнит-

ными потоками Ф</ и Ф

При малом угле рассогласования Id Ig и вторым членом в этой формуле можно пренебречь. Из векторной диаграммы на рис. 8-15, 6 ясно, что

С05(ЧО,) - sin {Elg) = Xg/Zg. (8- l l)

Подставляя выражения (8-9) и (8-11) в формулу (8-10) и учитывая, что Еф = ¥(0, получаем (в ньютон-метрах)

i: sin fl

(8-12)

(8-13)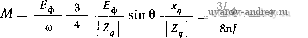

Удельный синхронизирующий момент (в Н-м/рад)

dQ е=о 8я/ r + xl

Для получения удельного синхронизирующего момента в Г-см/ . . .° выражение (8-13) надо умножить на множитель --. В результате получим

180/я (8-14)

Это одна из основных формул теории индикаторной синхронной передачи.

8-3. Зависимость удельного момента от параметров сельсина. Особенности устройства сельсинов

Формула (8-14) показывает, что при заданных частоте сети и магнитном потоке Фа, определяющим фазную ЭДС, удельный синхронизирующий момент существенно зависит от соотношения между параметрами Гд и Хд. Удельный момент имеет наибольшее значение, если Хд Гд, т. е. индуктивное сопротивление фазы по поперечной оси равно ее активному сопротивлению. Для получения необходимого значения Хд при конструировании сельсина применяются два способа: 1) уменьшение полюсной дуги в явнополюсных сельсинах; 2) размещение на роторе короткозамкнутого демпферного контура вдоль поперечнойоси для явнополюсных и неявно-полюсных сельсинов. Щ -Ч

При реализации этих способов надо иметь в виду следующее. Уменьшение полюсной дуги приводит к падению основного магнитного потока и, следовательно, ЭДС фазы и синхронизирующего момента. Демпферный контур по поперечной оси должен быть установлен таким образом, чтобы не демпфировать продольного магнитного потока. Следует также отметить, что такой демпфер-

Рнс. 8-16. Схема для определения параметров фазы сельснна по поперечной осн

НЫЙ контур приводит к увеличению активного сопротивления фазы по поперечной оси г'д. При наличии демпферного контура полное сопротивление фазы по поперечной оси определяют, исходя из схемы замещения, приведенной на рис. 8-16. Положительным качеством демпферного контура, кроме уменьшения х'д, является ускорение затухания колебаний при согласовании сельсинов (см. § 8-6). Поэтому выбор оптимального демпферного контура и его параметров представляет собой довольно сложную задачу.

В явнополюсных сельсинах демпферный контур выполняется в виде короткозамкнутого витка 2, плоскость которого совпадает с направлением основного магнитного потока (рис. 8-17). У неявно-полюсных сельсинов обмотка ротора выполняется двухфазной или трехфазной. При двухфазном исполнении одна из фаз является обмоткой возбуждения, а перпендикулярная ей фаза - демпферной обмоткой. При трехфазном исполнении фазы соединяются

согласно схеме, приведенной на рис. 8-18. Нетрудно видеть, что при такой схеме включения все фазы выполняют функции демпферного контура, так как они замкнуты накоротко по отношению к поперечному магнитному потоку.

В бесконтактных сельсинах конструкции Иосифьяна-Свечарника специальный демпферный контур отсутствует, его функции выполняют листы стали ротора, перпендикулярно которым замыкается поперечный магнитный поток (рис. 8-19). Попутно обратим внимание на одну особенность листов пакета статора 7 и кольцевых магнитопроводов 1 в этих сельсинах (см. рис'8-5). Поотноше-потоку они являются коротко-вызвать нежелательный нагрев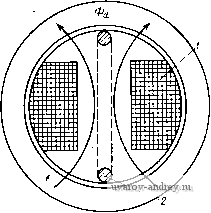

Рнс. 8-17. Демпферный контур в яв-нополюсном контактном сельсине

/ - обмотка возбуждения; 2 - демпферная обмотка

нию к продольному магнитному замкнутыми витками, что может пакетов статора и кольцевых магнитопроводов. Для исключения этого явления листы стали делают разрезными (рис. 8-20). При веерной сборке пакетов и торов это не нарушает их механической прочности,

в заключение настоящего параграфа рассмотрим зависимость удельного синхронизирующего момента от частоты сети. Учитывая, что

£ф = 4,44Ф^Шф.зф и х^==2л!ХУф.,ф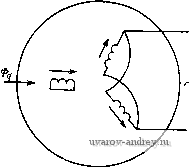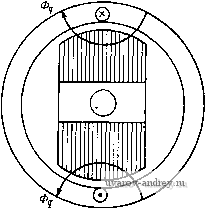

Рис. 8-18. Образование демпферных контуров и обмотки возбуждения из трех фаз ротора

Рис. 8-19. Демпфирование поперечного магнитного потока в бесконтактном сельсине Иосифьяна-Свечарника

(где Шф. эф - эффективное число витков фазы синхронизирующей обмотки; \ - магнитная проводимость по поперечной оси), фор-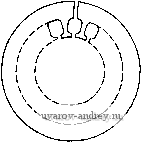

Рнс. 8-20. Листы пакетов стали ротора н кольцевого магнитопровода бесконтактного сельсина

мулу (8-14) запишем в виде

где = 66,6/\.

Из полученной формулы на первый взгляд следует, что при увеличении частоты удельный синхронизирующий момент всегда растет; на самом деле это не совсем так. По условиям теплового

режима с увеличением часюты необходимо уменьшать магнйТны) поток, поэтому зависимость удельного момента от частоты оказывается связанной с габаритами сельсина.

Рассмотрим сельсины различных габаритов, спроектированные для работы на промышленной частоте. Данные расчета, а также ранее выполненные образцы сельсинов показывают, что при диаметре корпуса Dk<40 мм и г'д >Хд тепловой режим в машине в основном определяется потерями в обмотке возбуждения; при Dk>60 мм оказывается, что rq < jc и на тепловой режим существенное влияние оказывают потери в стали.

Поэтому в малогабаритных сельсинах с ростом частоты магнитный поток практически остается постоянным, а отношение rqixq уменьшается, что приводит к увеличению удельного синхронизирующего момента; в сельсинах относительно больших габаритов с ростом частоты необходимо уменьшать магнитный поток; в результате удельный синхронизирующий момент будет падать.

Из приведенных рассуждений следует, что для данного габарита существует оптимальная частота, при которой характеристики сельсина оказываются наилучшими. Поскольку при проектировании сельсинов представляется возможным варьировать многие его размеры (диаметр расточки, полюсная дуга, воздушный зазор) и параметры демпферного контура, то для каждой из частот, предусмотренной ГОСТ, можно получить вполне удовлетворительные по характеристикам, сельсины в некотором интервале габаритных размеров. Так, например, сельсины промышленной частоты проектируются в корпусе диаметром от 50 до 100 мм, а сельсины повышенных частот (400-500 Гц) - диаметром от 25 до 50 мм.

8-4. Точная теория индикаторной синхронной передачи при однотипных датчике и приемнике

Схема парной синхронной передачи в индикаторном режиме с сельсинами, трехфазные обмотки которых приведены к эквивалентным двухфазным, показана на рис. 8-21. Обозначая индексом 1 величины, относящиеся к датчику, а индексом 2 - к приемнику, составим уравнения ЭДС датчика и приемника в соггветствии с формулами (1-23):

(8-15)

Поскольку к обмоткам d и Я наПрйжеМиё йе йоДвоДиТся, То

Udi = Ud2 = Ugl = Ug2 = 0.

Выражение для момента сельсина-приемника находится по правилам приведенным в § 1-2:

М = Re {bJ,) , 2й)

где /j-вектор тока сельсина-приемника; Sj - обобщенный вектор индукции, составляющие которого равны коэффициентам при v в уравнении ЭДС приемника (8-15). Множитель обусловлен тем фактом, что в сельсинах синхронизирующая обмотка является трехфазной.

Г

? Of

Рнс. 8-21. Схема парной синхронной передачи в индикаторном режиме, приведенная к осям dug

Развернем формулу момента:

Re [/Еф/г + Xi (DldJqi ~ Хд {,1)1дгЦЛ-

(8-16)

Соединение обмоток датчика и приемника по схеме, приведенной на рнс. 8-21, можно рассматривать как преобразование токов с матрицей преобразования

Используя формулы (1-28) и (1-29), из уравнений (8-15) получим

2r + j[Xd(i)(\ + cod) + + Xg(i)smQ\+v[xd{i)-

- Xq (/)] sin 6 COS e

-i{xd(i)-xq (/)] sin e COS e+

+ v{xd(i)(\+fosQ) + + Xg(i)sm4\

- i \xd (I)-Xg (/)] sin e COS e -

-v[Xg(j)(l + cosQ) + + Xd (/) sin 6]

2r+i[Xg(j)(l+cosQ)-

+ XdU)sin Q]-V[Xd(j)-

- }ig (/)] sin e COS e

Ёф (1 - cos 0) + /Ъ£ф sin 9

(8-17)

Решение э*нх уравнений в общем биДё при любом угле рассогЛаёобаййЯ 6 и относительной угловой скорости сельсинов v представляет значительные трудности и поэтому нецелесообразно.

Рассмотрим два частных случая; имеющих практический интерес.

1. Режим синхронного поворота (v = 0). В этом случае решение уравнений (8-17) относительно токов Id и Ig получается сравнительно просто и имеет вид:

/d = -(l-cose); Z

* Z

где

Z = 2г + jxd (/) (1 - cos 6) + jxg U) (1 + cos 6). Подставляя токи в формулу момента (8-16), получаем

М =-2 х

Х

х^ sin I

d + h

coseJ + (

х^ - х„

cose)

(8-18)

Здесь rd + jx, = г + jxd (,), г'д+Уд = г + \хд (/) представляют со-бой параметры фазы синхронизирующей обмотки по продольной и поперечной осям с учетом электромагнитного взаимодействии фазы с обмотками возбуждения и демпферной.

Из формулы (8-18) можно получить удельный синхронизирующий момент (в Н.-м/рад)

в=о

Гд -YXg

ИЛИ (в Г-см/ . . .°)

= --ч

г'А- х'

Гд -t Хд

(8-19)

(8-20)

Фазные токи в цепи синхронизации находим как проекции векторов Id и / на осн соответствующих фаз. Так, например, для фазы Л получим

= /rfcos ttn + /sinon = [(1 - cos 6) cos an + sin 6 sin ] (8-21)

Ток фазы синхронизирующей обмоткн зависит от угла рассогласования 6 и от положения осн фазы относительно обмоткн возбуждения. При расчетах целесообразно учитывать максимальное значение тока, которое, как это

я 6

следует нз (8-21), получается при = -----

/А

о

- 9 ~ С1

2. Режим сййхройной скорости (о = 1). Решая урайнеййя (8-17) при V - I, находим .

j £ф(1 - cos6 + /sin6)

£ф{5ш9 -/(1 - cos9)l 2 [г+ №(/) +/ ,(/)]

(8-22)

Прн синхронной скорости ротора токи синхронизирующей обмотки сельсина образуют круговое вращающееся магнитное поле двойной частоты по отношению к частоте напряжения возбуждении. Действительно, комплексный временной вектор тока фазы А

(О = ( / cos а„ + / sin а„) е^ = / e-le п = /е'2 ,

iM/Mo п = 0); = - rf.

Подставляя выражения (8-22) в формулу момента (8-16), получаем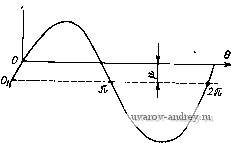

40) *

(rf + \) sin е - г(1 - COS 6)

Рис. 8-22. Кривая синхронизирующего момента сельсина-приемника в относительных единицах при v = 1

или, после некоторых преобразований.

где

V(rf+<)4r sin (е-Ьф)-г

= Mo [sin (6 + ф') - ,1],

(8-23)

Л1 =-

Кривая синхронизирующего момента, выражаемая формулой (8-23), представляет собой синусоиду и изображена в относительных единицах иа рис. 8-22.

8-5. Некоторые специальные режимы работы индикаторной синхронной передачи

Среди различных режимов работы индикаторных синхронных передач практический интерес представляют: параллельная работа однотипных сельсинов-приемников от одного датчика, парная синхронная передача при

фазовом сдвиге между напряжениями датчика и приемника, система синхронной связи с электрическим дифференциалом. Ниже рассматриваются основные соотношения для перечисленных режимов.

Параллельная работа сельсинов. Электрическая схема синхронной передачи при работе п однотипных сельсинов-приемников от одного датчика приведена на рис. 8-23. Здесь синхронизирующие обмотки сельсинов заменены эквивалентными двухфазными обмотками по осям d и д. Примем, что фазные ЭДС датчика и приемника одинаковы, а угол рассогласования 6 мал. Тогда для цепей синхронизации получаем простые уравнения ЭДС.

(Zrfi + Zrfa) /rf = £ф (1 - cos 6) 0;

(Zgiti + Zgi) lg = £ф sin e £фв.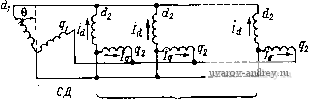

71 - приемников

Рис. 8-23. Схема параллельной работы сельсинов в индикаторном режиме, приведенная к осям d и q

/rffeO;

ёфб

Zgn + Z.

Подставляя эти токи в формулу для момента сельсина-приемника (8 16), получаем

3 -/

2со *

Заменяя Zgi на ri+jxgi и Zg на / ,2 +/,2. находим 3£фв xgin + xg2

{гдп + /,У+{х1,п+х',у Отсюда удельный синхронизирующий момент

3£

2 {rgn+rg,Y + {xg,n + x,У

(8-24)

Формула (8-24) переходит в полученное выше выражение (8-19), если датчик и приемник однотипны, а я = 1.

Парная синхронная передача при фазовом сдвиге между напряжениями датчика и приемника. Для выяснения влияния фазового сдвига между напряжениями датчика и приемника на работу индикаторной синхронной пе-

редачи рассмотрим наиболее простой случай: параметры сельсинов по продольной н поперечной осн одинаковы. Для сельсинов, имеющих демпферные контуры, это условие выполняется достаточно точно. Тогда выражение для токов в контурах d п q (см. рнс. 8-21) прн условии, что напряжение возбуж

дения датчика Uf~, запишем в виде

. £ф(1-со8ее-/Р) . £ф8шее->

2[г + ;\(/)1 2[г+/,(/)1

Подставляя этн выражения в формулу (8-16), получим синхронизирующий момент приемника

3 / cos ф + г' sin ф М = -- filsinG ----:-.

(8-25)

Выражение для момента датчика получается нз этой формулы путем замены угла ф на - ф:

3 ;t cosф-гsiпф М =-£isin 9 ----

(8-26)

Из приведенных формул следует, что, если напряжение возбуждения приемника опережает по фазе напряжение возбуждения датчика, сннхро-ннзнрующнй момент прнеминка растет, а момент датчика падает. В частно-

стн, прн tg ф = -2- момент датчика становится равным нулю, а синхрони-

зирующий момент приемника

ч х„ cos ф

М=~е2 sin9-2--

20) * r}jx

(8-27)

ч

Этн свойства системы синхронной передачи получаются за счет уравнительных токов в цепн сннхроннзацин прн согласованных датчике и приемнике. Максимальный фазный ток

/ Еф sin (ф/2)

ф. макс - -

2 + д:2 9 T-t,

(8-28)

Указанные свойства синхронной передачи необходимо учитывать при проектировании индикаторных синхронных передач с длинными линиями связи, в которых за счет падения напряжения в кабеле возникают существенные фазовые сдвиги в напряжениях возбуждения датчика и приемника.

Система синхронной свизн с электрическим дифференциалом. Принципиальная схема синхронной передачи с электрическим дифференциалом (ЭД) н двумя однотипными датчиками, синхронизирующие обмотки которых приведены к осям du q, изображена на рнс. 8-24. Будем считать, что выходные сопротивления сельсннов-датчиков по продольной и поперечной осям одинаковы, = Zl = 4-/л:, так же как параметры обмоток статора и ротора электрического дифференциала. Последнее допущение связано с тем, что прн проектировании ЭД коэффициент трансформации его обмоток выбирают равным единице с целью получить одинаковые намагничивающие токн датчиков. Примем также, что угол рассогласования 9 мал. В этом случае уравнения ЭДС синхронной передачи по осям d q незавнснмы друг от друга и имеют вид

- Ёф -Еф sin (9/2)

Еф sin (9/2)

(8-28)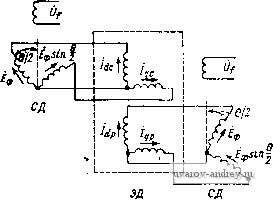

Рис. 8-24. Система синхронной передачи с электрическим дифференциалом, приведенная к осям d и q

Здесь Zi = rq + jxg+ ri+ / is - ропротивленне цепн синхронизации, включающее в себя выходное сопротивление сельсина-датчика и сопротивление собственных параметров обмоток ЭД; сопротивление взаимной индукции обмоток ЭД.

Решая уравнения (8-28) относительно токов, получаем:

= Ыр - -

Zi+2ix

Iqc= -1чР = -TSln 1

(8-29)

Выражение дли синхронизирующего момента ЭД на основании формулы (1-17) запишем в виде

- Re(/rfc/<,p-/9 Jdp)-

Подставляй сюда ЛоЯуЧеййые вЬше выражения дЯя toKoB, ваходим

£Re-

- sin -

sin -

(8-30)

Введя относительные параметры

q + ri

= X,

получим известную формулу удельного синхронизирующего момента ЭД [23]

rq + r,

ОЛ 0,6 OJB 1,0 1,2 Рис. 8-25. График функции F (ху)

F(x, у),

(8-31)

где

F(x, у) = 4х-

1 + (У + 2х)у

1\+(у + 2хП(1 + у^)

представляет собой безразмерную функцию, графики которой для различных X приведены на рис. 8-25.

Наибольший намагничивающий ток в цепн синхронизации определяется из первого выражения (8-29).

ф. макс -

£ф

rq + r,

yi + (y + 2xf

(8-32)

8-6. Демпфирование колебаний сельсина-лриемника при согласовании

Система синхронной передачи в индикаторном режиме может с успехом выполнять свои функции, если переход от одного угла поворота к другому происходит достаточно быстро, без значительных колебаний ротора приемника. Поскольку синхронизирующий момент приемника пропорционален углу рассогласования, а ротор приемника вместе с указателем имеет определенный момент инерции, то при быстрых изменениях положения ротора датчика неизбежны колебания ротора приемника около нового положения согласования. Для быстрого затухания этих колебаний сельсины снабжаются демпфирующими устройствами. Наибольшее распространение имеют два способа гашения колебаний: внутреннее электромагнитное демпфирование с помощью специальных коротко-замкнутых контуров, размедаемых вдоль поперечной оси сельсина,

и внешнее демпфирование - магнитоэлектрическое и механическое. Следует также отметить, что на характер затухания колебаний ротора приемника оказывает влияние сухое трение в подшипниках и между контактными кольцами и щетками.

В общем случае при обоих видах демпфирования дифференциальное уравнение движения ротора приемника при малых колебаниях около положения согласования имеет вид

= -mQ-To

dQ rp da

(8-33)

Здесь Td dbldt - демпферный момент за счет внутреннего демпфирования; То icfan/d - демпферный момент от внешнего магнитоэлектрического демпфера; Mj - момент сухого трения; /р- момент инерции ротора приемника.

Если принять за начало отсчета угла поворота роторов датчика и приемника положение согласования, то = 9 и уравнение (8-33) примет вид

+ {То Л- Tdi) - + тВ = ±Мгр.

Разделив правую и левую части уравнения на /р, получим

9 +2X0 + vg(0±e.,p) = O,

(8-34)

где Я, = (То -Ь Го1)/(2/р) - коэффициент затухания колебаний, обусловленный внутренним демпфированием и внешним магнитоэлектрическим демпфером; Vo = YmlJp - угловая скорость свободных колебаний; 9ip = Mrplm - зона нечувствительности, определяемая моментом сухого трения и удельным синхронизирующим моментом.

Решая уравнение (8-34), получим формулу для определения времени затухания при некотором начальном малом угле рассогласования [231:

-(1-е)

(8-35)

где О = е- - декремент затухания колебаний.

Время затухания колебаний определяется главным образом коэффициентом затухания к, который зависит от постоянных внутреннего и внешнего демпфирования То и Toi.

Для выяснения физической природы внутреннего демпфирования рассмотрим режим малых качаний приемника около согласованного положения. В этом случае трехфазную обмотку синхронизации можно заменить фазой q (рис. 8-26). При качаниях ротора приемника его магнитный поток возбуждения индуцирует в обмотке синхронизации кроме трансформаторной ЭДС еще^ЭДС вращения, пропорциональную угловой скорости ротора. Частота ЭДС вращения равна частоте сети. Под действием этой ЭДС в nonq)e4HOM

контуре сельсина возникают добавочные токи. Эти токи индуцируют в короткозамкнутых контурах датчика и приемника токи, что приводит к превращению электромагнитной энергии, запасенной в контуре q за счет вращения ротора, в тепло, выделяемое в ко-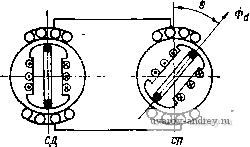

Рис. 8-26. к пояснению физической природы внутреннего демпфирования сельсинов

роткозамкнутых контурах. Нетрудно видеть, что короткозамкнутые контуры датчика и приемника выполняют одинаковую роль в создании демпферного момента.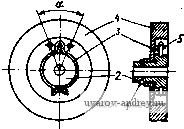

Рис. 8-27. Конструкции механического инерционно-фрикционного демпфера

/ - стопорное кольцо; 2 - втулка; 3 - фрикционное устройство; 4 - маховое колесо 5 - упоры

Рис. 8-28. Конструкция электромагнитного демпфера

/ - внешний магнитопровод; 2 - полый ротор; 3 - постоянный магнит

Постоянная внутреннего демпфирования определяется параметрами сельсинов по поперечной оси и при работесельсина-приемника от однотипного датчика находится по формуле [231

Api (:±!q)OZ-4) + 2V>o 1

(8-36)

где Го и - парам.егры, зависящие от сопротивлений демпферного контура сельсина.

Как видно из формулы (8-36), с увеличением частоты сети эффективность внутреннего демпфирования резко падает, поэтому 220

в синхронных передачах на повышенных частотах применяют внешние магнитоэлектрические или механические демпферы, принципиальные конструктивные схемы которых приведены на рис. 8-27 и 8-28. . Ы

Для определения постоянной демпфирования магнитоэлектрического демпфера заменим полый ротор короткозамкнутой обмоткой с некоторым эффективным числом витков аУэф- Магнитный поток, сцепляющийся с обмоткой, при качаниях ротора с амплитудой Оо и частотой Vo

Ф = Ф„ео5шрго; соответственно этому ЭДС

,е=- ШэфФтбоРО cos pV =-Em cos pvj.

средняя мощность, рассеиваемая в роторе, при условии, что с^о-проТивление ротора принимается чисто активным, находится по 4юрмуле

т

2г

(8-37)

где г - приведенное к короткозамкнутой обмотке сопротивление полого ротора. Оно определяется по формуле [19]

4 /Ал 2

где относительный вылет лобовой части ротора k = l ll.

Эта мощность покрывается за счет механической мощности качаний ротора, среднее значение которой за период

К = То1(ШЩ=Тв1&Уо/2. (8-38)

Приравнивая друг другу правые части (8-37) и (8-38), получаем

или, подставляя = Bg Dl/p, находим

--Вб-г-

4 pk

(8-39)

Затухание колебаний при наиболее распространенном двухступенчатом инерционно-фрикционном демпфере, изображенном на рис. 8-27, носит сложный характер и в силу нелинейности задачи не поддается расчету. Обычно такие демпферы настраиваются на оптимальные, условия затуханияэкспериментальным путем.

8-7. Погрешности индикаторной синхронной передачи

Синхронизирующий момент сельсина-приемника пропорционален углу рассогласования и в согласованном положении датчика и приемника равен нулю, поэтому наличие даже самого незначи-

тельного тормозного момента, приложенного к ротору приемника, приводит к некоторой погрешности в синхронной передаче. Для определения погрешности составим дифференциальное уравнение движения ротора приемника

Ур=Мз(е, ё, v) + Mr{a an), (8-40)

где Ms (6, б, v) - электромагнитный момент, возникающий на роторе приемника вследствие взаимодействия токов и магнитных потоков в системе синхронной передачи; при малых углах рассогласования и сравнительно небольших скоростях, типичных для индикаторных синхронных передач, Мэ = - тд-Т^ dQIdt; My (an, ttn) - тормозной момент на валу приёмника, обусловленный трением в подшипниках и щетках, неточностью балансировки ротора и указателя, асимметрией магнитной цепи и наличием короткозамкнутых витков, зубцовыми пульсациями магнитного потока, внешним магнитоэлектрическим или механическим демпфированием.

В индикаторных синхронных передачах различают погрешность двух видов: статическую и динамическую. Статическая погрешность определяется в режиме поворота (ад = 0) из уравнения

или при малом угле рассогласования

е=Мт(ап)/т. (8-41)

Тормозной момент приемника в режиме поворота может быть записан в виде [23]

Mr (an) = ±Mrp + Мнеб sin (an + щ) + Mr sin (2an + a) +

--Msin(2na -t-a,), (8-42)

где Mrp - момент сухого трения; Мнеб - максимальный момент от небаланса ротора и указателя; Mr - максимальный реактивный момент от электромагнитной асимметрии магнитопровода приемника; Мг - максимальный момент от зубцовых пульсаций магнитного потока.

Формулы (8-41) и (8-42) дают приближенную зависимость статической погрешности сельсина-приемника от углового положения ротора и позволяют по экспериментально снятой кривой погрешностей определить, какой из факторов, влияющих на погрешность, является наиболее существенным. Так, например, если кривая погрешностей имеет^два'периода изменения за один оборот ротора приемника (рис.8-29), то главное влияние на погрешность оказывает электромагнитная асимметрия магнитопровода.

В зависимости от максимальной статической погрешности (от ± 30 до ± 90) индикаторные синхронные передачи делят на четыре класса точности.

Динамическая погрешность индикаторной синхронной передачи определяется при вращении ротора датчика по заданному закону обычно принимается синусоидальный закон движения с некоторой амплитудой а^т и угловой частотой Q.

Оценим динамическую погрешность для случая, когда тормозной момент на валу приемника равен нулю. Уравнение (8-40) запишем в виде

Подставляя Сюда an-a = 9 и ад = a cos получаем

рё -Ь {Td + Tdi) e + mQ=- JpO.mQ cos Q-Тшдт sin Qt.

Разделив правую и левую части на Jp и введя обозначения {Td + TdiVJp = 2 и ToiUp = 2i> получим уравнение вынужденных колебаний ротор а-приемника в канонической форме

, ё +2X6-1-vo=-

= - адО (Q cos -Ь 2Xi sin Qf).

Рис. 8-29. Кривая погрешности сельсина-приемника от асимметрии магнитопровода статора

Отсюда для максимальной погрешности сельсина-приемника в динамическом режиме получаем формулу

[(q2 v2)2 + 4).2Q2-1/2

(8-43)

По этой формуле для заданной динамической- погрешности можно определить допустимый коэффициент затухания к^ внешнего магнитоэлектрического демпфера.

8-8. Теория трансформаторной синхронной передачи

Принципиальная схема трансформаторной синхронной передачи на сельсинах, трехфазные обмотки синхронизации которых приведены к осям, d и (7, изображена на рис. 8-30. Уравнения ЭДС датчика и приемника до соединения их обмоток синхронизации и поворота ротора датчика от согласованного положения на угол 9 имеют вид:

dl (7i rfa

92

ri + IXdl U) VXdl U) 0

<7i

- VXgl (j) n -f jXqi (/)

ri + ixdi. U) vxd-i (/)

<72

- VXgi

(8-44)

В этих уравнениях индексом 1 обозначены параметры датчика, а индексом 2 - параметры приемника; прн этом параметры приемника по поперечной осн не являются переходными (см. § 1-3), так как трансформаторный сельсин-приемник не содержит поперечного демпферного контура. При определении операторного сопротивления приемника ха (/) следует иметь в виду, что к параметрам управляющей обмоткн сельсина-приемника Tf2 + ixf2 добавляется сопротивление нагрузки

= --/

+ IXh + Zh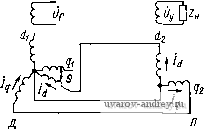

Рис. 8-30. Схема парной синхронной передачи в трансформаторном режиме, приведенная к осям d и q

Для перехода к ЭДС трансформаторной синхронной передачи выполним преобразования токов с помощью матрицы преобразования в соответствии с рнс. 8-30:

Выполняя преобразования по формулам (1-30), получаем

ri-hr2+ilxdiU)smQ + + л:,1(/)соз2е + л:2(/)]-- V [xdiU) - K<?i(/)}sinecos 6

/[A;</i(j)-A;<?i(/)lsinecose-i-

+ vlxai (Osine-b

+ XgiU)C0Se + Xa2U)]

i [Xdl U) - Xqi (/)] sin e cos 6-

-v[xaiU)cosQ + + XgiU)5inQ+Xg,]

ri + r2 + i[xdi{i)cose + + Xqi(i)s\nQ + Xq,] + + V [xdi (/) - XgiU)] sin ecos (

Яф(81пе-

Jg J L Яф(С03е-

jv COS e)

-/fsine) .

(8-45)

Из полученных уравнений для любых значений параметров датчика и приемника, угловой скорости сельсинов и угла рассогласования О можно найти продольный ток приемника /2 = Id, а затем и напряжение на управ-

ляющей обмотке по формуле

jXmdJ d

rf2 + /а:/2 + 2н

Рассмотрим решение уравнений (8-45) для ряда частных случаев. Режим синхронного поворота при малом угле рассогласования (v = О, е < зг/2). Уравнения (8-45) примут вид

Решая этн уравнения относительно токов и Ig, получаем

!q =

{Г1 + Г2+ i [xqi 0) -f Хдз]} Ёф Sin e

in +Г2 + 1 [Xgl (/) + Xd2 (/)] ]{Г1+Г2+! [Xdl (/) + Хдё ]

Ёф

Г1 + Г2 + i [Xdl (/) -f Xgi]

(8-46)

Формула тока Id несколько упрощается, если сельснн-датчнк обладает равными параметрами по продольной и поперечной осям, т. е.

id =

Ёфз1п е

ri+r2 + i[xdl(i) + Xdi(j)]

Режим вращения с малой скоростью при симметричном датчике и малой угле Q(xdi (/) = Xgi (/)). Уравнения (8-45) запишутся в виде

dr Г1 + Г2+ -vlxdi{j) + .

+ i [Xdl (/) + Xd2 (/)] V [Xdl (/) + Xd2 (/)] ri -b Г2 -f

Ёф(з1пе-1-

-- jv COS 6)

£ф(соз e - -/i sine)J

Id =

Ig =

Отсюда для токов Id и Ig находим: Ёф

ri + Г2+ i lxdi{i) + Xd2ii)]

n+ri + ilxdi Ц) + х,

jsin

/(ri-f r2)C0Se

-(cos e -

q2] I

ri + r2 + ilXdlU) + Xd2(i)]-

iv{ri + r2)sine \

ri + ri + jlXdiU)+Xq2] )

(8-47)

Полученные выражения показывают, что при малом угле рассогласования Ток /д (намагничивающий ток в цепи синхронизации) не зависит от скорости. В токе id появляется составляющая, пропорциональная относительной скорости, которая обусловливает скоростную погрешность (см. § 8-9).

8 Заказ № 678 225